Fourier Transform Properties, Aplicações, Exemplos

O transformada de Fourier É um método de adequação analítica orientada para funções integráveis ​​que pertencem à família de tRansformado abrangente. Consiste em uma redefinição de funções F (t) em termos de cos (t) e sen (t).

As identidades trigonométricas dessas funções, juntamente com suas características de derivação e antiderivação, servem para definir a transformação de Fourier através da seguinte função complexa:

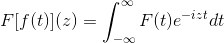
Que é cumprido enquanto a expressão faz sentido, isto é, quando a integral imprópria é convergente. Algebricamente, diz -se que a transformação de Fourier é um homeomorfismo linear.

Qualquer função que possa ser trabalhada com a transformação de Fourier deve apresentar a nulidade fora de um parâmetro definido.

[TOC]

Propriedades

Fonte: pexels

A transformação de Fourier atende às seguintes propriedades:

Existência

Para verificar a existência da transformação de Fourier em uma função f (t) definida no Royals R, Os 2 axiomas a seguir devem ser atendidos:

1. f (t) é contínuo em pedaços para tudo R
2. f (t) é integrável em R

Linearidade da transformação de Fourier

Seja m (t) e n (t) duas duas funções com Fourier definido transformado, com constantes a e b qualquer.

F [a m (t) + b n (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)

Que também se baseia na linearidade da integral de mesmo nome.

Fourier transformado de um derivado

Você tem uma função F  que é contínuo e integrável em todos os reais, onde:

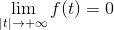
E o derivado de F (f ') É contínuo e definido em pedaços em tudo R

A transformação de Fourier de um derivada é definida pela integração por partes, pela seguinte expressão:

F [f '(t)] (z) = izF [f (t)] (z)

Em derivações de ordem superior, será aplicado de maneira homóloga, onde para todos os n 1 você deve::

F [f ⁿ'(t)] (z) = (iz)ⁿF [f (t)] (z)

Diferenciação da transformação de Fourier

Você tem uma função F  que é contínuo e integrável em todos os reais, onde:

Eu (d/dz)F [f (t)] (z) = F  [T .  f (t)] (z)

Fourier transformado de uma tradução

Para tudo θ que pertence a um conjunto e T que pertence ao conjunto S ', você precisa:

F [ τ_para θ] =  e^-IAY F [[ θ]                                 F [ τ_paraT ] =  e^-IAX  F [[ T]   

Com  τ_para  trabalhando como operador de tradução no vetor para.

Tradução da transformação de Fourier

Para tudo θ que pertence a um conjunto e T que pertence ao conjunto S ', você precisa:

τ_para F [θ] =  F [e^-IAX.θ]                                τ_para F [t ] =  F [e^-IAY . T]

Pode servir a você: Hypercubo: Definição, dimensões, coordenadas, desdobrado

Para tudo para que pertence a R

Transformação de Fourier de um grupo de escala

Para tudo θ que pertence a um conjunto S. T que pertence ao conjunto S '

λ pertencente a R - 0  se tem que:

F [θ (λx)] = (1 / | λ |) F [θ] (e/λ)                 

F [T (λx)] = (1 / | λ |) F [T] (e/λ)

Sim F É uma função contínua e puramente integrável, onde a> 0. Então:

F [f (at)] (z) =   (1/a) F [f (t)] (z/a) 

Para demonstrar esse resultado, podemos prosseguir com a mudança de variável.

Quando t → + então s = em → + ∞

Quando t → - então s = em → - ∞

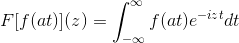
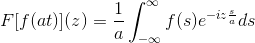
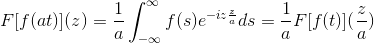
Simetria

Para estudar a simetria do Fourier Transform.

Você tem θ e δ que pertencem a S. A partir daí, pode -se deduzir que:

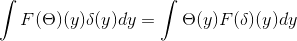
Obtenção

1 / (2π)^d  F [θ ], F [δ] Identidade parseval

1 / (2π)^D/2  || F [θ ] ||_eu²_R^d     Fórmula de Plancherel

Fourier se transformou de um produto em convolução

Perseguindo objetivos semelhantes que, no Laplace Transform, a convolução das funções refere -se ao produto entre suas transformações de Fourier.

Possui F e G como 2 funções limitadas, definidas e completamente integráveis:

F (f *g) = f (f) . F (g)

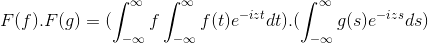
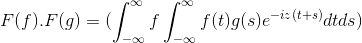
Então, ao fazer a mudança de variável

t + s = x; A dupla integral integral é continuada

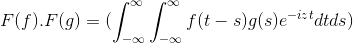
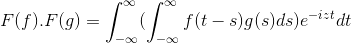
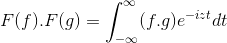
F (f) . F (g) = f (f . g)

Continuidade e cair no infinito

Para tudo θ que pertence a R, f [ θ] obedece aos critérios de função contínua limitada em r^d.

Também F [ θ] (y) → 0 em c si | y | → ∞

História

Este conceito matemático foi apresentado por Joseph B. Fourier em 1811 enquanto desenvolve um tratado sobre o Espalhe calor. Foi rapidamente adotado por vários ramos da ciência e engenharia.

Foi estabelecido como a principal ferramenta de trabalho no estudo de equações com derivados parciais, comparando mesmo com a relação de trabalho entre o Laplace transformou e equações diferenciais comuns.

Qual é a transformação de Fourier para?

Serve principalmente a equações significativas, enquanto transformando expressões derivadas em elementos de poder, que denotam expressões diferenciais na forma de polinômios integráveis.

Na otimização, modulação e modelagem de resultados, ele atua como uma expressão padronizada, sendo um recurso frequente para a engenharia após várias gerações.

Série de Fourier

Eles são séries definidas em termos de Cosen e seios; Eles servem para facilitar o trabalho com funções periódicas gerais. Quando aplicados, eles fazem parte das técnicas de resolução de equações diferenciais parciais e comuns.

Pode atendê -lo: função variável real e sua representação gráfica

As séries de Fourier são ainda mais gerais que a série de Taylor, porque desenvolvem funções periódicas de descontinua que não têm representação na série Taylor.

Outras formas da série Fourier

Para entender analiticamente a transformação de Fourier é importante.

-Série de Fourier em uma função do período 2L

Muitas vezes é necessário adaptar a estrutura de uma série de Fourier, a funções periódicas cujo período é p = 2l> 0 no intervalo [-l, l].

-Série de Fourier em funções pares e estranhas

O intervalo [-π, π] é considerado que oferece vantagens ao aproveitar as características simétricas das funções.

Se f é torque, a série Fourier é estabelecida como uma série de cosenos.

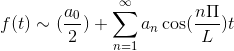
Se F é estranho, a série Fourier é estabelecida como uma série de seios.

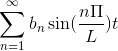
-Notação complexa da série Fourier

Se você tem uma função f (t), que atende a todos os requisitos desenvolvidos da série Fourier, é possível denotá-lo no intervalo [-t, t] usando sua notação complexa:

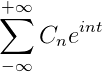
Formulários

Fonte: pexels

Cálculo da solução fundamental

A transformação de Fourier é uma ferramenta poderosa no estudo de equações diferenciais parciais do tipo linear com coeficientes constantes. Solicitar funções com domínios não limitados igualmente.

Como a transformação de Laplace, a transformação de Fourier transforma uma função de derivados parciais, em uma equação diferencial comum muito mais fácil de operar.

O problema de Cauchy para a equação de calor apresenta um campo frequente de aplicação da transformação de Fourier, onde a função é gerada Dirichlet Heat ou núcleo do núcleo.

Em relação ao cálculo da solução fundamental, são apresentados os seguintes casos onde é comum encontrar a transformação de Fourier:

-Equação de Laplace

-Equação de calor

-Equação de Schrödinger

-Equação de onda

Teoria do sinal

A razão geral para a aplicação da transformação de Fourier neste ramo se deve principalmente à decomposição característica de um sinal como uma sobreposição infinita de sinais mais facilmente tratáveis.

Pode ser uma onda sonora ou uma onda eletromagnética, a transformação de Fourier expressa em uma sobreposição simples de ondas. Esta representação é bastante frequente em engenharia elétrica.

Pode atendê -lo: linha vertical

Por outro lado, são exemplos de aplicação da transformação de Fourier no campo da teoria dos sinais:

-Problemas de identificação do sistema. Estabelecido f e g

-Problema com a consistência do sinal de saída

-Problemas com a filtragem de sinal

Exemplos

Exemplo 1

Defina a transformação de Fourier para a seguinte expressão:

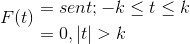
Também podemos representá -lo da seguinte forma:

F (t) = Sin (t) [h_{(T + K)} - H_{(T - K)} ]

O pulso retangular é definido:

p (t) = h_{(T + K)} - H_{(T - K)}

A transformação de Fourier é aplicada à próxima expressão que se assemelha ao teorema da modulação.

f (t) = p (t) sin (t)

Onde: F [w] = (1/2) I [P (W + 1) - P (W - 1)]

E a transformação de Fourier é definida por:

F [w] =  (1/2) i [(2/2W+1) Sen (K (W+1)) - (2/2W+1) Sen (K (W-1))]

Exemplo 2

Defina a transformação de Fourier para expressão:

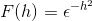Por definição, expressamos a transformação da seguinte maneira

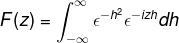
Como f (h) é uma função uniforme, pode -se afirmar que

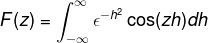Derivando na integral em relação a Z, a expressão pode ser reescrita. Esta etapa é significativa no trabalho com equações diferenciais.

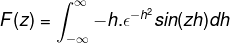
A integração por peças é aplicada selecionando as variáveis ​​e seus diferenciais da seguinte maneira

u = sin (zh) du = z cos (zh) dh

dv = h (e^-h)²                       V = (e^-h)² / 2

Substituindo -o

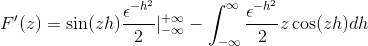
Depois de avaliar sob o teorema fundamental do cálculo

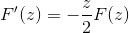
Aplicando conhecimentos anteriores relacionados às equações diferenciais da primeira ordem, a expressão é denotada como

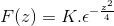
Para obter k, avaliamos 

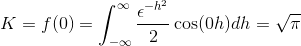
Finalmente, a transformação de Fourier é definida como

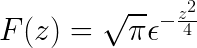
Exercícios propostos

• Determine a transformação da expressão de Fourier
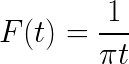
• Resolva a seguinte integral inadequada usando a igualdade de Pareseval
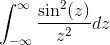
• Obtenha a transformação da expressão com (1+W²)

Referências

1. Duoandikoetxea zuazo, j., Análise de Fourier. Addison- Wesley Iberoamericana, Universidade Autônoma de Madri, 1995.
2. Lions, j. eu., Análise matemática e métodos numéricos para ciência e tecnologia. Springer-Verlag, 1990.
3. Lieb, e. H., Os grãos gaussianos têm apenas maximizadores gaussianos. Inventar. Matemática. 102, 179-208, 1990.
4. Dym, h., McKean, h. P., Série de Fourier e integrais. Academic Press, Nova York, 1972.
5. Schwartz, l., Théorie des Distribuições. Ed. Hermann, Paris, 1966.