Propriedades de transformações lineares, quais são o uso, tipos, exemplos

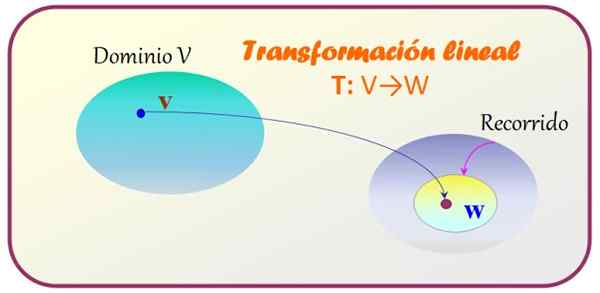
A Transformação linear, que simplesmente chamaremos, relaciona os elementos de dois espaços vetoriais V e W, atribuindo cada vetor v pertencente a V um único vetor C que pertence a W, através de uma operação específica.

Esta transformação atende a duas condições:

figura 1. Uma transformação linear se aplica a um vetor do Space V Vector para obter outro vetor pertencente ao espaço vetorial W. Fonte: f. Zapata.

-Condição 1

Refere -se à adição, de modo que uma transformação T -linear deve ser cumprida que:

T (v + C) = T (v) + T (C)

-Condição 2

A segunda condição representa homogeneidade na multiplicação de um escalar por um vetor:

T (cv) = C⋅t (v)

A transformação linear, como o nome indica, é responsável por mapear ou transformar elementos de V em elementos de W.

A notação para funções também é usada no caso de transformações lineares; portanto, o domínio de V é o conjunto de elementos (vetores) a serem transformados, enquanto o codomínio ou a rota é o conjunto resultante.

Um exemplo de transformação linear é:

Para indicar que a letra t será usada. A transformação será aplicada a um vetor v cujos componentes são x e y, que foi representado por uma única matriz de coluna. O resultado é outro vetor C cujos componentes são x e 0, também representados por uma matriz de coluna.

Portanto, esta é uma transformação do espaço vetorial r² Em direção ao espaço vetorial r², que em resumo está escrito assim:

T: r² → R²         

Se tivermos o vetor:

A transformação nos devolve:

E assim com qualquer vetor R². No Exemplo 1, será verificado que essa transformação é linear.

[TOC]

Propriedades de transformações lineares

Suponha uma transformação linear de V em W, em que os vetores v e ou Eles pertencem a V, então as seguintes propriedades são atendidas:

Propriedade 1

T (0) = 0

Onde 0 é o vetor nulo.

Propriedade 2

T (-v) = - t (v)

Propriedade 3

T (ou  - v) = T (ou) - T (v)

Propriedade 4

Ser v = c₁v₁ + c₂v₂ +.. . +  c_nv_n

 Então:

T (c₁v₁ + c₂v₂ +.. . +  c_nv_n) = c₁ T (v₁) + c₂ T (v₂) +.. . +  c_n T (v_n)

Elementos de transformação linear

Seja V e W já mencionaram espaços vetoriais onde a transformação linear t transforma elementos de V para W. Podemos definir os seguintes elementos:

-Núcleo c ou kernel: É um subconjunto do domínio para o qual é denotado por N (t) qualquer ker (t) e entender todos os elementos de V de tal forma que:

T (v) = 0.

A transformação linear t (v) = 0 se chama Transformação nula.

Naturalmente o vetor nulo v = 0 cumpre de qualquer maneira com essa condição, mas o kernel consiste em todo os vetores não -nula que também o cumprem, para um dado t.

Pode atendê -lo: função crescente: como identificá -lo, exemplos, exercícios

-Imagem de t: É o conjunto de vetores pertencentes a W, que são a imagem de pelo menos algum vetor em v. É denotado como EU SOU T) E é subconjunto do espaço vetorial w.

Esses elementos nos ajudarão a classificar transformações lineares mais tarde.

O que são transformações lineares para?

Inicialmente, as transformações lineares funcionam com espaços vetoriais, formados por vetores. Muitas vezes associamos vetores à força e outras magnitudes físicas, no entanto, no processamento de imagens digitais, um pixel pode ser representado por um vetor.

Nesse caso, a imagem pode ser manipulada por transformações lineares convenientes para obter os efeitos desejados, por exemplo, projetando, girando, encontrando a imagem do espelho ou modificando seu tamanho sem alterar as dimensões relativas.

Transformações lineares também são amplamente utilizadas em economia e tomada de decisão, por exemplo, para saber a quantidade de matéria -prima necessária para fabricar um determinado lote do produto.

O número de peças necessárias para montar os vários modelos produzidos por uma fábrica pode ser trabalhada através de um arranjo de matriz, como veremos mais adiante.

Tipos de transformações lineares (classificação)

Como funções, as transformações lineares podem ser:

-Injetivo ou monomorfismos

-Bijetivos ou Epimorfismos

-Superjetivo ou Isomorfismos

Além disso, são os seguintes tipos:

-Endomorfismos

-Automorfismos.

Transformações lineares injetivas

Deixe V e W espaços vetores e T uma transformação linear t: v → w. T é injetivo quando:

Ker (T) = 0

Transformações superjetivas lineares

Se V e W são os espaços vetoriais de modo que T: V → W, diz -se que T é bijetivo quando:

Im (t) = w

Transformações lineares bijjetivas

Uma transformação linear t: v → w é bijetiva quando é injetivo e superjetivo. Portanto, é cumprido que:

Ker (T) = 0 e Im (t) = w

Endomorfismos

São transformações lineares nas quais o domínio e o codomínio coincidem.

Automorfismos

Esse tipo de transformação linear são endomorfismos bijetivos.

Transformações lineares especiais

Operador linear

Uma transformação linear t: v → v, que vai de um espaço vetorial para o mesmo espaço vetorial é chamado Operador linear.

Transformação zero

Mencionado acima, a transformação zero é importante para encontrar o núcleo de uma transformação linear:

Pode servir você: tetradecágon

T: v → w tal que t (v) = 0 para qualquer v.

Transformação de identidade

T: v → v tal que t (v) = v  para qualquer v.

Transformação definida por uma matriz

T: v → w tal que t (v) = Av, onde A é uma matriz e v É um vetor de coluna.

Função linear

As funções lineares do tipo y = mx são transformações lineares. Tomemos, por exemplo, y = 3x e veja se atende às duas condições do início, testando com dois valores A e B: qualquer:

f (a+b) = 3 (a+b) = 3a+3b = f (a)+f (b)

f (ka) = 3 (ka) = k⋅ (3a) = k⋅f (a)

Na verdade é uma transformação linear.

Formulários

Transformações lineares têm aplicações matemáticas, como:

-Coordenar a rotação dos eixos.

-Na solução de sistemas de equações diferenciais lineares.

-Problemas de auto -valor e automóveis.

E eles também têm aplicações em outros campos da ciência, por exemplo, em mecânica, mecânica quântica e economia, entre outras áreas.

Exemplos de transformações lineares

Exemplo 1

Em muitos problemas mecânicos, precisamos encontrar a projeção de um vetor v pertencente ao espaço, em um certo avião. Este vetor v pode representar, por exemplo, uma força.

Suponha que você queira projetar o vetor v = No avião XY. Podemos definir uma transformação linear dada pela seguinte matriz:

Quando o aplicamos ao vetor v Temos um vetor cujo componente z é cancelado. Geometricamente é representado, com a projeção de v No avião XY como vetor vermelho com dois componentes.

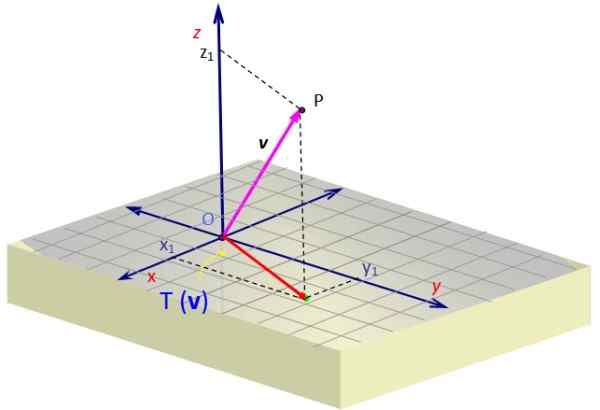Figura 2. Projeção de um vetor no espaço em um avião, que é obtido através de uma transformação linear. Fonte: f. Zapata.

Exemplo 2

Suponha que você tenha uma fábrica que produz três tipos de carrinhos de brinquedos: C1, C2 e C3, para os quais, por sua vez, precisa de três tipos de peças em certas quantidades para fabricar cada tipo de carrinho:

-Eixos ou peça

-Rodas ou peça b

-Chassi ou peça c

Para cada tipo de carrinho, o número de peças é diferente, pois os modelos são diferentes. Podemos acomodar as quantidades em uma matriz 3 × 3, na qual as colunas são chefiadas pelo tipo de carrinho, e as fileiras correspondem à quantidade de peças necessárias para elaborar cada modelo.

Este é um exemplo de transformação dada por uma matriz que seria assim:

Se a fábrica receber um determinado pedido de compra, que consiste em x quantidade de C1, e  de C2 e z De C3, quantas peças A, B e C precisam estar disponíveis para montar os carrinhos de pedidos?

Pode atendê -lo: o que são expressões algébricas e quais são as mais frequentes?

Precisamos encontrar uma transformação linear t (x) de modo que:

Para obter o vetor e:

Isso nos dará a quantidade de peças que devemos ter na disposição. No ano resolveu 2, avaliamos a eficácia das transformações lineares para encontrar a quantidade de peças necessárias para atender a uma determinada ordem.

Exercícios resolvidos

- Exercício 1

Verifique se a seguinte transformação t: r² → R² É linear:

Solução

Para fazer isso, você deve garantir que a transformação atenda às duas condições descritas no início, primeiro a adição e depois o produto de um escalar para um vetor. Então você tem que levar dois vetores v e  ou pertencente a r², Escrevendo -os por notação matricial ou especificando os componentes.

Esses vetores são:

v = x₁, e₁

ou = x₂, e₂

Primeira condição

-Lembrando que os vetores são adicionados componentes, deve -se verificar se:

T (v+ou) = T (v) + T (ou)

T (v+ou) = T (x₁+ x₂ ; e₁ + e₂)

Daqui é obtido que:

T (x₁+ x₂ ; e₁ + e₂) = (x₁+ x₂; 0)

-Por outro lado, ao aplicar a transformação a cada vetor separadamente:

T (x₁,e₁) + T (x₂,e₂) = (x₁,0) + (x₂,0)

Ao adicionar os vetores resultantes, é efetivamente obtido:

C = (X₁+ x₂; 0)

Como ambos os resultados são idênticos, a primeira condição é satisfeita.

Segunda condição

Agora vamos verificar se multiplicando por um escler c, ele pode sair da transformação:

T (cv) = C⋅t (v)

Sean:

v = x₁, e₁

c.v = C⋅x₁, C⋅y₁

Então:

T (cv) = T (C⋅x₁, C⋅y₁ ) = (C⋅x₁ , 0)

Mas sabemos que, a partir da etapa anterior, t (v) = T (x₁, e₁ ) = (X₁ , 0).

Assim, como ambas as expressões são idênticas, a segunda condição também é atendida e a transformação é linear.

- Exercício 2

Uma fábrica de carrinho de brinquedo reúne três modelos de veículos: C1, C2 e C3, para os quais você precisa de peças A, B e C, respectivamente, eixos, rodas e chassi. Os valores necessários estão na tabela a seguir:

A fábrica foi solicitada a preparar 12 modelos C1, 22 C2 e 16 C3. Quantas peças A, B e C são necessárias para concluir o pedido?

Solução

Transformação linear t (x) = y é aplicada, cujo resultado é o produto entre matrizes:

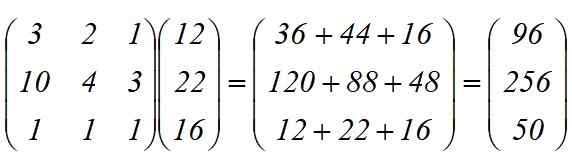
Eles são necessários no total:

-96 eixos

-256 rodas

-50 chassi.

Referências

1. Álgebra e geometria analítica. Núcleo e imagem. Classificação de transformações lineares. Recuperado de: aga.FRBA.Utn.Edu.ar.
2. Grossman, s. 2012. Álgebra Linear. 7º. Edição. McGraw Hill.
3. Gutiérrez, e. 2014. Álgebra linear e suas aplicações. Grupo editorial da Patria.
4. Larson, r. 2016. Fundamentos da álgebra linear. 6º. Edição. Cengage Learning.
5. Wikipedia. Aplicações lineares. Recuperado de: é.Wikipedia.org.