Trabalho mecânico O que é, condições, exemplos, exercícios

Ele Trabalho mecanico É definido como a mudança no estado energético de um sistema, causado pela ação de forças externas como gravidade ou atrito. As unidades de trabalho mecânico no sistema internacional (SI) são Newton X Metro ou Joules, abreviado por J.

Matematicamente, é definido como o produto escalar da força pela força pelo deslocamento vetorial. Sim F É a força constante e eu É o deslocamento, ambos os vetores, o trabalho w é expresso como: W = F ● eu

figura 1. Enquanto o atleta aumenta o peso, ele trabalha contra a gravidade, mas quando mantém o peso imóvel, do ponto de vista da física, ele não está trabalhando. Fonte: NeedPix.com

Quando a força não é constante, devemos analisar o trabalho realizado quando os deslocamentos são muito pequenos ou diferenciais. Nesse caso, se for considerado um ponto de partida a ponto A e como chegada a B, o trabalho total é obtido adicionando todas as contribuições para a mesma. Isso é equivalente a calcular a seguinte integral:

E, como afirmado no início, desde que haja uma mudança na energia do sistema, será porque existem forças do exterior agindo nela, portanto:

Variação na energia do sistema = trabalho realizado por forças externas

ΔE = W_ext

Quando a energia é adicionada ao sistema, w> 0 e quando é subtraído<0. Ahora bien, si ΔE = 0, puede significar que:

-O sistema está isolado e não há forças externas agindo nele.

-Existem forças externas, mas elas não estão trabalhando no sistema.

Como a variação de energia é equivalente ao trabalho realizado por forças externas, a unidade se a energia também for o joule. Isso inclui qualquer tipo de energia: cinético, potencial, térmico, químico e muito mais.

[TOC]

Condições para que haja trabalho mecânico

Já vimos que o trabalho é definido como um produto escalar. Vamos tomar a definição de trabalho realizado por força constante e aplicar o conceito de produto escalar entre dois vetores:

W = F ● L = F.eu.cos θ

Onde F É a magnitude da força, eu É a magnitude do deslocamento e θ É o ângulo que existe entre força e deslocamento. Na Figura 2, há um exemplo de força externa inclinada que atua em um bloco (o sistema), que produz um deslocamento horizontal.

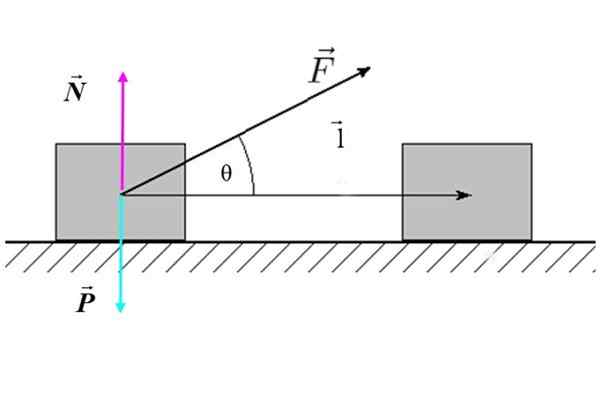Figura 2. Diagrama do corpo livre de um bloco que se move em uma superfície plana. Fonte: f. Zapata.

Reescrevendo o trabalho da seguinte forma:

W = (f. cos θ). eu

Podemos afirmar que apenas o componente da força é paralelo ao deslocamento: F. cos θ eé capaz de fazer trabalho. Se θ = 90º então cos θ = 0 e o trabalho seria anulado.

Portanto, conclui -se que as forças perpendiculares ao deslocamento não fazem trabalho mecânico.

No caso da Figura 2, nem a força normal N nem o peso P Eles funcionam, porque ambos são perpendiculares ao deslocamento eu.

Os sinais de trabalho

Como explicado acima, C Pode ser positivo ou negativo. Quando cos θ> 0, O trabalho realizado pela força é positivo, pois tem a mesma direção do movimento.

Pode servir a você: Número de massa: o que é e como obtê -lo (com exemplos)

Sim cos θ = 1, força e deslocamento são paralelos e o trabalho é máximo.

No caso de cos θ < 1, la fuerza no está a favor del movimiento y el trabajo es negativo.

Quando cos θ = -1, A força é completamente oposta ao deslocamento, como o atrito cinético, cujo efeito é parar o objeto em que age. Portanto, o trabalho é mínimo.

Isso concorda com o que foi dito no início: se o trabalho é positivo, a energia está sendo adicionada ao sistema e, se for negativo, está sendo subtraído.

Rede C_líquido É definido como a soma dos trabalhos realizados por todas as forças que atuam no sistema:

C_líquido = ∑W_Yo

Em seguida, podemos concluir que, para garantir a existência do trabalho mecânico líquido, é necessário que:

-As forças externas agem no objeto.

-Essas forças não são todas perpendiculares ao deslocamento (cos θ ≠ 0).

-Os trabalhos realizados por cada força não são cancelados.

-Há um deslocamento.

Exemplos de trabalho mecânico

-Sempre que for necessário colocar um objeto em movimento com base no descanso, é necessário fazer um trabalho mecânico. Por exemplo, empurre uma geladeira ou um tronco pesado em uma superfície horizontal.

-Outro exemplo de uma situação em que é necessário fazer um trabalho mecânico é mudar a velocidade de uma bola em movimento.

-É necessário trabalhar para levantar um objeto a uma certa altura no chão.

Agora, existem situações igualmente comuns em que Não o trabalho é feito, embora as aparências indiquem o contrário. Dissemos que, para levantar um objeto a uma certa altura, temos que trabalhar, então carregamos o objeto, elevamos -o acima da nossa cabeça e o mantemos lá. Estamos trabalhando?

Aparentemente sim, porque se o objeto estiver pesado, os braços se cansarão em breve, no entanto, não importa quanto trabalho seja feito, o trabalho não está sendo feito do ponto de vista da física. Porque não? Porque o objeto não está se movendo.

Outro caso em que, apesar de ter uma força externa, não realiza trabalho mecânico é quando a partícula tem um movimento circular uniforme.

Pode servir a você: esforço normal: o que consiste, como é calculado, exemplos

Por exemplo, uma criança que vira uma pedra amarrada a uma corda. A tensão da corda é a força centrípeta que permite a rotação da pedra. Mas sempre essa força é perpendicular ao deslocamento. Então não faça um trabalho mecânico, apesar do fato de favorecer o movimento.

O teorema da energia profissional Cinetics

A energia cinética do sistema é o que tem sob seu movimento. Sim m é a massa e v É a velocidade do movimento, a energia cinética é denotada por K E é dado por:

K = ½ mV²

Por definição, a energia cinética de um objeto não pode ser negativa, uma vez que a massa e o quadrado da velocidade são sempre quantidades positivas. A energia cinética pode ser 0, quando o objeto está em repouso.

Para mudar a energia cinética de um sistema, é necessário-. Para isso, é necessário fazer o trabalho líquido no sistema, portanto:

C_líquido = ΔK

Este é o teorema do trabalho - energia cinética. Afirma isso:

O trabalho líquido é equivalente à mudança na energia cinética do sistema

Observe que, embora K seja sempre positivo, ΔK pode ser positivo ou negativo, pois:

ΔK = k_final - K _inicial

Sim K_final >K _inicial O sistema ganhou energia e Δk> 0. Pelo contrário, sim K_final < K _inicial, O sistema produziu energia.

Trabalho feito para esticar uma primavera

Ao esticar (ou comprimir) uma mola, é necessário fazer um trabalho. Este trabalho é armazenado na primavera, permitindo que isso funcione, digamos, um bloco que é anexado a um de seus fins.

A lei de Hooke afirma que a força exercida por uma mola é uma força de restituição - é contrária ao deslocamento - e também proporcional ao referido deslocamento. A constante de proporcionalidade depende de como a primavera é: suave e facilmente deformável ou rígido.

Esta força é dada por:

F_r = -kx

Na expressão, F_r É a força, k É a primavera constante e x É o deslocamento. O sinal negativo indica que a força exercida pela mola se opõe ao deslocamento.

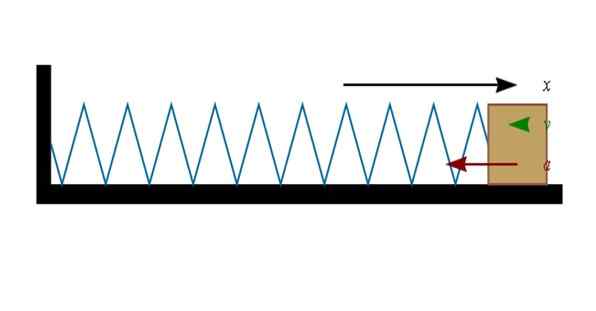Figura 3. Uma mola compactada ou esticada funciona em um objeto amarrado ao seu fim. Fonte: Wikimedia Commons.

Se a mola for comprimida (à esquerda na figura), o bloco no final se moverá para a direita. E quando a primavera for esticada (à direita), o bloco vai querer se mover para a esquerda.

Para comprimir ou esticar a mola, algum agente externo deve fazer o trabalho e, como é uma força variável, para calcular este trabalho, você deve usar a definição que ocorreu no início:

Pode atendê -lo: Darcy Law

É muito importante observar que este é o trabalho realizado pelo agente externo (a mão de uma pessoa, por exemplo) para comprimir ou esticar a mola. É por isso que o sinal negativo não aparece. E como as posições são quadradas, não importa se são compressões ou alongamentos.

O trabalho que fará a primavera, por sua vez, é:

C_primavera = -W_ext

Exercícios

Exercício 1

O bloco na Figura 4 tem massa m = 2 kg e desliza pelo plano inclinado sem atrito, com α = 36.9º. Supondo que seja permitido escorregar do restante do topo do avião, cuja altura é h = 3 m, encontre a velocidade com que o bloco atinge a base do plano, através do teorema da energia da energia cinética da energia.

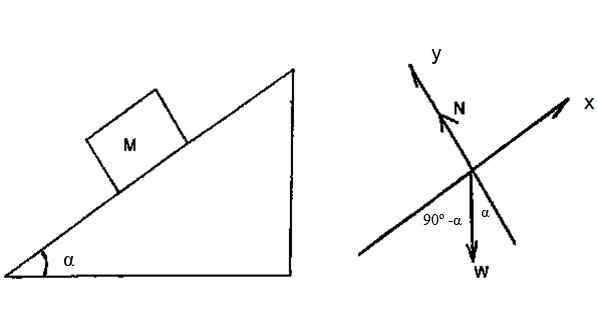Figura 4. Um bloco desliza para baixo em um avião inclinado sem esfregar. Fonte: f. Zapata.

Solução

O diagrama do corpo livre mostra que a única força capaz de trabalhar no bloco é o peso. Mais preciso: o componente de peso ao longo do eixo x.

A distância percorrida pelo bloco no avião é calculada por trigonometria:

D = 3 / (cos 36.9º) M = 3.75 m

C_peso = (Mg). d. cos (90-α) = 2 x 9.8 x 3.75 x cos 53.1º J = 44.1 j

Trabalhando o teorema da energia cinética:

C_líquido = ΔK

C_líquido = W_peso

ΔK = ½ mV_F²- ½ mv_qualquer²

Desde que é liberado do repouso, v_qualquer = 0, portanto:

C_líquido = ½ mv_F²

Exercício 2

Uma mola horizontal, cuja constante é k = 750 n/m é fixada por uma extremidade em uma parede. Uma pessoa comprime o outro final a uma distância de 5 cm. Calcule: a) a força exercida pela pessoa, b) o trabalho que ele fez para comprimir a mola.

Solução

a) A magnitude da força aplicada pela pessoa é:

F = kx = 750 n/ m . 5 x 10 ^-2 M = 37.5 n.

b) Se a extremidade da primavera estiver originalmente em x₁ = 0, para levar de lá para a posição final x₂ = 5 cm, é necessário fazer o seguinte trabalho, de acordo com o resultado obtido na seção anterior:

C_ext = ½ K (x₂² - x₁²) = 0.5 x 750 x (0.05² -0²) J = 0.9375 J.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dinâmico. Editado por Douglas Figueroa (USB).
2. IParraguirre, l. 2009. Mecânica básica. Coleção de ciências naturais e matemática. Distribuição online gratuita.
3. Cavaleiro, r. 2017. Física para cientistas e engenharia: uma abordagem de estratégia. Pearson.
4. Física Librettexts. Teorema da energia do trabalho. Recuperado de: Phys.Librettexts.org
5. Trabalho e energia. Recuperado de: física.Bu.Edu
6. Trabalho, energia e poder. Recuperado de: NCERT.Nic.em