Toroid ou Toro dona

Explicamos o que é um touro ou touro, suas características, volume, superfície, aplicações e mostramos vários exemplos

O que é um toroid?

Ele Toroid É um corpo geométrico tridimensional na forma de um arco, anel, anel, rosquinha ou rosquinha, daí o nome de "Toro Dona", pertencente à classe de objetos chamados chamados chamados Revolução sólidos.

Um toróide é gerado girando uma figura plana fechada, em torno de uma linha pertencente ao mesmo plano da figura, mas não a intercepta, como mostrado abaixo:

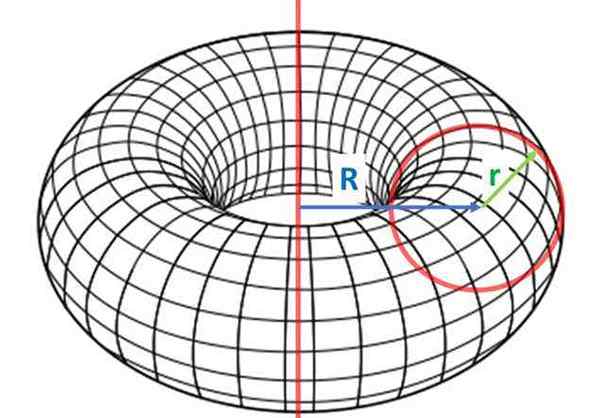
Um touro, que é uma superfície de revolução que é obtida girando uma figura plana fechada (como uma circunferência) em torno de um eixo fixo. Fonte: Wikimedia Commons

A principal característica do toróide é que, apesar de ser uma superfície fechada, tem um buraco. Isso significa que dois pontos de sua superfície podem ser conectados por um segmento que está fora do objeto.

Outra característica do toróide é que é uma figura tridimensional sem vértices. Essa característica o compartilha com outros corpos volumétricos, como a esfera, mas enquanto a esfera é uma superfície convexa, o touro é simultaneamente côncavo e convexo.

Entre os touros, o touro É o mais comum e é obtido a partir da rotação de um círculo de rádio r, Em relação a um eixo de distância R de primeira. A Radio R (em minúsculas) é conhecida como raio menor e r (capital) é o maior raio.

Volume de um toroid

Um touro é gerado girando uma figura plana fechada de área PARA em torno de um eixo de rotação que não o corta. Denotando por R A distância do eixo até o centróide da figura plana, o volume do touro da Revolução é:

Pode atendê -lo: funções trigonométricas inversas: valor, derivativos, exemplos, exercícios

V = 2πr⋅ A 

Este resultado é obtido ao aplicar o Teorema de Pappus Para o volume de um sólido de revolução, que afirma que o volume de qualquer revolução sólida é obtida multiplicando a área da figura que é quebrada pelo perímetro da circunferência formada pela rotação do centróide (ou centro de gravidade ) da figura girada, em torno do eixo de rotação.

Volume de um touro

O touro é o toroóide gerado por um círculo de rádio r. Se a distância do eixo de rotação até o centro do círculo girada for r, é necessário o volume de volume o touro é:

V = (2πr) ⋅ (πr²) = 2π²R³

Superfície de um touro

Ser uma figura plana simplesmente relacionada PARA e contorno eu. Se esse número for girado em torno de um eixo contido no mesmo plano da figura, mas isso não o atravessa, a superfície gerada é um touro de área:

S = 2πr⋅ L

Sendo a distância do eixo até o centro de gravidade ou centróide, da figura da Geratrix.

Este resultado é uma conseqüência de Teorema de Pappus Para a superfície de uma revolução sólida.

Superfície de um touro

O touro cruzado circular da Radio R (minúsculas) e o prefeito de rádio R (maiúsculos) é um touro em particular chamado Toro.

Como o contorno l de um círculo de raio r é 2πr, Então a área da superfície do referido touro é:

S = (2πr) ⋅ (2πr) = (4π²) (R⋅ r)

Aplicações de toroid

Devido às suas características geométricas, o touro tem inúmeras aplicações práticas e culturais. Para começar, aros ou anéis são peças toroidais que têm vários usos:

Pode atendê -lo: quadrados mínimos

Cultural

• Uso ornamental ou cosmético quando um anel é colocado em um dedo ou quando um piercing é colocado na orelha.
• No nariz do bois, é colocado um arco, o que serve para amarrá -lo e controlá -lo.
• Quando o anel ou anel é colocado na mão esquerda no dedo anelar, ele tem uma conotação social, que data da época dos gregos antigos, e denota compromisso, fidelidade e casamento com o casal que carrega um aro no mesmo maneira e material.

Em mecânica

Fora do contexto ornamental, cosmético e cultural, o touro tem muitas aplicações práticas. Na mecânica, o toróide é usado como um anel de retenção do rolamento na ponta do eixo do veículo. 

Além disso, os rolamentos dos veículos a motor são constituídos por um ou dois aros em uma forma de touro com várias formas de seção transversal, nas quais rolam cilindros ou esferas, com o objetivo de reduzir o atrito nos eixos.

Em eletricidade

Em aplicações elétricas, o toróide também é da maior importância, uma vez que os núcleos ferromagnéticos de indutores, eletromagadores e transformadores, geralmente têm uma forma de touro e neles um cabo na forma de bobina.

O tokamak

Existe um tipo de reator de fusão controlado na forma de um toróide ou rosquinha chamada por seu nome russo: TOkamak. Neste tipo de reator de fusão nuclear, o recipiente e as bobinas que produzem o campo magnético do confinamento de plasma têm uma forma ou disposição toroidal.

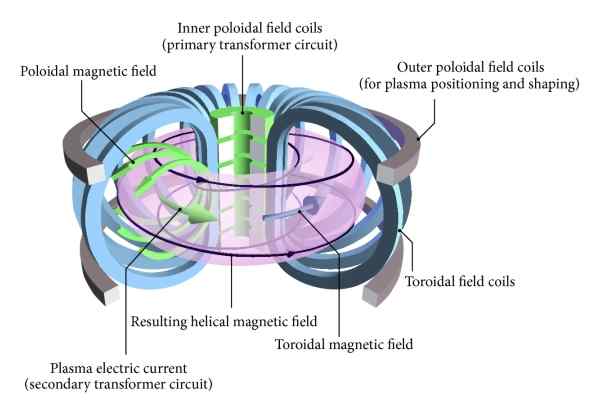A figura mostra esquematicamente um reator de fusão nuclear controlado em uma forma toroidal conhecida como "Tokamak". Nesse tipo de reator, o plasma, as bobinas e o campo magnético de confinamento têm uma configuração toroidal. Fonte: Wikimedia Commons

Exemplos

Superfície de um touro de seção quadrada (por fórmula)

Neste exemplo, um touro de seção quadrada é considerada como mostrado na figura a seguir:

Pode atendê -lo: Triângulo Scaleno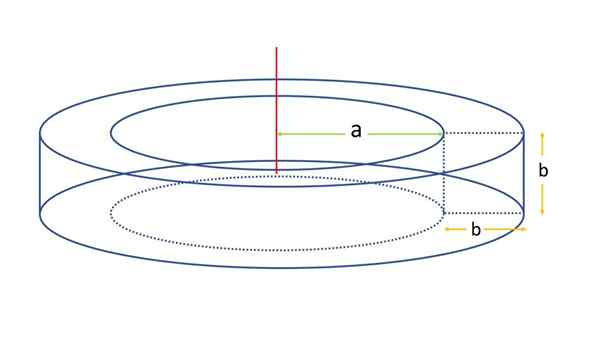 Seção quadrada toroid. Fonte: f. Zapata

A superfície será determinada usando a fórmula da superfície para um touro geral. Para esse fim, é necessário conhecer a distância do eixo de rotação ao centróide do quadrado, que, usando a nomenclatura anterior é R:

R = a + b/2

Também é necessário conhecer o perímetro eu da figura do Geratrix, que como neste caso é um quadrado no lado b, Seu contorno será longo:

L = 4⋅B

Então a fórmula da superfície de um touro é aplicada:

S = 2πr⋅l

Substituir R e L por suas expressões correspondentes, dependendo das medidas A e B do touro quadrado é:

S = 2π (a + b/2) ⋅4⋅b = 8π (a + b/2) ⋅b

Superfície quadrada toroóide (soma de seus rostos)

O touro quadrado da figura anterior é composto de quatro faces: o superior e o inferior são anéis planos, e o interior e o exterior são cilíndricos.

Levando isso em consideração, é possível calcular sua superfície adicionando a área de suas quatro faces.

As faces superior e inferior têm uma área igual à do círculo externo do raio (A+b) menos o do círculo interno do rádio para, que têm como resultado:

S_s= S_Yo= π [(a+b)² - b²] = π⋅ [a²+ 2AB]

A face cilíndrica interna tem uma área:

S₁= 2πab

E a face cilíndrica externa tem uma área:

S₂= 2π (a+b) b = 2πab+2πb²

Para que a área total do toróide seja a soma s_s+S_Yo+S₁+S₂:

A = 2π⋅ [a²+ 2AB]+2πab+2πab+2πb².