Recursos de tiro horizontal, fórmulas e equações, exercícios

Ele Tiro horizontal É o lançamento de um projétil com velocidade horizontal de uma certa altura e esquerda para a ação da gravidade. Sem levar em conta a resistência do ar, a trajetória descrita pelo celular terá a forma de um arco de parábola.

Projetar objetos horizontalmente é bastante comum. Os projéteis são jogados com todos os tipos de pontas: das pedras com as quais as barragens foram desanimadas no início da história, até aquelas que são realizadas em esportes de bola e são seguidos de perto por multidões.

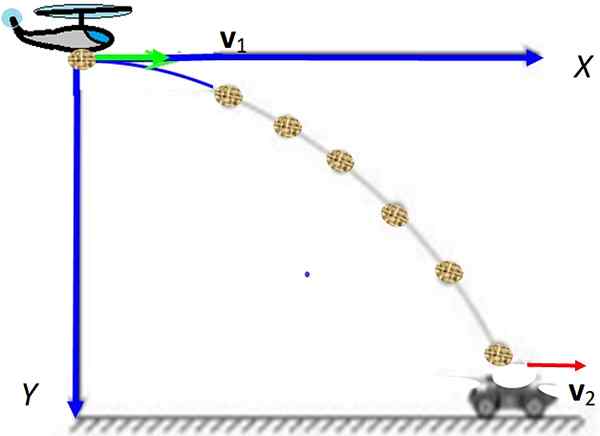
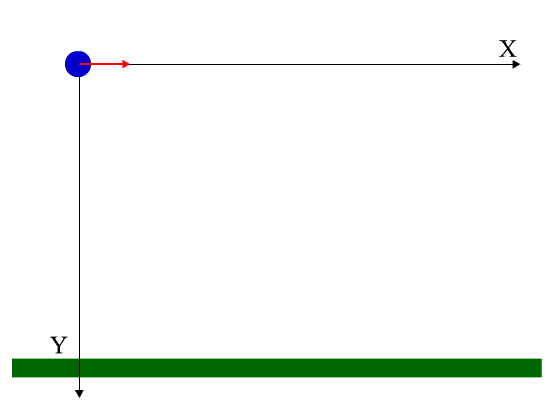figura 1. Tiro horizontal com componentes de velocidade vermelha. Observe que o componente horizontal permanece constante enquanto a vertical cresce. Fonte: Wikimedia Commons.

[TOC]

Caracteristicas

As principais características do tiro horizontal são:

-A velocidade inicial fornecida ao projétil é perpendicular à gravidade.

-O movimento ocorre em um avião, então são necessárias duas coordenadas: x e e.

-Isso é feito a partir de uma certa altura h acima do nível do solo.

-O tempo que o projétil dura no ar é chamado hora do voo.

-Fatores como resistência ao ar ou flutuações não são levados em consideração no valor de g.

-A forma, tamanho e massa do projétil não influenciam seu movimento.

-O movimento se decompõe em dois movimentos simultâneos: um vertical abaixo da ação de g; O outro, horizontal, com velocidade constante.

Fórmulas e equações

As equações cinematográficas para o lançamento horizontal são obtidas das equações de queda livre e as do movimento retilíneo uniforme.

Pode atendê -lo: energia interna

Como a animação mostra claramente na Figura 1, o projétil é fornecido com uma velocidade inicial horizontal, indicada como v_qualquer = v_boi Yo (O texto em negrito de impressão indica que é um vetor).

Note -se que a velocidade inicial tem magnitude v_boi e é direcionado ao longo do eixo x, Qual é a direção do vetor da unidade Yo. Na animação, também é avisado de que a velocidade inicial não tem componente vertical, mas quando cai, esse componente está aumentando uniformemente, graças à ação de g, aceleração da gravidade.

Quanto ao componente horizontal da velocidade, ele permanece constante enquanto o movimento dura.

De acordo com o que foi dito, as posições são estabelecidas em função do tempo, tanto no eixo horizontal quanto no eixo vertical. A direita é tomada como +x eixo, enquanto abaixo é o endereço -e. O valor da gravidade é G = -9.8 m/s² qualquer -32 pés/s²:

x (t) = x_qualquer + v_boi.t (posição horizontal); v_boi é constante

e (t) = y_qualquer + v_Oy.T - ½ g.t² (posição vertical); v_e = v_Oy - g.T (velocidade vertical)

Posição, velocidade, tempo de voo e faixa horizontal máxima

As equações são simplificadas se escolherem as seguintes posições iniciais: x_qualquer = 0, e_qualquer = 0 no local de lançamento. Além do mais v_Oy = 0, Como o celular é projetado horizontalmente. Com esta escolha, as equações de movimento são assim:

x (t) = V_boi.t; v_x = v_boi

e (t) = - ½ g.t²; v_e = - g.t

Quando o tempo não estiver disponível, a equação que relaciona velocidades e deslocamentos é útil. Isso é válido para a velocidade vertical, uma vez que a horizontal permanece constante ao longo do movimento:

Pode servir a você: Fluoreto de cálcio (CAF2): estrutura, propriedades, usos

v_e² = v_Oy² + 2.g .y = 2.g.e

Hora do voo

Para calcular o Tempo de voo t_voo, Suponha que o celular seja projetado a partir de uma altura H sobre o chão. Como a origem do sistema de referência no ponto de lançamento foi escolhida, quando atinge o terreno, está em posição -H. Substituindo isso na Equação 2) é obtido:

-H = - ½ g.t²_voo

t_voo = (2h/g)^½

Faixa máxima

Ele Alcance horizontal Este tempo é obtido substituindo x (t):

x_Máx = v_boi. (2h/g)^½

Exercícios resolvidos

-Exercício resolvido 1

Um helicóptero voa horizontalmente, mantendo uma elevação constante de 580 m quando libera uma caixa que contém alimentos em um campo de refugiados. A caixa cai a uma distância horizontal de 150 m do ponto de seu lançamento. Encontre: a) o tempo de voo da caixa.

b) a rapidez do helicóptero.

c) A rapidez com que a caixa tocou?

Solução

a) A altura h a partir da qual a comida é liberada é H = 500 m. Com esses dados ao substituir, você recebe:

t_voo = (2h/g)^½= (2 x 580/9.8) ^½S = 10.9 s

b) O helicóptero carrega a velocidade inicial horizontal v_boi do pacote e como um dos dados é x_máx:

x_Máx = v_boi. (2h/g)^½ ® v_boi = x_Máx /(2h/g)^½= x_Máx / t_voo = 150 m/ 10.9 s = 13.8 m/s

c) A velocidade do projétil a qualquer momento é:

v_e = -g.T = -9.8 m/ s² x 10.9 s = -106.82 m/s = - 384.6 km/h

O sinal negativo indica que o celular se move para baixo.

-Exercício resolvido 2

De um avião que voa horizontalmente a uma altura H = 500 m e 200 km/h Um pacote cai que deve cair em um veículo aberto que marcha para 18 km/h na estrada. Em que posição o avião deve deixar o pacote cair no veículo? Não leve em consideração a resistência do ar ou a velocidade do vento.

Pode atendê -lo: análise dimensionalFigura 2. Esquema para o exercício resolvido 2. Fonte: preparado por f. Zapata.

Solução

É conveniente passar primeiro todas as unidades para o sistema internacional:

18 km/h = 6 m/s

200 km /h = 55 m /s

Existem dois celulares: plano (1) e veículo (2) e é necessário escolher um sistema de coordenadas para localizar os dois. É conveniente fazê -lo no ponto de partida do pacote no avião. O pacote é projetado horizontalmente com a velocidade que o avião carrega: v₁, Enquanto o veículo se move para v₂ suposto constante.

-Avião

Posição inicial: x = 0; y = 0

Velocidade inicial = v₁ (horizontal)

Equações de posição: e (t) = -½g.t²  ; x (t) = V₁.t

-Veículo

Posição inicial: x = 0, y = -h

Velocidade inicial = v₂  (constante)

x (t) = x_qualquer + v₂. t

O tempo em que o voo do pacote dura é:

t_voo = (2h/g)^½ = (2 × 500/9.8)^½S = 10.1 s

Neste momento, o pacote experimentou um deslocamento horizontal de:

x_Máx = v_boi . (2h/g)^½= 55 m/s x 10.1 s = 556 m.

Neste momento, o veículo também se moveu horizontalmente:

x (t) = V₁.T = 6 m/s x10.1 s = 60.6 m

Se o avião lançar o pacote imediatamente que o veículo vê o trânsito sob ele, não será capaz de cair diretamente nele. Para que isso aconteça, ele deve jogá -lo de volta:

D = 556 m - 60.6 m = 495.4 m.

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 74-84.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).117 - 164.
3. Movimento do projétil. Recuperado de: Phys.Librettexts.org.
4. Rex, a. 2011. Fundamentos da Física. Pearson. 53-58.
5. Tiptens, p. 2011. Física: conceitos e aplicações. 7ª edição. McGraw Hill. 126-131.