Tipos de ângulos, características e exemplos

Existem diversos Tipos de ângulos, Levando em consideração vários critérios para diferenciá -los, por exemplo, eles podem ser distinguidos através de sua medida, pela posição que ocupam e também de acordo com a soma com outros ângulos.

Geralmente um ângulo é definido como a abertura entre dois semi -reta com uma origem comum, chamada de vértice do ângulo. O amplitude A abertura é a medida do ângulo, que freqüentemente vem em graus ou radianos.

Um grau é equivalente a uma das 360 partes em que uma circunferência pode ser dividida. Se a circunferência for dividida em duas partes iguais, cada uma é igual a 180 graus ou 180º, se for dividida em quatro partes iguais, cada um será de 90º e assim por diante. Este sistema é chamado Sexagesimal.

Radianes é outra medida muito usada, que consiste em tomar uma circunferência e medir o ângulo entre dois de seus rádios, cujo comprimento é "r" e com o vértice no centro da circunferência. Dessa maneira, o arco "s" entre esses rádios é afirmado "r" também e o ângulo subtendido é 1 radián ou 1 rad e é igual a 57.3º graus.

O instrumento para medir ângulos é o transportador. Para fazer uma medida, o centro do transportador é coincidido com o vértice do ângulo e um dos lados do mesmo com a linha 0º do transportador. O outro lado coincide com a medida do ângulo, que é lido na escala.

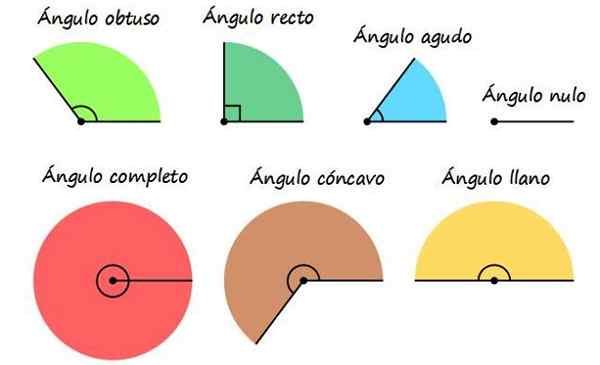
Tipos de ângulos de acordo com sua medida

Classificação de ângulos por sua medida. Fonte: Wikimedia Commons.

Uma das maneiras mais frequentes de se referir a ângulos é nomeá -los de acordo com sua medida, embora às vezes um ângulo possa pertencer a mais de uma categoria de descrito abaixo.

Pode servir a você: coeficiente de variação: para que serve, cálculo, exemplos, exercícios

Ângulo nulo

Aquele cuja medida é 0º ou 0 rad, ou seja, os dois semi -reta têm uma abertura zero.

Ângulo agudo

A medida de um ângulo agudo está entre 0 e 90º ou entre 0 e π/2 radianos. Por exemplo, ângulos de 30º, 45º e 60º, que fazem parte dos ângulos notáveis, são todos ângulos agudos.

Ângulo reto

É o que mede exatamente 90º (π/2 radianos), isso significa que os semi -textos que o definem são perpendiculares um ao outro.  Os ângulos internos de um quadrado ou um retângulo são ângulos retos e também é um ângulo reto que é formado entre os catetes de um triângulo retângulo.

Ângulo obtuso

É um ângulo maior que 90º ou π/2 radianos.

Ângulo plano

Mede exatamente 180º, equivalente a π radianes. Quando uma magnitude vetorial é oposta a outra, eles formam um ângulo de 180º, por exemplo, a velocidade de um celular que se move em uma linha reta e a desaceleração experimentada quando está sendo interrompida.

Ângulo convexo

Sempre que um ângulo mede menos de 180º é um ângulo convexo. Um ângulo agudo pode ser convexo, como um dos 90º e os ângulos obtusos cuja medida está incluída em 90º e 180º. Mais exemplos de ângulos convexos são:

• 45º
• 60º
• 75º
• 135º

Ângulo côncavo

É o que mede mais de 180º, como 225º ou 270º, o último é igual a três trimestres da circunferência.

Ângulo completo ou perigonal

Sua medida é 360º ou 2π radianos. Isso significa que os dois semi -textos que a compõem coincidem novamente, mas, diferentemente do ângulo nulo, neste caso houve uma curva completa.

Pode servir a você: oval (figura geométrica): características, exemplos, exercícios

Tipos de ângulos de acordo com a posição de seus lados

Em muitas figuras e estruturas geométricas, mais de um ângulo aparece e é por isso que é conveniente ter um critério para comparar os lados de um em relação a outro. Dessa forma, eles têm:

Ângulos consecutivos

Os ângulos consecutivos estão próximos um do outro, portanto eles têm um lado comum e vértice.

Ângulos adjacentes

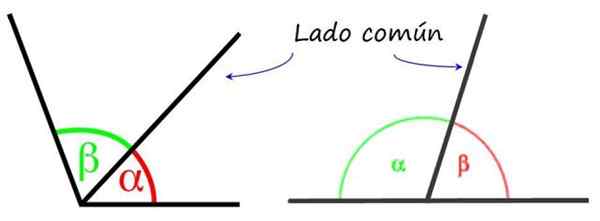À esquerda, dois ângulos consecutivos e nos dois ângulos adjacentes à direita. Fonte: Wikimedia Commons/F. Zapata.

Os ângulos adjacentes têm um lado comum e vértice, ou seja, eles se apresentam ao lado do outro. Mas, diferentemente dos ângulos consecutivos, nos ângulos adjacentes, os lados restantes são opostos semi -rastreados, portanto, entre os dois ângulos, total 180º.

Ângulos opostos pelo vértice

Os ângulos opostos do vértice têm o vértice em comum, e seus lados se estendem opostos, de um dos ângulos para o outro. Dessa forma, os ângulos opostos do vértice têm a mesma medida.

A figura a seguir mostra 4 ângulos, indicados com cartas gregas. Os ângulos azuis são α e β e, como pode ser visto, eles são ângulos agudos e opostos pelo vértice. Por outro lado, os ângulos γ e δ são ângulos obtusos e também são opostos pelo vértice.

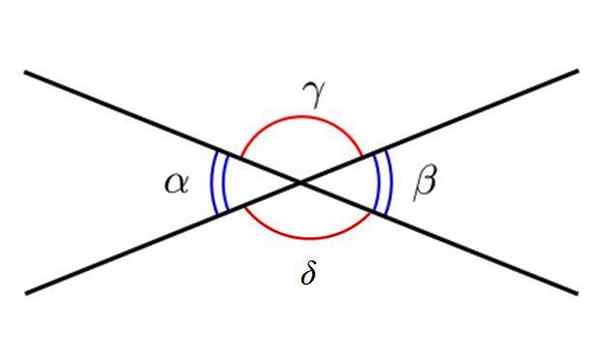Ângulos opostos pelo vértice. Fonte: Wikimedia Commons.

Tipos de ângulos de acordo com a soma de suas medidas

Alguns cálculos, especialmente na trigonometria, são muito simplificados ao observar se a soma das medidas de dois ângulos é a de um dos ângulos notáveis, como o ângulo reto (90º) ou o ângulo plano (180º). De acordo com isso, eles têm:

Ângulos complementares

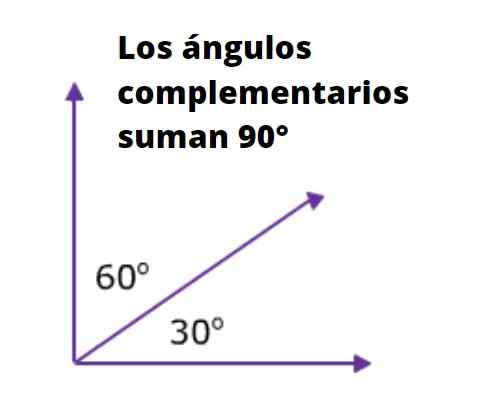
Aqueles ângulos cuja soma é igual a 90º são complementares. Por exemplo, os ângulos agudos internos de um triângulo retângulo são complementares, uma vez que a soma de seus três ângulos internos é igual a 180º.

Pode atendê -lo: 90 divisores: o que são e explicação

Como um dos ângulos internos do triângulo retângulo mede 90º, a soma dos outros dois também é igual a 90º.

Ângulos suplementares

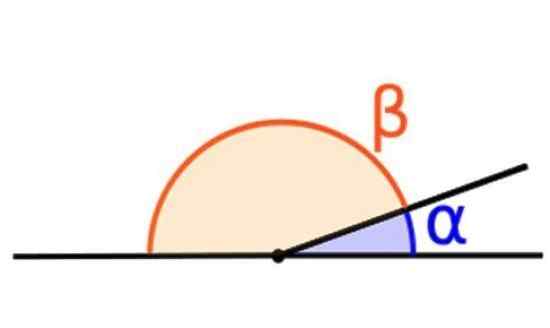A soma de dois ângulos suplementares é igual a 180º. Fonte: Wikimedia Commons.

São aqueles ângulos cuja soma é igual a 180º. Por exemplo, os ângulos α e β mostrados na figura superior.

Exemplos de ângulos notáveis ​​que são ao mesmo tempo suplementares são:

• 120º e 60º
• 135º e 45º

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Baldor. 1983. Geometria plana e espacial e trigonometria. Grupo de pátria cultural.
3. E. PARA. 2003. Elementos de geometria: com exercícios e geometria da bússola. Universidade de Medellin.
4. Geometria 1ª. Ângulos na circunferência. Recuperado de: edu.Xunta.é.
5. Rich, b. Geometria. 1991. Série Schaum. 2º. Edição. McGraw Hill.