Terceira Lei de Fórmulas, Equações, Exemplos de Termodinâmica

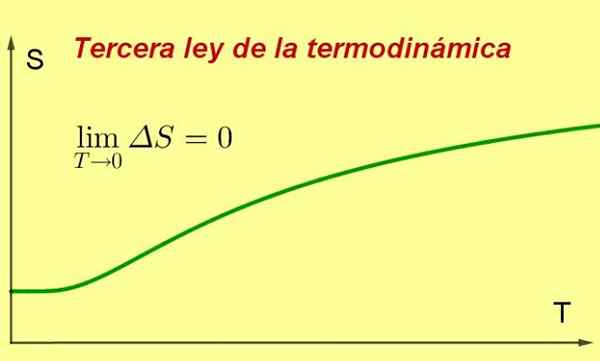
O Terceira Lei da Termodinâmica afirma que a entropia de um sistema termodinâmico fechado em equilíbrio tende a ser mínimo e constante, à medida que sua temperatura se aproxima de 0 Kelvin.

Este valor da entropia será independente das variáveis ​​do sistema (a pressão ou o campo magnético aplicado, entre outros). O que acontece é que, à medida que a temperatura está mais próxima de 0 K, os processos no sistema são interrompidos e como a entropia é uma medida de agitação interna, necessariamente desce.

figura 1. À medida que a temperatura de um sistema se aproxima do zero absoluto, sua entropia atinge um valor mínimo e constante. Fonte: preparado por f. Zapata ..

[TOC]

Conceitos anteriores

Para entender o escopo da terceira lei da termodinâmica, relevante para temperaturas muito baixas, é necessário revisar os seguintes conceitos:

Sistema termodinâmico

Geralmente se refere a um gás, um líquido ou um sólido. O que não faz parte do sistema é chamado em volta. O sistema termodinâmico mais comum é o gás ideal, que consiste em N partículas (átomos) que apenas interagem através de colisões elásticas.

Sistemas isolados, fechados ou abertos

Sistemas isolados não têm nenhuma troca com o ambiente. Sistemas fechados não trocam matéria com o meio ambiente, mas calor. Finalmente, os sistemas abertos podem trocar matéria e calor com o meio ambiente.

Macro -Estado e Microstate

O estado macro de um sistema é o conjunto de valores que têm suas variáveis: pressão, temperatura, volume, número de toupeiras, entropia e energia interna. Por outro. 

Muitos microestados podem resultar no mesmo estado macro. Em um gás à temperatura ambiente, o número de possíveis microestados é imenso, porque o número de partículas que o compõem, as diferentes posições e as diferentes energias que eles podem adotar é muito grande. 

Fórmulas e equações

Entropia como dissemos, é uma variável macroscópica termodinâmica que mede o sistema de transtorno molecular do sistema. O grau de desordem de um sistema é maior na medida em que o número de microestados possíveis é maior. 

Este conceito é necessário para formular a terceira lei da termodinâmica em forma matemática. Seja a entropia do sistema, então:

Isso significa que a entropia s em um sistema fechado não muda quando sua temperatura t tende a zero absoluto.

A entropia é uma variável de estado macroscópico que está diretamente relacionado ao número de possíveis microestados de um sistema, por meio da seguinte fórmula:

S = k ln (w)

Na equação anterior: S representa entropia, C o número de microestados possíveis do sistema e k É constante de Boltzmann (K = 1.38 x 10^-23 J/k). Isto é, a entropia de um sistema é k vezes o logaritmo natural do número de microestados possíveis.

Cálculo da entropia absoluta de uma substância

É possível definir a entropia absoluta de uma substância pura com base na definição da variação da entropia:

Onde Δq é a variação infinitesimal de calor e t é a temperatura. Esta equação é válida se o processo for reversível (Rev).Se for um processo isobárico - de pressão constante, o calor trocado durante uma variação de temperatura infinitesimal pode ser escrito assim:

ΔQ = n . c_p .Dt

Aqui CP é o calor molar específico e o número de toupeiras. A dependência de calor específica do molar com a temperatura é um fato obtido experimentalmente e conhecido por muitas substâncias puras.

Pode servir a você: Sistema Solar: Planetas, Características, Origem, Evolução

De acordo com a terceira lei em substâncias puras: 

Então o entropia absoluta de um mol de substância pura, como:

Na notação anterior, a barra indica que é a entropia de uma mol de substância e o Superson º denota uma substância pura.

Formulários

Na vida cotidiana, a terceira lei da termodinâmica tem poucas aplicações, bastante contrárias à primeira e segunda lei. É porque é um princípio que se refere ao que acontece em um sistema quando se aproxima do absoluto 0, um posto de temperatura rara.

De fato, alcance o absoluto ou -273,15 ° C é impossível (veja o exemplo 1 mais tarde), no entanto, a terceira lei é aplicada ao estudar a resposta dos materiais a temperaturas muito baixas. 

Graças a isso, surgiram avanços importantes no assunto condensado, como:

-Superfluidade (veja o exemplo 2 mais tarde)

-Supercondutividade 

-Técnicas de resfriamento a laser 

-Condensado de Bose-Einstein 

-Gases supérfluos de Fermi.

Figura 2. Hélio líquido supérfluo. Fonte: Wikimedia Commons.

A temperaturas extremamente baixas, a descida da entropia permite o surgimento de fenômenos quânticos interessantes. Portanto, vamos ver o que acontece com a entropia de um sistema de temperatura muito baixa.

Entropia de um sistema de baixa temperatura

Quando você tem uma substância cristalina perfeita, sua entropia mínima é exatamente zero, pois é um altamente arrumado. Em temperaturas próximas ao absoluto 0, a matéria está em estado condensado (líquido ou sólido) e as vibrações de vidro são mínimas.

Alguns autores consideram uma declaração alternativa da terceira lei da termodinâmica, o seguinte:

"Se a matéria condensa formando um cristal perfeito, quando a temperatura tende a zero absoluto, a entropia tende exatamente a zero". 

Vamos pontuar alguns aspectos da declaração anterior: 

- Um cristal perfeito é aquele em que cada molécula é idêntica e na qual a estrutura molecular é repetida de forma idêntica na sua totalidade.

- À medida que a temperatura tende a zero absoluto, a vibração atômica diminui quase completamente.

Então o vidro forma uma única configuração ou micro -estateração possível, ou seja, W = 1, E, portanto, a entropia é igual a zero:

 S = k ln (1) = 0

Mas não enquanto um material resfriado perto do zero absoluto forma um cristal, muito menos esse cristal é perfeito. Isso ocorre apenas se o processo de resfriamento for muito lento e reversível.

Caso contrário, fatores como impurezas presentes no vidro possibilitariam a existência de outros microestados. Portanto, w> 1 e entropia seriam maiores que 0.

Entropia residual

Se o processo de resfriamento for abrupto, durante o mesmo o sistema passa por uma sucessão de estados de não equilíbrio, o que leva ao material a mostrar. Nesse caso, não há estrutura cristalina e ordenada, mas um sólido amorfo, cuja estrutura é semelhante à de um líquido. 

Nesse caso, o valor mínimo de entropia nas proximidades de zero absoluto não é zero, uma vez que o número de microestados é muito maior que 1. A diferença entre essa entropia e a entropia nula do estado cristalino perfeito é conhecido como o entropia residual.

A explicação é que, abaixo de uma certa temperatura limite, o sistema não tem outra possibilidade senão ocupar.

Pode servir a você: Primeira Lei da Termodinâmica: Fórmulas, Equações, Exemplos

Eles serão responsáveis ​​por manter a entropia constante, mesmo que a temperatura continue a descer em direção a zero absoluto.

Exemplos

Exemplo 1: o zero absoluto e a indeterminação de Heisenberg

O princípio da indeterminação de Heisenberg estabelece que a incerteza na posição e o momento de uma partícula, por exemplo, nos átomos de uma rede cristalina, não são independentes do outro, mas seguem a seguinte desigualdade:

Δx ⋅ Δp ≥ h

Onde h é constante de Planck. Ou seja, a incerteza na posição multiplicada pela incerteza no momento (massa por velocidade) é maior ou igual à constante de Planck, cujo valor é muito pequeno, mas não zero: H = 6.63 x 10-3. 4 J · s.

E o que o princípio da incerteza tem a ver com a terceira lei da termodinâmica? Se a posição dos átomos da rede cristalina for fixa e precisa (Δx = 0) Então a velocidade desses átomos pode assumir qualquer valor entre 0 e o infinito. Isso é contradito pelo fato de que, em absoluto zero, todo movimento de agitação térmica cessa.

Reciprocamente, se iniciarmos isso em absoluto zero de temperatura, toda a agitação cessa e o momento de cada átomo da rede é exatamente zero (ΔP = 0), então o princípio da incerteza de Heisenberg implicaria que a indeterminação nas posições de cada átomo seria infinita, ou seja, eles podem estar em qualquer posição. 

Como conseqüência da declaração anterior, o número de microestados tenderia a infinito e a entropia também levaria valor indeterminado. 

Exemplo 2: Superfluidade e o estranho caso de hélio-4

Na supérflua, que ocorre em temperaturas muito baixas, a matéria perde o atrito interno entre suas moléculas, chamadas gosma. Nesse caso, o fluido pode circular sem atrito para sempre, mas o problema está naquelas temperaturas quase nada é líquido, exceto o hélio.

O helium e o hélio 4 (seu isótopo mais abundante) constituem um caso único, pois na pressão atmosférica e a temperaturas próximas ao zero absoluto, o hélio permanece líquido. 

Quando o hélio-4 é enviado a uma temperatura abaixo de 2.2 K à pressão atmosférica se torna um supérfluo. Essa descoberta ocorreu em 1911 em Leyden pelo físico holandês Heike Kamerlingh Onnes (1853-1926).

Figura 3. Físico holandês Heike Kamerlingh Onnes (1853-1926). Fonte: Wikimedia Commons.

Helio-4 Atom é um Bosón. Bósons, ao contrário de férmions, são partículas que podem ocupar o mesmo estado quântico. Portanto, os bósons não atendem ao princípio de exclusão de Pauli.

Então todos os átomos de hélio-4 a temperaturas abaixo de 2.2 K Ocupy o mesmo estado quântico e, portanto, não há nada mais do que um único microstato possível, o que implica que o hélio supérfluo-4 tem s = 0.

Exercícios resolvidos

- Exercício 1

Considere um caso simples que consiste em um sistema formado apenas por três partículas que possuem três níveis de energia. Para este sistema simples:

a) Determine o número de microestados possíveis para três faixas de temperatura:

-alto 

-Metade 

-Baixo

b) Determine através da entropia da equação de Boltzmann nos diferentes intervalos de temperatura. 

c) Discuta os resultados e explique se deve ou não contradizer a terceira lei da termodinâmica.

Solução para

Em uma escala molecular e atômica, as energias que um sistema pode adotar são quantizadas, o que significa que apenas certos valores discretos podem tomar. Além disso, quando as temperaturas são tão baixas, as partículas que compõem o sistema só têm a possibilidade de ocupar menos níveis de energia. 

Pode servir a você: Indução magnética: fórmulas, como é calculado e exemplos

Alta temperatura

Se o sistema tiver uma temperatura relativamente alta, as partículas terão energia suficiente para ocupar os níveis disponíveis, dando origem a 10 microestados possíveis, que aparecem na figura a seguir:

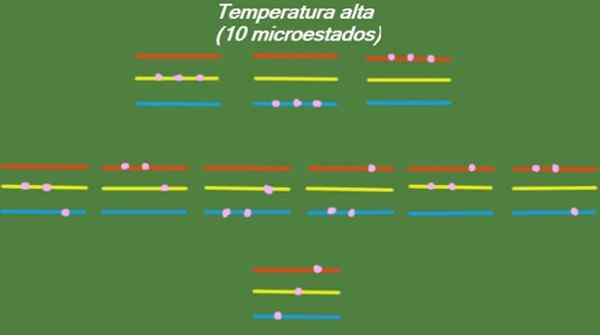Figura 4. Possíveis estados em alta temperatura para o ano resolvido 1. Fonte: preparado por f. Zapata.

Temperatura média

No caso de o sistema possuir uma temperatura intermediária, as partículas que o inventam não têm energia suficiente para ocupar o nível mais alto de energia. Os possíveis microestados são ilustrados na figura:

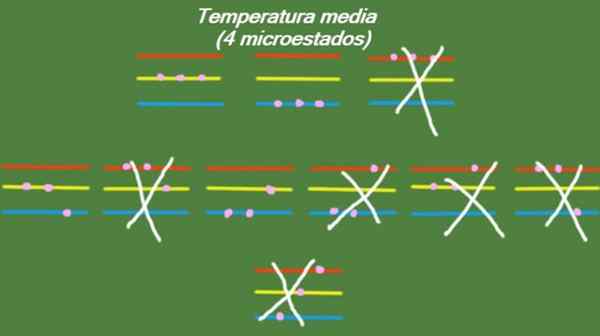Figura 5. Micro -Estado a temperatura média para o sistema de exercícios resolvido 1. Fonte: preparado por f. Zapata.

Temperatura baixa

Se a temperatura continuar descendo em nossas três partículas idealizadas e três níveis de energia, as partículas terão tão pouca energia que só poderão ocupar o nível mais baixo. Nesse caso, há apenas 1 microstato possível, como pode ser visto na Figura 6:

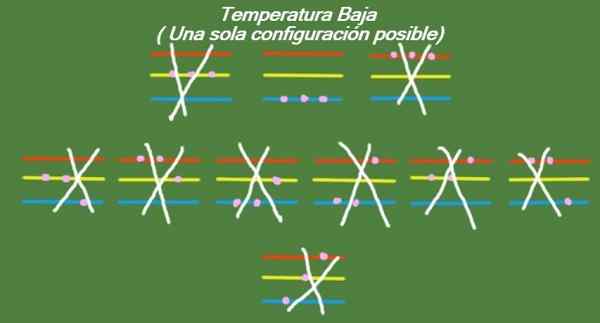Figura 6. A baixa temperatura, existe uma configuração possível (elaboração própria)

Solução b

Já conhecido o número de microestados em cada faixa de temperatura, já podemos usar a equação de Boltzmann dada anteriormente para encontrar entropia em cada caso.

S = k ln (10) = 2.30 x k = 3.18 x 10-23 J/k (Alta temperatura)

S = k ln (4) = 1.38 x k = 1.92 x 10-23 J/k (Temperatura média)

E finalmente:

S = k ln (1) = 0 (Temperatura baixa)

Solução c

Em primeiro lugar, notamos que a entropia diminui à medida que a temperatura desce, como esperado. Mas para os valores mais baixos de temperatura, é atingido um valor limite, a partir do qual o status base do sistema é alcançado.

Mesmo que a temperatura esteja o mais próxima possível de zero absoluto, não há estados menores disponíveis. Em seguida, a entropia mantém seu valor mínimo constante, que em nosso exemplo é s = 0.

Este exercício ilustra, no nível dos microestados de um sistema, a razão pela qual a terceira lei da termodinâmica é cumprida.

- Exercício 2

Razão se a próxima declaração é verdadeira ou falsa:

"A entropia de um sistema na temperatura absoluta zero é exatamente zero".

Justifique a resposta e descreva alguns exemplos.

Solução

A resposta é: FALSO.

Antes de tudo, a temperatura absoluta não pode ser alcançada porque o princípio da incerteza de Heisenberg e a terceira lei da termodinâmica seria violada. 

É muito importante observar que, na terceira lei, não é dito o que acontece no absoluto 0, mas quando a temperatura é infinitamente próxima do absoluto 0. A diferença é sutil, mas significativa.

A terceira lei não afirma que, quando a temperatura leva um valor arbitrariamente próximo de zero absoluto, a entropia tende a zero. Isso aconteceria apenas no caso analisado anteriormente: o cristal perfeito, que é uma idealização.

Muitos sistemas de escala microscópica, ou seja, em escala quântica, têm seu nível de base energética degenerar, O que significa a existência de várias configurações no nível mais baixo de energia. 

O acima significa que nesses sistemas entropia nunca seria exatamente zero. A entropia também não seria exatamente zero em sistemas que são vitrificados quando a temperatura tende a zero absoluto. Nesse caso, o entropia residual Antes de ser visto.

É porque suas moléculas ficaram "presas" antes de ocuparem os níveis mais baixos de energia disponíveis, o que aumenta consideravelmente o número de microestados possíveis, impossibilitando que a entropia seja exatamente zero.

Referências

1. Cengel, e. 2012. Termodinâmica. 7ª edição. McGraw Hill. 347.
2. Laboratório de propulsão a jato. O ponto mais legal do universo. Recuperado de: Coldatomlab.JPL.Panela.Gov.
3. González, a. Entropia e espontaneidade. Recuperado de: geocidades.Ws
4. Quora. Qual é o uso prático da terceira lei da termodinâmica?. Recuperado de: Quora.com
5. Química Geral. Terceiro princípio da termodinâmica. Recuperado de: Corinto.PUCP.Edu.educaçao Fisica
6. Terceira Lei da Termodinâmica. Recuperado de: youtube.com
7. Wikipedia. Residual de entropia. Recuperado de: em.Wikipedia.com
8. Wikipedia. Terceira Lei da Termodinâmica. Recuperado de: em.Wikipedia.com