Teorema de Varignon

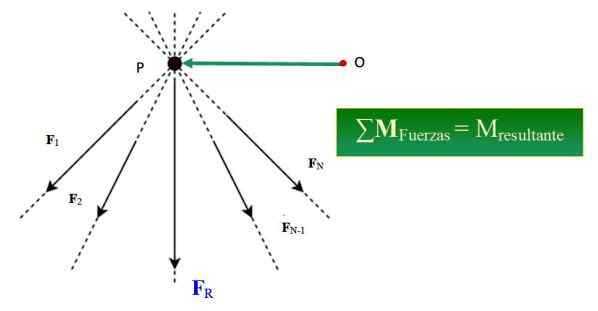
figura 1.- O teorema de Varignon afirma que a soma do momento das forças em torno de um certo ponto é equivalente ao tempo do resultado em relação a esse ponto. Fonte: Wikimedia Commons/F. Zapata.

Qual é o teorema de Varignon?

O teorema de Varignon, na mecânica, afirma que a soma dos momentos produzidos por um sistema de forças simultâneas em relação a um certo ponto é igual ao momento da força resultante em relação ao mesmo ponto.

Por esse motivo, este teorema também é conhecido como O começo dos momentos.

Enquanto o primeiro a afirmar que foi o holandês Simon Stevin (1548-1620), o criador do paradoxo hidrostático, o matemático francês Pierre Varignon (1654-1722) foi quem posteriormente lhe deu sua forma definitiva.

Um exemplo de como o teorema de Varignon funciona em mecânica é o seguinte: suponha que um sistema simples de dois coplanares e forças simultâneas atue em um ponto F₁ e F₂, (Indicado com negrito por seu personagem vetorial). Essas forças dão origem a uma força líquida ou resultante, chamada F_R.

Cada força exerce um torque ou momento em relação a um ponto ou, que é calculado pelo produto vetorial entre o vetor de posição r_Op e a força F, onde r_Op É direcionado de ou para o ponto de concordância P:

M_O1 = r_Op × F₁

M_O2 = r_Op × F₂

Dado que F_R = F₁ + F₂, então:

M_QUALQUER = r_Op × F₁ + r_Op × F₂ = M_O1 + M_O2

Mas como r_Op É um fator comum, então, aplicando propriedades distributivas ao produto cruzado:

M_QUALQUER = r_Op × (F₁ + F₂) = r_Op × F_R                

Portanto, a soma dos momentos ou torques de cada força em relação ao ponto ou é equivalente ao tempo da força resultante em relação ao mesmo ponto.

Declaração e demonstração

Ser um sistema de n forças simultâneas, formadas por F₁, F₂, F₃.. F_N, cujas linhas de ação são destinadas ao ponto P (veja a Figura 1), o momento deste sistema de forças M_QUALQUER, Sobre um ponto ou é dado por:

Pode servir a você: Equilíbrio instável: conceito e exemplos

M_QUALQUER = r_Op × F₁ + r_Op × F₂ + r_Op × F₃ +.. r_Op × F_N = r_Op × (F₁ + F₂ + F₃ +.. F_N)

Demonstração

Para demonstrar o teorema, a propriedade distributiva do produto vetorial entre vetores é feita.

Sejam as forças F₁, F₂, F₃.. F_N aplicado a pontos para₁, PARA₂, PARA₃… PARA_N e simultaneamente no ponto P. O momento resultante deste sistema, com relação a um ponto ou, chamado M_QUALQUER, É a soma dos momentos de cada força, com relação a esse ponto:

M_QUALQUER = ∑ r_OAI × F_Yo

Onde a soma vai de i = 1 a i = n, já que existem n forças. Como essas são forças simultâneas e, como o produto vetorial entre vetores paralelos é nulo, acontece que:

r_PAI × F_Yo = 0

Com o vetor nulo denotado como 0.

O momento de uma das forças em relação a, por exemplo, a da força F_Yo aplicado em a_Yo, se escreve assim:

M_ouvi = r_OAI × F_Yo

O vetor de posição r_OAI  Pode ser expresso como a soma da posição de dois vetores:

r_OAI = r_Op + r_PAI

Dessa maneira, o momento em relação ou força F_Yo é:

M_ouvi = (r_Op + r_PAI) × F_Yo = (r_Op × F_Yo) + (r_PAI × F_Yo)

Mas o último termo é nulo, como explicado acima, porque r_PAI está na linha de ação de F_Yo, portanto:

M_ouvi = r_Op × F_Yo

Sabendo que o momento do sistema em relação ao ponto ou é a soma de todos os momentos individuais de cada força em relação a esse ponto, então:

M_QUALQUER = ∑ M_ouvi = ∑ r_Op × F_Yo

Como r_Op É constante sai da soma:

M_QUALQUER = r_Op × (∑ F_Yo)

Mas ∑ F_Yo É simplesmente a rede ou força resultante F_R, Portanto, conclui -se imediatamente que:

Pode servir a você: Leyden Bottle: Peças, Operação, Experiências

M_QUALQUER = r_Op × F_R

Exemplo

O teorema de Varignon facilita o cálculo do momento da força F Em relação ao ponto ou estrutura mostrada na figura, se a força for dividida em seus componentes retangulares e o momento de cada um deles é calculado:

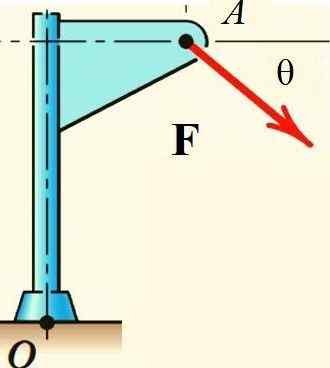Figura 2.- O teorema de Varignon se aplica para calcular o momento da força ao redor ou. Fonte: f. Zapata.

Aplicações do Teorema da Varignon

Quando a força resultante de um sistema é conhecida, o teorema de Varignon pode ser aplicado para substituir a soma de cada um dos momentos produzidos pelas forças que o compõem no momento do resultante.

Se o sistema consiste em forças no mesmo plano e o ponto em relação ao qual você deseja calcular o momento pertence a esse plano, o momento resultante é perpendicularmente.

Por exemplo, se todas as forças estiverem no plano XY, o momento é direcionado no eixo z e resta apenas sua magnitude e seu significado, esse é o caso do exemplo descrito acima.

Nesse caso, o teorema de Varignon permite calcular o momento resultante do sistema através do somatório. É muito útil no caso de um sistema de forças tridimensionais, para as quais a direção do momento resultante não é conhecida a priori.

Para resolver esses exercícios, é conveniente.

Exercício resolvido

Por teorema de Varignon, calcule o momento da força f ao redor do ponto ou mostrado na figura se a magnitude de f for 725 n.

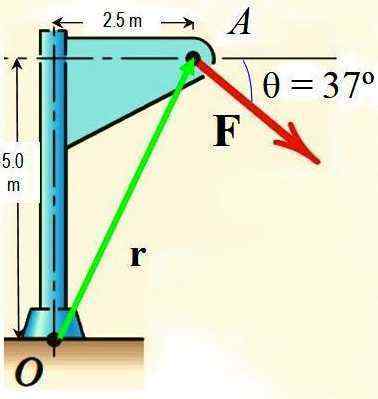Figura 3.- Figura para o exercício resolvido. Fonte: f. Zapata.

Solução

Para aplicar o teorema de Varignon, a força se decompõe F em dois componentes, cujos respectivos momentos ao redor ou são calculados e adicionados para obter o momento resultante.

Pode servir você: corpo rígido

F_x = 725 n ∙ cos 37 º = 579.0 n

F_e = - 725 n n ∙ sen 37 º = −436.3 n

Da mesma forma, o vetor de posição r Dirigido de ou para a tem os componentes:

r_x = 2.5m

r_e = 5.0 m

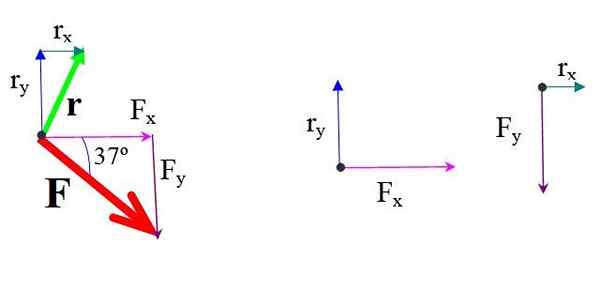Figura 4.- Componentes de força e posição. Fonte: f. Zapata.

O momento de cada componente da força em relação ou está multiplicando a força e a distância perpendicular.

Ambas as forças tendem a girar a estrutura na mesma direção, que neste caso é o sentido da pontuação, que é arbitrariamente atribuído sinal positivo:

M_Boi = F_x∙ r_e ∙ Sin 90º = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_e∙ r_x ∙ Sin (−90º) = −436.3 n ∙ 2.5 m ∙ (−1) = 1090.8 n ∙ m

O momento resultante em relação a ou é:

M_QUALQUER = M_Boi + M_Oy = 3985.8 n ∙ m perpendicular ao plano e em um torque.

Referências

1. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley. 
2. Cerveja, f. 2010. Estático. McGraw Hill. 9NA. Edição.
3. Hibbeler, R. 1992. Mecânica para engenheiros. 6º. Edição. CECSA.
4. Engenharia HK. Teorema de Varignon. Recuperado de: youtube.com.
5. Wikipedia. Teorema de Varignon (mecânica). Recuperado de: em.Wikipedia.org.