Teorema de Torricelli

Qual é o teorema de Torricelli?

Ele Teorema de Torricelli O Princípio de Torricelli afirma que a velocidade do líquido que sai através do buraco na parede de um tanque ou recipiente é idêntico ao qual um objeto adquire que é retirado livremente de uma altura igual à da superfície livre do líquido para O buraco.

O teorema é ilustrado na figura a seguir:

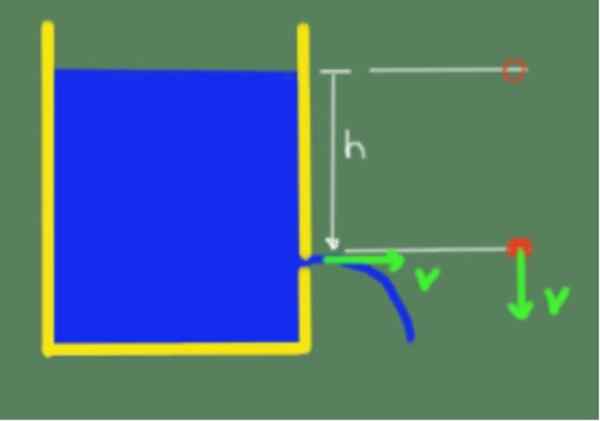Ilustração do teorema de Torricelli. Fonte: Self feito.

Devido ao teorema de Torricelli, podemos dizer que a velocidade de saída do líquido por um orifício que fica até a altura h abaixo da superfície livre do líquido é dada pela seguinte fórmula:

Onde g é a aceleração da gravidade e H é a altura do buraco para a superfície livre do líquido.

Evangelista Torricelli era um físico e matemático nascido na cidade de Faenza, Itália, em 1608. Torricelli é atribuído à invenção do barômetro Mercury e, em reconhecimento, há uma unidade de pressão chamada “Torr”, equivalente a um milímetro de mercúrio (mm de HG).

Demonstração do teorema

No teorema de Torricelli e na fórmula que dá a velocidade, assume que as perdas devido à viscosidade são desprezíveis, pois na queda livre é assumida que o atrito devido ao ar que circunda o objeto que cai é insignificante.

A suposição anterior é razoável na maioria dos casos e também implica a conservação da energia mecânica.

Para demonstrar o teorema, em primeiro lugar, encontraremos a fórmula de velocidade para um objeto que é liberado com zero rapidez inicial, da mesma altura que a superfície líquida no tanque.

Pode servir a você: ondas tridimensionais: conceito, tipos e exemplos

O princípio da conservação de energia será aplicado para obter a velocidade do objeto que cai exatamente quando uma altura caia h igual ao do buraco à superfície livre.

Como não há perdas de atrito, é válido aplicar o princípio da conservação de energia mecânica. Suponha que o objeto que cai tenha massa m e a altura h é medida a partir do nível de saída do fluido.

Objeto que cai

Quando o objeto é liberado de uma altura igual à da superfície livre do líquido, sua energia é apenas potencial gravitacional, pois sua velocidade é zero e, portanto, sua energia cinética é zero. O EP de energia potencial é dado por:

Ep = m g h

Quando fica em frente ao buraco, sua altura é zero, a energia potencial é zero, por isso só possui energia cinética CE dada por:

EC = ½ M V²

Como a energia é preservada EP = CE do que é obtido:

½ m v² = m g h

Limpar a velocidade v A fórmula de Torricelli é obtida:

Líquido que sai do buraco

Em seguida, encontraremos a velocidade de saída do líquido através do orifício, a fim de demonstrar que ele coincide com o que foi calculado para um objeto que cai livremente.

Para isso, contaremos com o princípio de Bernoulli, que nada mais é do que a conservação da energia aplicada aos fluidos.

O princípio de Bernoulli é formulado assim:

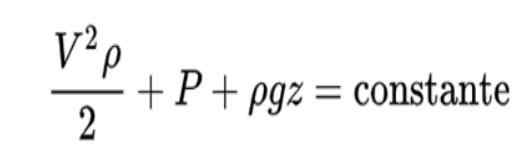
A interpretação desta fórmula é a seguinte:

• O primeiro termo representa a energia cinética do fluido por unidade de volume
• O segundo representa o trabalho realizado pela pressão por unidade de área transversal
• O terceiro representa energia potencial gravitacional por unidade de volume de fluido.

Pode atendê -lo: velocidade instantânea: definição, fórmula, cálculo e exercícios

À medida que começamos a partir da premissa que é um fluido ideal, em condições não violentas com velocidades relativamente baixas, é pertinente afirmar que a energia mecânica por unidade de volume no fluido é constante em todas as regiões ou seções transversais da mesma.

Nesta fórmula V é a velocidade do fluido, ρ Densidade de fluidos, P a pressão e z A posição vertical.

Na figura que aparece abaixo, a fórmula de Torricelli é demonstrada com base no princípio de Bernoulli.

Aplicamos a fórmula de Bernoulli na superfície livre do líquido que denotamos (1) e no orifício de saída que denotamos por (2). O nível de altura zero foi escolhido com o orifício de saída.

Sob a premissa de que a seção transversal em (1) é muito maior que em (2), podemos assumir que a velocidade de diminuição do líquido em (1) é praticamente negligenciada.

É por isso que V foi colocado₁= 0, a pressão à qual o líquido é submetido em (1) é a pressão atmosférica e a altura medida do buraco é h.

Para a seção de saída (2), assumimos que a velocidade de saída é V, a pressão à qual o líquido para a saída também é submetido é a pressão atmosférica e a altura da saída é zero.

Os valores correspondentes às seções (1) e (2) são substituídos na fórmula de Bernoulli e igual. A igualdade é válida porque assumimos que o fluido é ideal e não há perdas de atrito viscoso. Depois que todos os termos foram simplificados, a velocidade é obtida no orifício de saída.

Pode atendê -lo: anão vermelho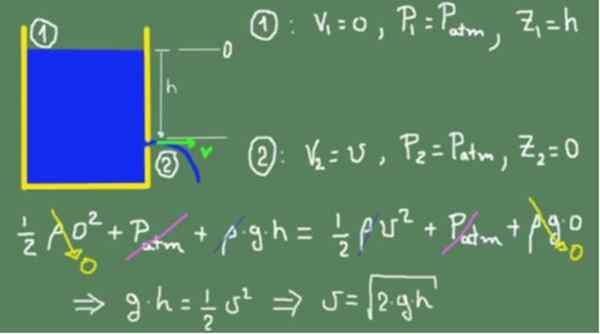

A caixa anterior mostra que o resultado obtido é o mesmo que o de um objeto que cai livremente,

Com o que é demonstrado o princípio de toricelli.

Exercícios resolvidos

Exercício 1

Yo) O pequeno tubo de saída de um tanque de água está 3 m abaixo da superfície da água. Calcule a velocidade da saída de água.

Solução:

A figura a seguir mostra como a fórmula de Torricelli é aplicada a este caso.

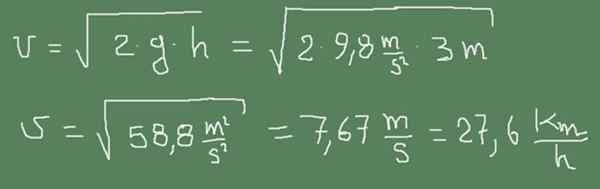
Exercício 2

Ii) Supondo que o tubo de saída do tanque de exercício anterior tenha um diâmetro de 1 cm, calcule o fluxo de saída de água.

Solução:

O fluxo é o volume de líquido que sai por unidade de tempo e é simplesmente calculado multiplicando a área do orifício de saída pela velocidade de saída.

A figura a seguir mostra os detalhes do cálculo.

Exercício 3

Iii) Determinar como a altura da superfície livre da água está em um recipiente se for conhecido

Que em um buraco na parte inferior do recipiente, a água chega a 10 m/s.

Solução:

Mesmo quando o buraco está na parte inferior do recipiente, a fórmula de Torricelli pode ser aplicada.

A figura a seguir mostra os detalhes dos cálculos.

Referências

1. Wikipedia. Teorema de Torricelli.
2. Hewitt, p. Ciência física conceitual. QUINTA EDIÇÃO.119.
3. Jovem, Hugh. 2016. Física da Universidade de Sears-Zansky com Física Moderna. 14ª ed. Pearson. 384.