Explicação do teorema da sobreposição, aplicações, exercícios resolvidos

Ele Teorema da superposição, Nos circuitos elétricos, estabelece que a tensão entre dois pontos, ou a corrente através deles, é a soma algébrica das tensões (ou das correntes, se for o caso), devido a cada fonte, como se cada um age em a maneira independente.

Este teorema permite analisar circuitos lineares contendo mais de uma fonte independente, pois é necessário apenas calcular a contribuição de cada.

A dependência linear é decisiva para o teorema aplicar. Um circuito linear é que cuja resposta é diretamente proporcional à entrada.

Por exemplo, a lei de Ohm aplicada a uma resistência elétrica estabelece que V = i.R, onde V É a tensão, R é a resistência e Yo É a corrente. É então uma dependência linear de tensão e corrente em uma resistência.

Nos circuitos lineares, o princípio da superposição é aplicado levando em consideração o seguinte:

-Cada fonte de tensão independente deve ser considerada separadamente e, para isso, é necessário desligar todos os outros. Basta colocar em 0 V todos aqueles que não estão em análise ou substituí -los no esquema por um curto -circuito.

-Se a fonte for, o circuito deve ser aberto.

-Quando a resistência interna das fontes de corrente e tensão é considerada, elas devem permanecer em vigor, fazendo parte do resto do circuito.

-Se houver fontes dependentes, elas devem ser como aparecem no circuito.

[TOC]

Formulários

O teorema da sobreposição é usado para obter circuitos mais simples e mais fáceis para lidar. Mas deve -se ter em mente que apenas se aplica àqueles com respostas lineares, conforme declarado no começo.

Em seguida, não pode ser usado diretamente para calcular o poder, por exemplo, uma vez que a energia está relacionada à corrente através:

P = i² R

Como a corrente é quadrada, a resposta não é linear. Nem é aplicável a circuitos magnéticos nos quais os transformadores intervêm.

Pode atendê -lo: eletricidade dinâmica

Por outro lado, o teorema da superposição oferece a oportunidade de conhecer o efeito que cada fonte no circuito tem. E, claro, por meio de sua aplicação, é possível resolvê -lo completamente, ou seja, conhecer correntes e tensões através de cada resistência.

O teorema da sobreposição também pode ser usado em conjunto com outros teoremas de circuito, por exemplo, o de Thévenin, para resolver configurações mais complexas.

Em circuitos atuais alternados, o teorema também é útil. Nesse caso, trabalhamos com impedâncias em vez de resistências, desde que a resposta total de cada frequência de independente possa ser calculada.

Finalmente, em sistemas eletrônicos, o teorema é aplicável para análise atual e alternativa, separadamente.

Etapas para aplicar o teorema de sobreposição

-Desativar todas as fontes independentes seguindo as instruções dadas no início, exceto a a ser analisada.

-Determinar a saída, tensão ou corrente, que produz essa fonte única.

-Repita as duas etapas descritas para todas as outras fontes.

-Calcule a soma algébrica de todas as contribuições encontradas nas etapas anteriores.

Exercícios resolvidos

Os exemplos resolvidos abaixo esclarecem o uso do teorema em alguns circuitos simples.

- Exemplo 1

No circuito mostrado na figura a seguir, encontre a corrente que atravessa cada resistência através do teorema de sobreposição.

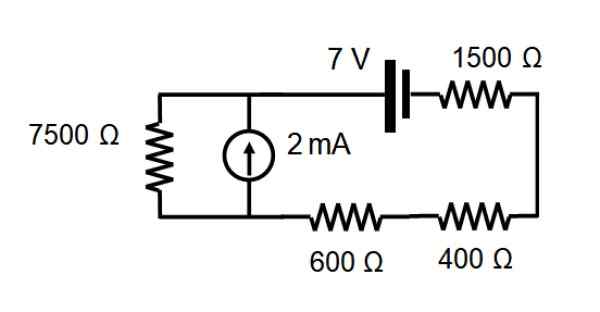
Solução

Contribuição da fonte de tensão

Para iniciar a fonte atual, é eliminado, com o qual o circuito permanece desta maneira:

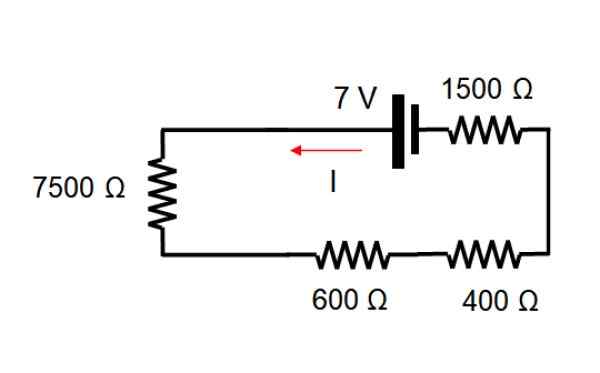
A resistência equivalente está adicionando o valor de cada resistência, pois estão todos em série:

7500 +600 +400 +1500 Ω = 10.000 Ω

Aplicando a lei de Ohm V = i.R E limpar a corrente:

I = v / r = 7/10.000 a = 0.0007 a = 0.7 MA

Esta corrente é a mesma para toda resistência.

Pode servir a você: Millikan Experiment: Procedimento, Explicação, Importância

Contribuição da fonte atual

A fonte de tensão é imediatamente eliminada, para trabalhar apenas com a fonte atual. O circuito resultante é mostrado abaixo:

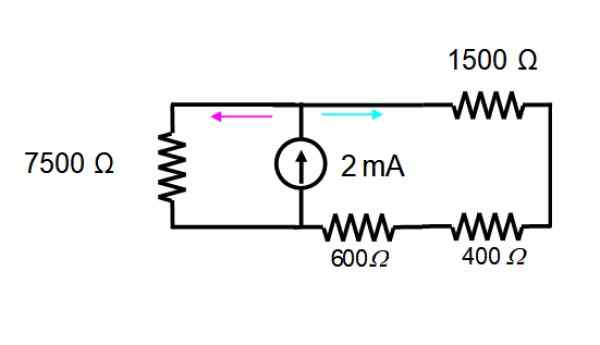
As resistências na malha à direita estão em série e podem ser substituídas por apenas uma:

600 +400 + 1500 Ω = 2500 Ω

O circuito resultante é assim:

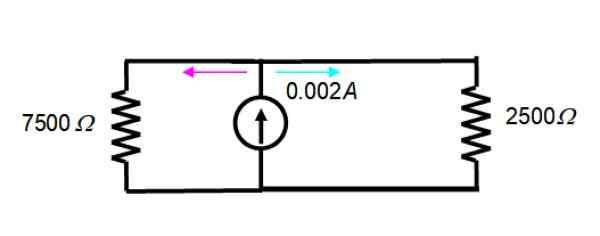
A corrente de 2 mA = 0.002 A é dividido entre as duas resistências da figura; portanto, a equação do divisor atual é válida:

Yo_x = (R_Eq/R_x) Yo_T

Onde Yo_x é a corrente em resistência R_x, R_Eq simboliza resistência equivalente e Yo_T é a corrente total. É necessário encontrar a resistência equivalente entre eles, sabendo que:

1/r_Eq = (1/ r₁) + (1/ r₂)

Portanto:

1/r_Eq = (1/7500) + (1/2500) = 1/1875 → R_Eq = 1875 Ω

Para este outro circuito, a corrente que passa pela resistência de 7500 Ω está substituindo os valores na equação divisória atual:

Yo_{7500 Ω} = (1875/7500). 0.002 a = 0.0005 a = 0.5 MA

Enquanto o que passa pela resistência de 2500 Ω é:

Yo_{2500 Ω} = 2 mA - 0.5 ma = 1.5 MA

Aplicativo do teorema do superposição

Agora, o teorema da sobreposição para cada resistência é aplicado, começando com os 400 Ω:

Yo_{400 Ω} = 1.5 mA - 0.7 ma = 0.8 ma

Importante: Para essa resistência, as correntes são subtraídas, à medida que circulam na direção oposta, como pode ser visto a partir da observação cuidadosa das figuras, nas quais os sentidos das correntes têm cores diferentes.

Essa mesma corrente vai igualmente para a resistência de 1500 Ω e 600 Ω, pois estão todos em série.

Em seguida, o teorema é aplicado para encontrar a corrente através da resistência de 7500 Ω:

Yo_{7500 Ω} = 0.7 ma + 0.5 ma = 1.2 MA

Importante: No caso da resistência de 7500 Ω, observe que as correntes são adicionadas, porque nos dois circuitos circula na mesma direção ao passar por essa resistência. Novamente, é necessário observar cuidadosamente os sentidos das correntes.

Pode servir a você: erro relativo: fórmulas, como é calculado, exercícios

- Exercício 2

Encontre a corrente e a tensão através da resistência de 12 Ω através do teorema de sobreposição.

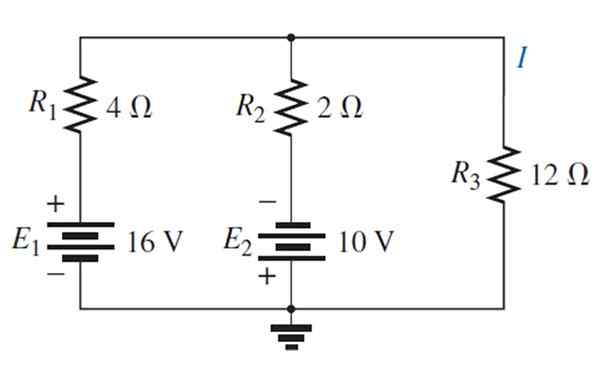
Solução

Fonte E é substituída₁ Com um curto -circuito:

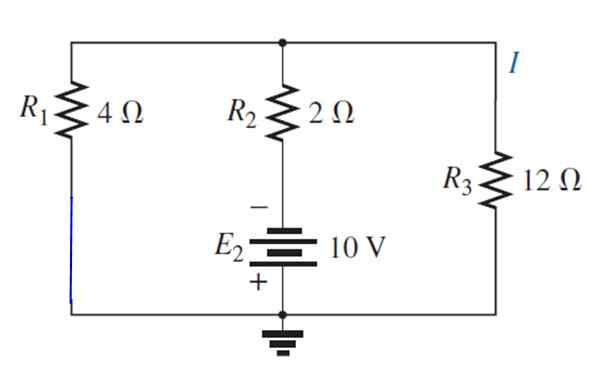
O circuito resultante é desenhado da seguinte maneira, para visualizar facilmente os resistores que permanecem em paralelo:

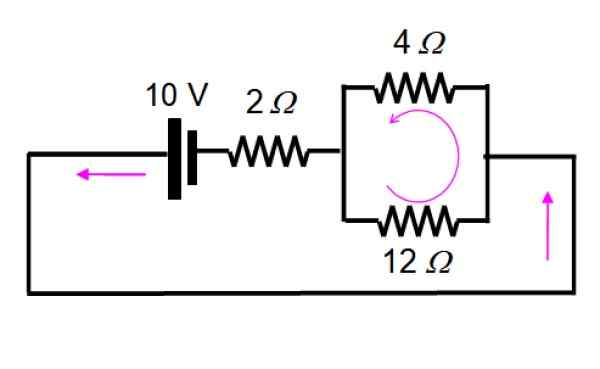
E agora é resolvido aplicando séries e paralelos:

1/r_Eq = (1/12) + (1/4) = 1/3 → R_Eq = 3 Ω

Essa resistência é por sua vez em série com a de 2 Ω, Portanto, a resistência total é 5 Ω. A corrente total é:

I = v / r = 10 v / 5 Ω = 2 a

Esta corrente é dividida como:

Yo_12Ω = (3/12) 2 a = 0.5 a

Portanto, a tensão é:

V_12Ω = 0.5 a × 12 Ω = 6 V

Agora a fonte está ativada₁:

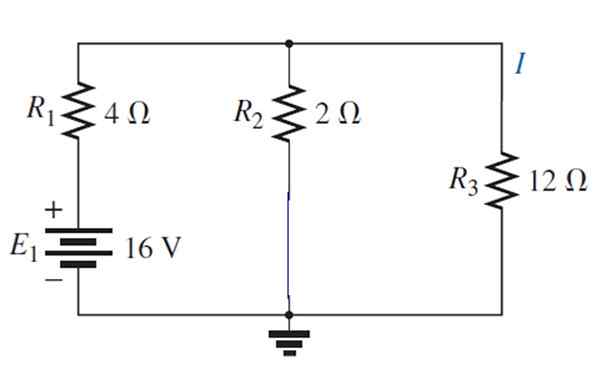
O circuito resultante pode ser desenhado dessa maneira:

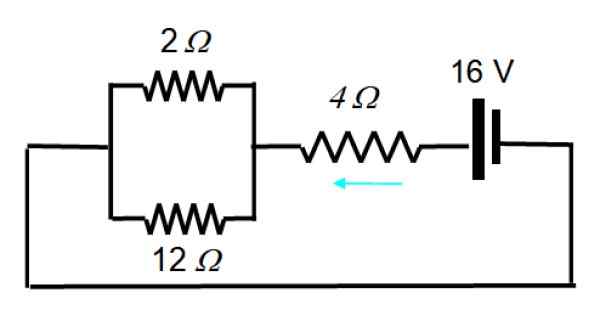
1/r_Eq = (1/12) + (1/2) = 7/12 → R_Eq = 12/7 Ω

E em série com o 4 Ω É uma resistência equivalente 40/7 Ω. Nesse caso, a corrente total é:

I = v/r = 16 v/(40/7) Ω = 14/5 a

O divisor de tensão com esses valores é aplicado novamente:

Yo_12Ω = ((12/7)/12) (14/5) a = 0.4 a

A corrente resultante é: 0.cinquenta.4 a = 0.1 a. Observe que eles foram subtraídos, porque a corrente de cada fonte faz significado diferente, como pode ser visto no circuito original.

A tensão através da resistência é:

V_12Ω = 0.4 a × 12 Ω = 4.8 v

Finalmente, a tensão total é: 6 V-4.8 V = 1.2 v

Referências

1. Alexander, c. 2006. Fundações de circuito elétrico. 3º. Edição. Mc Graw Hill.
2. Boylestad, r. 2011. Introdução à análise do circuito. 2º. Edição. Pearson.
3. Dorf, r. 2006. Introdução a circuitos elétricos. 7º. Edição. John Wiley & Sons.
4. Edminister, J. mil novecentos e noventa e seis. Circuitos elétricos. Série Schaum. 3º. Edição. Mc Graw Hill
5. Wikipedia. Divisor atual. Recuperado de: é.Wikipedia.org.