Propriedades da matriz ortogonal, demonstração, exemplos

Você tem um Matriz ortogonal Quando a matriz referida multiplicada por sua transposição resulta na matriz de identidade. Se o inverso de uma matriz for igual ao transposto, a matriz original é ortogonal.

Matrizes ortogonais são características de que o número de linhas seja igual ao número de colunas. Além.

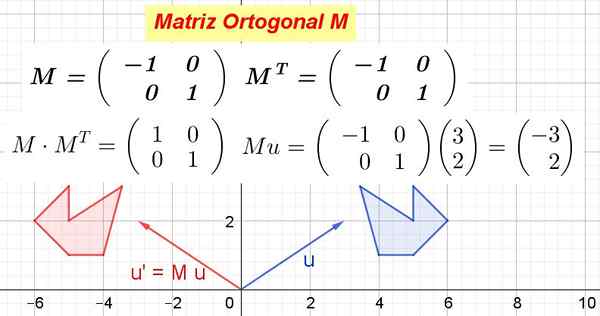figura 1. Exemplo de matriz ortogonal e como transforma objetos geométricos. (Preparado por Ricardo Pérez)

Quando uma matriz ortogonal é multiplicada pelos vetores de um espaço vetorial produz um Transformação isométrica, isto é, uma transformação que não muda as distâncias e preserva os ângulos.

Um representante típico das matrizes ortogonais é o matrizes de rotação. As transformações de matrizes ortogonais em um espaço vetorial são chamadas Transformações ortogonais.

As transformações geométricas de rotação e reflexão de pontos representados por seus vetores cartesianos são feitos aplicando matrizes ortogonais nos vetores originais para obter as coordenadas dos vetores transformados. É por esse motivo que as matrizes ortogonais são amplamente utilizadas no processamento gráfico computacional.

[TOC]

Propriedades

Uma matriz M É ortogonal se multiplicado por sua transposição M^T a matriz de identidade resulta em Yo. Da mesma forma, o produto da transposição de uma matriz ortogonal pela matriz original da matriz de identidade:

Milímetros^T = M^T M = i

Como conseqüência da declaração anterior, a transposição de uma matriz ortogonal é igual à sua matriz inversa:

M^T = M^-1.

O conjunto de matrizes de dimensão ortogonal n x n Eles formam o grupo ortogonal Ou (n). E o subconjunto de Ou (n) de matrizes ortogonais com determinação de +1 de Grupo de matrizes especiais é (n). Matrizes do grupo O seu n) São matrizes que produzem transformações de rotação lineares, também conhecidas como o Grupo de rotações.

Demonstração

Demonstraremos que uma matriz é ortogonal se, e somente se, os vetores da linha (ou vetores de coluna) são ortogonais entre si e da norma 1.

Pode servir você: Teorema de Bayes

Suponha que as fileiras de uma matriz ortogonal n x n são n n vetores ortonsoriais da dimensão n. Se for denotado por v1, v2,.. ., vn Os n vetores são cumpridos:

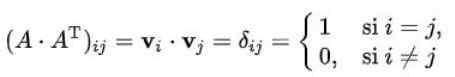
Onde é evidente que o conjunto de vetores de linha é um conjunto de vetores ortogonais com norma.

Exemplos

Exemplo 1

Mostre que a matriz 2 x 2 que o vetor tem em sua primeira linha V1= (-1 0) e em sua segunda linha o vetor V2= (0 1) é uma matriz ortogonal.

Solução: A matriz é construída M e sua transposição é calculada M^T:

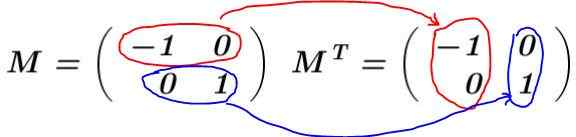
Neste exemplo, a matriz M É um carro transposto, ou seja, a matriz e sua transposição são idênticas. Multiplica M por sua transposição M^T:

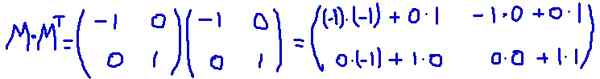
É verificado que M M^T É igual à matriz de identidade:

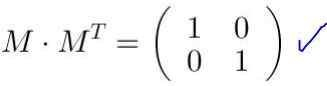
Quando a matriz M É multiplicado pelas coordenadas de um vetor ou de um ponto, são obtidas novas coordenadas que correspondem à transformação que a matriz faz no vetor ou no ponto.

A Figura 1 mostra como M Transforma o vetor ou em ou' E também como M Transforme o polígono azul no polígono vermelho. Como M É ortogonal, é então uma transformação ortogonal, que preserva distâncias e ângulos.

Exemplo 2

Suponha que você tenha uma matriz de 2 x 2 definida na reais dada pela seguinte expressão:

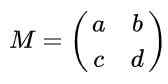
Encontre os valores reais de para, b, c e d para que a matriz M Ser uma matriz ortogonal.

Solução: Por definição, uma matriz é ortogonal se multiplicada por sua transposição é obtida como resultado da matriz de identidade. Lembrando que a matriz transposta é obtida do original, trocar linhas por colunas é a seguinte igualdade:

Pode servir a você: domínio e contradição de uma função (com exemplos)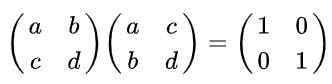

Executar a multiplicação da matriz é:

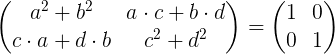
Igualando os elementos da matriz esquerda com os elementos da matriz de identidade à direita, obtemos um sistema de quatro equações com quatro incógnitas A, B, C e D.

Propomos para A, B, C e D as seguintes expressões baseadas em razões trigonométricas sinusas e cosseno:

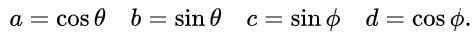
Com esta proposta e devido à identidade trigonométrica fundamental, a primeira e a terceira equação na igualdade dos elementos da matriz é automaticamente satisfeita. A terceira e a quarta equação são iguais e na igualdade matricular após a substituição dos valores propostos é assim:

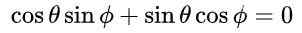
O que leva à seguinte solução:

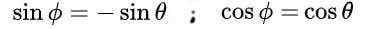
Finalmente, as seguintes soluções são obtidas para a matriz ortogonal M:

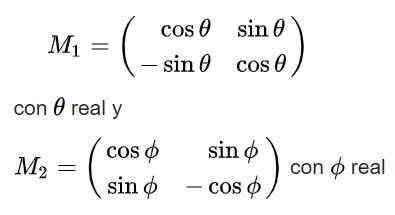
Observe que a primeira das soluções tem +1 determinante, por isso pertence ao seu grupo (2), enquanto a segunda solução possui um determinante -1 e, portanto, não pertence a este grupo.

Exemplo 3

Dada a seguinte matriz, encontre os valores de A e B para ter uma matriz ortogonal.

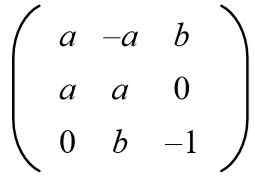
Solução: Para uma determinada matriz ser ortogonal, o produto com sua transposição deve ser a matriz de identidade. Em seguida, o produto Matrix da matriz fornecido com sua matriz transposta é feita dando o seguinte resultado:

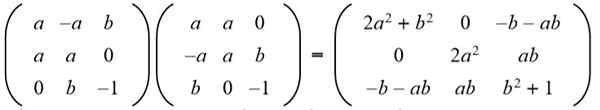
Em seguida, o resultado é comparado com a matriz de identidade 3 x 3:

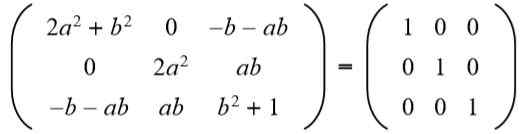
Na segunda linha, terceira coluna que você tem (A b = 0), mas para Não pode ser zero, porque se sim, a igualdade dos elementos da segunda linha e a segunda coluna não seria cumprida. Então necessariamente B = 0. Substituindo b Para o valor 0 que temos:

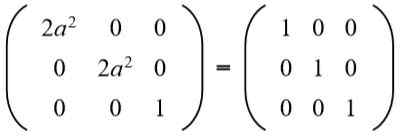
Então a equação é resolvida: 2a^2 = 1, cujas soluções são: +½√2 e -½√2.

Pode atendê -lo: tipos de ângulos, características e exemplos

Levando a solução positiva para para Isso resulta na seguinte matriz ortogonal:

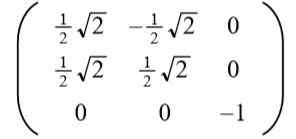
O leitor pode verificar facilmente se os vetores das linhas (e também vetores de coluna) são ortogonais e unitários, ou seja, Ortonormal.

Exemplo 4

Demonstrar que a matriz PARA cujas linhas são V1 = (0, -1 0), V2 = (1, 0, 0) e V3 = (0 0 -1) É uma matriz ortogonal. Além disso, encontre como os vetores da base canônica são transformados I j k Para os vetores U1, U2 e U3.

Solução: Deve -se lembrar que o elemento (i, j) de uma matriz multiplicada por sua transposição, é o produto escalar do vetor da linha (i) pela coluna (j) da transposição. Além disso, este produto é igual ao delta de Kronecker, caso a matriz seja ortogonal:

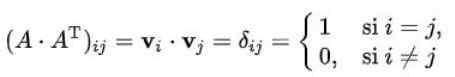
No nosso caso, é assim:

V1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • V2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Com o que é demonstrado que é uma matriz ortogonal.

Além do mais u1 = a i = (0, 1, 0); U2 = a j = (-1, 0, 0) e finalmente U3 = a k = (0, 0, -1)

Referências

1. Anthony Nicolaides (1994) Determinantes e matrizes. Pass Publicação.
2. Birkhoff e Maclane. (1980). Álgebra Moderna, Ed. Vicens-Vives, Madri.
3. Casteleiro Villalba m.  (2004) Introdução à Álgebra Linear. Editorial ESIC.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Matemática: Guia de sobrevivência de um aluno. Cambridge University Press.
6. Richard J. Brown (2012) Matemática de 30 segundos: as 50 teorias mais expandidas da mente em matemática. Ivy Press Limited.
7. Wikipedia. Matriz ortogonal. Recuperado de: é.Wikipedia.com
8. Wikipedia. Matriz ortogonal. Recuperado de: em.Wikipedia.com