Teorema da explicação de Steiner, aplicações, exercícios

Ele Teorema de Steiner, também conhecido como Teorema do eixo paralelo, Permite avaliar o momento de inércia de um corpo estendido, ao redor de um eixo paralelo a outro que passa pelo centro de massa do objeto.

Foi descoberto pela matemática suíça_Cm O momento de inércia do objeto em relação a um eixo que passa por seu CM e I Mass Center_z o momento da inércia em relação a outro eixo paralelo para este.

figura 1. Uma porta retangular que gira as alegrias tem um momento de inércia que pode ser calculado aplicando o teorema de Steiner. Fonte: Pixabay.

Conhecido a distância d que separa os dois eixos e a massa m do corpo em questão, o momento da inércia em relação ao eixo incógnito é:

Yo_z = I_Cm + MD²

O momento da inércia indica como é fácil para um objeto girar em torno de um determinado eixo. Depende não apenas do corpo do corpo, mas de como ele é distribuído. Por esse motivo, também é conhecido como Inércia rotacional, sendo suas unidades no sistema KG internacional . m².

O teorema mostra que o momento da inércia Yo_z É sempre maior que o momento da inércia Yo_Cm em um valor dado por M.D².

[TOC]

Formulários

Como um objeto é capaz de girar em torno de inúmeros eixos, e nas mesas geralmente apenas no momento da inércia em relação ao eixo que passa pelo centróide, o teorema de Steiner facilita o cálculo quando precisa girar corpos nos eixos em eixos que não coincidem com com com com com coincidência com com esse.

Pode servir a você: movimento retilíneo: características, tipos e exemplos

Por exemplo, uma porta geralmente não gira em torno de um eixo que passa por seu centro de massa, mas com relação a um eixo lateral, onde as dobradiças aderem.

Ao conhecer o momento da inércia, é possível calcular a energia cinética associada à rotação neste eixo. Sim K é energia cinética, Yo o momento da inércia ao redor do eixo em questão e Ω A velocidade angular é cumprida que:

K = ½ i.Ω²

Esta equação é muito semelhante à fórmula muito familiar de energia cinética para um objeto de massa M movendo -se em velocidade v:  K = ½ m.v². E é esse o momento da inércia ou inércia rotacional Yo desempenha em rotação o mesmo papel que a massa M Na tradução.

Demonstração do teorema de Steiner

O momento de inércia de um objeto estendido é definido como:

I = ∫r² Dm

Onde Dm É uma massa infinitesimal de massa e r É a distância entre Dm e o eixo de rotação z. Na Figura 2, este eixo atravessa o centro de massa cm, no entanto, pode ser qualquer um.

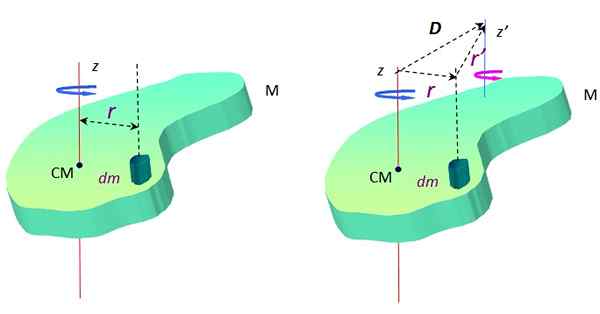Figura 2. Um objeto estendido em rotação em torno de dois eixos paralelos. Fonte: f. Zapata.

Em torno de outro eixo  z ', O momento da inércia é:

Yo_z= ∫ (R ')² Dm

Agora, de acordo com o triângulo formado pelos vetores D, r e R ' (Veja a Figura 2 à direita), há uma soma vetorial:

r + R ' = D   → R ' = D - r

Os três vetores estão no plano do objeto que pode ser o XY. A origem do sistema de coordenadas (0,0) é escolhida em cm para facilitar os cálculos a seguir.

Dessa maneira, o módulo quadrado do vetor R ' é:

Pode atendê -lo: biofísica: história, que estudos, aplicações, conceitos, métodos

(R ')² = (D_x- r_x)² +(D_e - r_e)² =

= D_x² + D_e² +r_x² + r_e2 -2d_xr_x - 2 d_er_e =

= D² + r²  - 2d_xr_x - 2 d_er_e

Agora esse desenvolvimento é substituído na integral do momento da inércia i_z e também a definição de densidade dm = ρ é usada.DV:

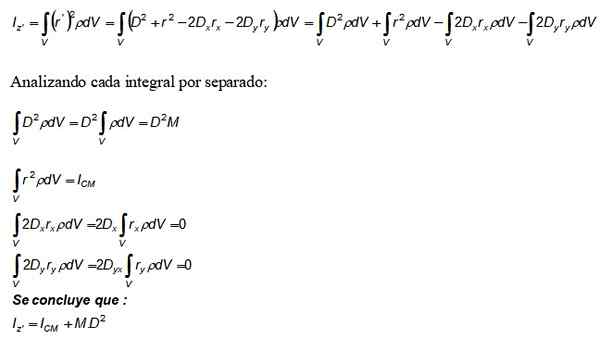
O termo m. D² que aparece no teorema de Steiner vem do primeiro integral, o segundo é o momento da inércia em relação ao eixo que passa pelo CM.

Por sua vez, o terceiro e o quarto integrais valem 0, pois, por definição, eles constituem a posição do CM, que foi escolhido como a origem do sistema de coordenadas (0,0).

Exercícios resolvidos

-Exercício resolvido 1

A porta retangular da Figura 1 tem uma massa de 23 kg, 1,30 de largura e 2,10 m de altura. Determine o momento de inércia da porta em relação ao eixo que passa pela alegria, assumindo que a porta é fina e uniforme.

Figura 3. Esquema para o exemplo resolvido 1. Fonte: Pixabay modificado.

Solução

De uma mesa de momentos de inércia, para uma placa retangular de massa m e dimensões para e b, O momento da inércia em relação ao eixo que passa pelo seu centro de massa é: i_Cm = (1/12)M(para² + b²).

Uma porta homogênea será assumida (uma abordagem, já que a porta da figura provavelmente não é tanto). Nesse caso, o centro de massa passa por seu centro geométrico. Na Figura 3, um eixo que passa pelo centro de massa foi desenhado e também é paralelo ao eixo que passa pela alegria.

Yo_Cm = (1/12) x 23 kg x (1.30²+2.10²) m² = 11.7 kg.m²

Pode atendê -lo: o que é um geoid?

Aplicando o teorema de Steiner para o eixo de rotação verde:

I = i_Cm + MD² = 11.7 kg.m² + 23 kg x 0.652 m² = 21.4 kg.

-Exercício resolvido 2

Encontre o momento de inércia de uma haste homogênea fina quando girar em relação a um eixo que passa por uma de suas pontas, veja a figura. É maior ou menor que o momento da inércia quando gira em torno de seu centro? Porque?

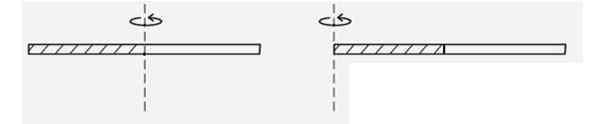Figura 4. Esquema para o exemplo resolvido 2. Fonte: f. Zapata.

Solução

De acordo com os momentos de inércia, o momento da inércia Yo_Cm de uma haste fina de massa M e comprimento eu é: Yo_Cm = (1/12) ml²

E o teorema de Steiner afirma que, quando é girado em torno de um eixo que passa por uma extremidade d = l/2 permanece:

I = i_Cm + MD² = (1/12) ml² + M (l/2)² = (1/3) ml²

Isso é velho.

A influência da distância no eixo de rotação não é linear, mas quadrática. Uma massa que é o dobro da distância que outra terá um momento de inércia proporcional a (2d)² = 4d².

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill. 313-340.
2. Universidade Estadual da Geórgia. Movimento rotacional. Recuperado de: Phys.NTHU.Edu.TW.
3. Teorema do eixo paralelo. Recuperado de: hiperfísica.Phy-Atr.GSU.Edu.
4. Rex, a. 2011. Fundamentos da Física. Pearson. 190-200.
5. Wikipedia. Teorema do eixo paralelo. Recuperado de: em.Wikipedia.org