Descrição do Teorema de Norton, Aplicativos, Exemplos e Exercícios

Ele Teorema de Norton, que se aplica a circuitos elétricos, estabelece que um circuito linear com dois terminais A e B pode ser substituído por outro completamente equivalente, consistindo em uma fonte atual chamada i_Não conectado em paralelo com uma resistência r_Não.

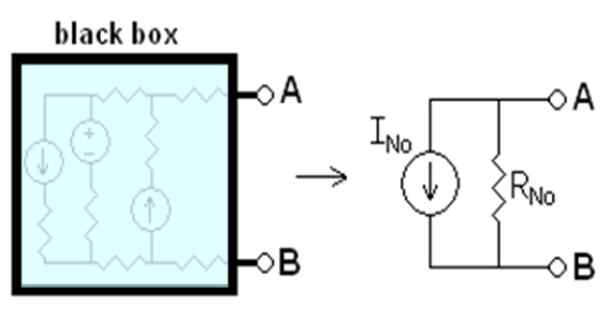
Disse o atual i_Não ouvi_N É o que fluiria entre os pontos A e B, se fossem curtos -circuitados. A resistência r_N É a resistência equivalente entre os terminais, quando todas as fontes independentes são desativadas. Tudo dito está esquematizado na Figura 1.

figura 1. Circuito equivalente de Norton. Fonte: Wikimedia Commons. Drumkid [CC BY-SA 3.0 (http: // criativecommons.Org/licenças/BY-SA/3.0/]]

A caixa preta na figura contém o circuito linear que será substituído por seu equivalente Norton. Um circuito linear é aquele em que a entrada e a saída têm uma dependência linear, como a relação entre a tensão V e a corrente direta i em um elemento ôhmico: v = i.R.

Essa expressão corresponde à lei de Ohm, onde r é resistência, que também pode ser uma impedância, se for um circuito de corrente alternado.

O teorema de Norton foi desenvolvido pelo eletricista e inventor Edward L Engineer. Norton (1898-1983), que trabalhou por um longo tempo para a Bell Laboratories.

[TOC]

Aplicativos do Teorema da Norton

Quando eles têm redes muito complicadas, com muitas resistência ou impedâncias e você deseja um circuito menor e mais gerenciável.

Dessa maneira, o teorema de Norton é muito importante ao projetar circuitos com vários elementos, bem como estudar sua resposta.

Relacionamento entre os teoremas de Norton e Thevenin

O teorema de Norton é o teorema da dupla Thevenin, o que significa que eles são equivalentes. O teorema de Thevenin indica que a caixa preta na Figura 1 pode ser substituída por uma fonte de tensão em série com uma resistência, chamada Thevenin R Resistance_º. Isso é expresso na figura a seguir:

Pode atendê -lo: mecânica de material: história, campo de estudo, aplicações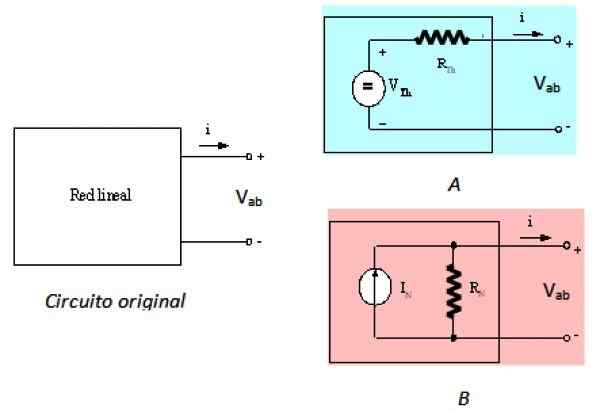 Figura 2. Circuito de esquerda original e seus equivalentes de Thévenin e Norton. Fonte: f. Zapata.

O circuito esquerdo é o circuito original, a rede linear na caixa preta, o circuito à direita é o equivalente a tevenina e o circuito B É equivalente de Norton, como descrito. Visto dos terminais A e B, os três circuitos são equivalentes.

Agora observe isso:

-No circuito original, a tensão entre os terminais é V_Ab.

-V_Ab  = V_º no circuito PARA

-Finalmente, v_Ab  = I_N.R_N no circuito B

Se os terminais A e B forem curto -circuito nos três circuitos, deve -se cumprir que a tensão e a corrente entre esses pontos devem ser os mesmos para os três, uma vez que são equivalentes. Então:

-No circuito original, a corrente é eu.

-Para o circuito A, a corrente é i = V_º / R_º, De acordo com a lei de Ohm.

-Finalmente no circuito B, a corrente é eu_N

Portanto, conclui -se que as resistências de Norton e Tevenina têm o mesmo valor e que a corrente é dada por:

i = i_N = V_º / R_º = V_º / R_N

Exemplo

Para aplicar corretamente o teorema de Norton, as seguintes etapas são seguidas:

-A seção do circuito para a qual o equivalente Norton será encontrada na rede é isolado da rede.

-No circuito restante, indique os terminais A e B.

-Substitua as fontes de tensão por circuitos curtos e atuais com circuitos abertos, para encontrar a resistência equivalente entre os terminais A e B. Isso é r_N.

-Retorne todas as fontes para suas posições originais, curto -circuito Os terminais A e B e encontre a corrente que circula entre eles. Este é eu_N.

Pode servir a você: Efeito Doppler: Descrição, Fórmulas, Casos, Exemplos

-Desenhe o circuito equivalente a Norton de acordo com o que é indicado na Figura 1. Ambos, a fonte atual e a resistência equivalente estão em paralelo.

Você também pode aplicar o teorema de Thevenin para encontrar r_º, que já sabemos ser igual a r_N, então pela lei de Ohm você pode encontrar eu_N E o circuito resultante é desenhado.

E agora vamos olhar para um exemplo:

Encontre o equivalente de Norton entre os pontos A e B do circuito a seguir:

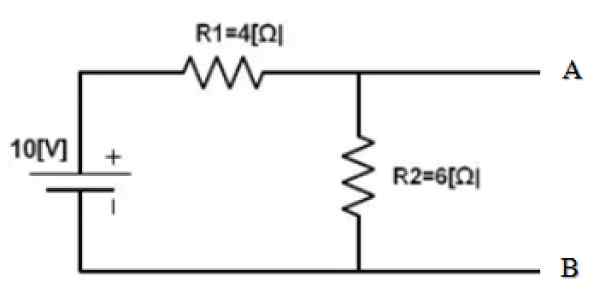Figura 3. Exemplo de circuito. Fonte: f. Zapata.

A parte do circuito já está isolada cujo equivalente deve ser encontrado. E os pontos A e B são claramente determinados. O que se segue é para curto -circuito a fonte de 10 V e encontrar a resistência equivalente do circuito obtido:

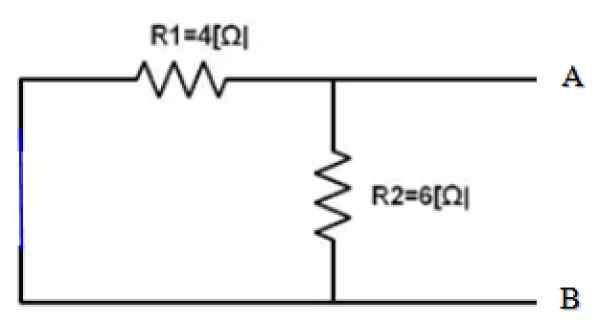Figura 4. Fonte de circuito curto. Fonte: f. Zapata.

Visualizações dos terminais A e B, ambas as resistências r₁ e r₂ Eles estão em paralelo, portanto:

1/r_Eq = 1/r₁₂ = (1/4) + (1/6) ω^-1 = 5/12 Ω^-1  → R_Eq = 12/5 Ω = 2.4 Ω

Então a fonte é devolvida ao seu lugar e os pontos A e B são curtos -circuitos para encontrar a corrente que circula lá, isso será_N. Em tal caso:

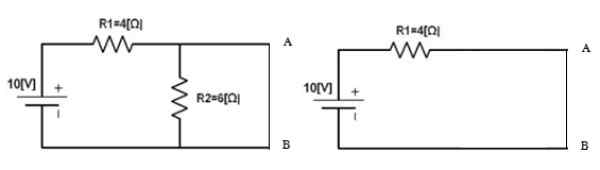Figura 5. Circuito para calcular a corrente Norton. Fonte: f. Zapata.

Yo_N = 10 v / 4 Ω = 2.5 a

Norton equivalente

Finalmente, o equivalente de Norton aos valores encontrados é desenhado:

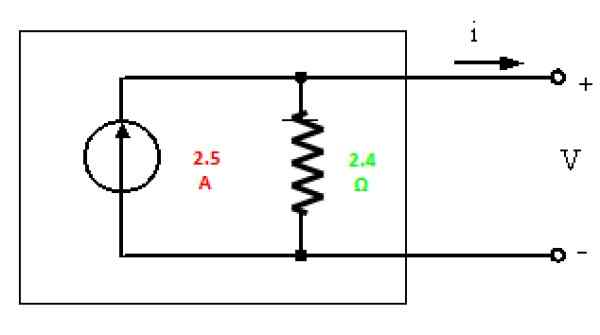Figura 6. Norton equivalente ao circuito na Figura 3. Fonte: f. Zapata.

Exercício resolvido

No circuito da figura a seguir:

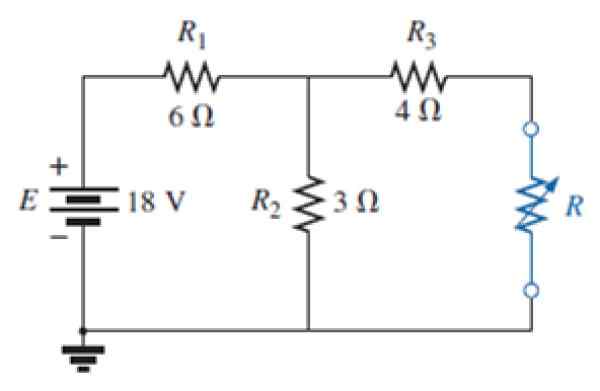Figura 7. Circuito para o exercício resolvido. Fonte: Alexander, C. 2006. Fundações de circuito elétrico. 3º. Edição. Mc Graw Hill.

a) Encontre o circuito equivalente de Norton da rede externa de resistência azul.

b) também encontre o equivalente de Thévenin.

Solução para

Seguindo as etapas indicadas acima, a fonte deve ser curta -circuito:

Pode servir a você: Difração do som: o que consiste em exemplos, aplicativos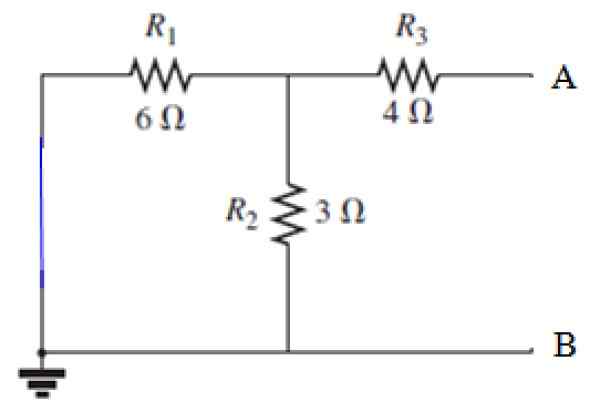 Figura 8. Fonte de circuito curto no circuito na Figura 7. Fonte: f. Zapata.

Cálculo de RN

Vista dos terminais A e B, Resistência R₃ está em série com o paralelo formado pelas resistências r₁ e r₂, Vamos primeiro calcular a resistência equivalente a este paralelo:

1/r₁₂ = (1/6)+ (1/3) ω^-1 = 1/2 Ω^-1  → R_Eq = 2/1 Ω = 2Ω

E então este paralelo está em série com r_3, para que a resistência equivalente seja:

R_Eq = 2 Ω + 4 Ω = 6 Ω

Este é o valor de ambos R_N a partir de r_º, como explicado antes.

Cálculo de in

Em seguida, os terminais A e B são curtos -circuitos, retornando a fonte ao seu lugar:

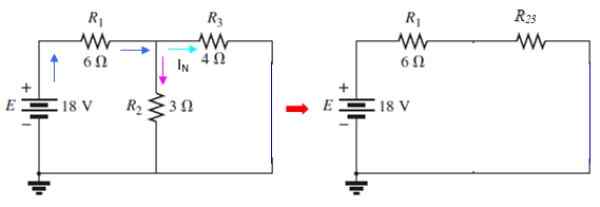Figura 9. Circuitos de corrente Norton. Fonte: f. Zapata.

A corrente passando por eu₃ é o atual eu_N procurado, que pode ser determinado com o método de malha ou usando série e paralelo. Neste circuito r₂ e r₃ Eles estão em paralelo:

1/r₂₃ = (1/3)+ (1/4) ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

A resistência r₁ É em série com este paralelo, então:

R₁₂₃ = 6 + (12/7) ω = 54/7 Ω

A corrente que sai da fonte (cor azul) é calculada pela lei de Ohm:

V = i. R → i = v/r = 18 v/(54/7 Ω) = 7/3 a

Esta corrente é dividida em duas partes: uma que cruza R₂ E outro que atravessa r₃. No entanto, a corrente que atravessa o paralelo r₂₃ É o mesmo que passa por r₁, como pode ser visto no circuito intermediário da figura. A tensão existe:

V₂₃ = I.R₂₃ = (7/3) A .(12/7) Ω = 4 V

Ambas as resistências r₂ e r₃ Eles estão nessa tensão, pois estão em paralelo, portanto:

Yo₃ = V₂₃ / R₃ = 4 v / 4 Ω = 1 a

Já temos a corrente Norton buscada, pois como disse anteriormente₃ = I_N, então:

Yo_N = 1 a

Norton equivalente

Tudo está pronto para desenhar o equivalente a Norton deste circuito entre os pontos A e B:

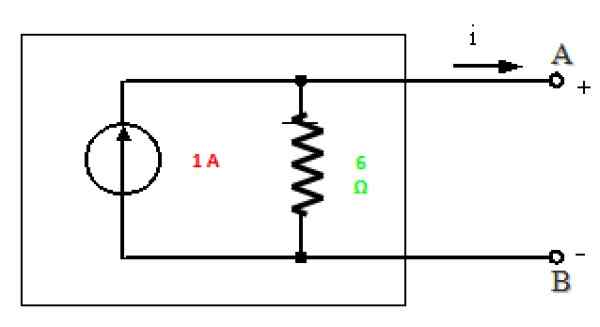Figura 10. Norton equivalente ao circuito na Figura 7. Fonte: f. Zapata.

Solução b

Encontrar o equivalente de Thévenin é muito simples, já que r_º = R_N= 6 Ω e conforme explicado nas seções anteriores:

V_º = I_N. R_N = 1 a . 6 Ω = 6 V

O circuito equivalente de Thévenin é:

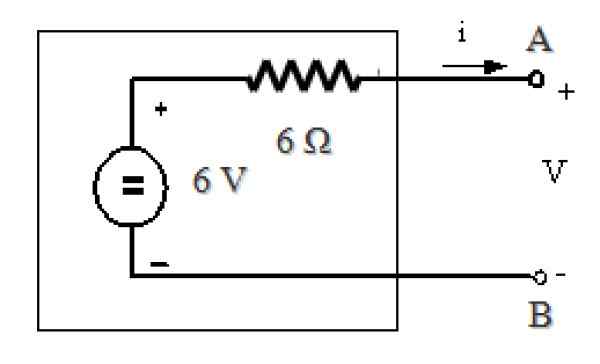Figura 11. O equivalente da tevenina do circuito na Figura 7. Fonte: f. Zapata.

Referências

1. Alexander, c. 2006. Fundações de circuito elétrico. 3º. Edição. Mc Graw Hill.
2. Boylestad, r. 2011. Introdução à análise do circuito. 2º. Edição. Pearson.
3. Dorf, r. 2006. Introdução a circuitos elétricos. 7º. Edição. John Wiley & Sons.
4. Edminister, J. mil novecentos e noventa e seis. Circuitos elétricos. Série Schaum. 3º. Edição. Mc Graw Hill.
5. Wikipedia. Teorema de Norton . Recuperado de: é.Wikipedia.org.