Teorema de Lamy

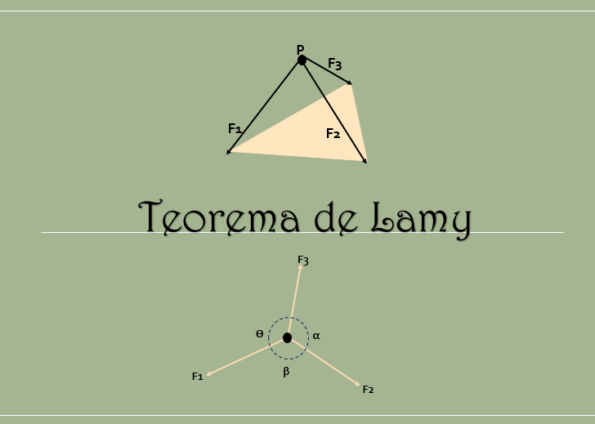
O teorema de Lamy estabelece que, quando um corpo rígido está em equilíbrio e na ação de três forças de dísticas (forças que estão no mesmo plano), suas linhas de ação concordam no mesmo ponto.

O teorema foi deduzido pelo físico francês e religioso. É amplamente usado para encontrar o valor de um ângulo, a linha de ação de uma força ou para formar o triângulo das forças.

Explicação

O teorema estabelece que, para que a condição de equilíbrio seja cumprida, as forças devem ser coplanares; isto é, a soma das forças exercidas em um ponto é zero.

Além disso, como visto na imagem a seguir, é cumprido que, ao prolongar as linhas de ação dessas três forças, elas concordam no mesmo ponto.

Assim, se três forças que estão no mesmo plano e simultâneas, a magnitude de cada força será proporcional ao seio do ângulo oposto, que são formadas pelas outras duas forças.

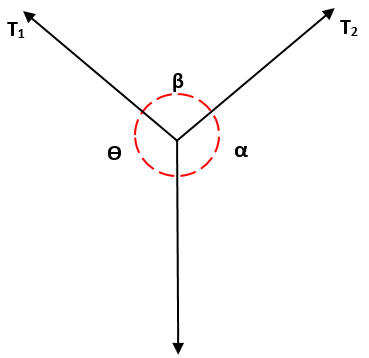
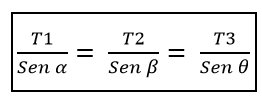
Isso tem que T1, a partir do peito de α, é igual à proporção de T2 / β, que por sua vez é igual à proporção de T3 / ɵ, ou seja::

A partir daí, segue -se que os módulos dessas três forças devem ser os mesmos se os ângulos que formam cada par de forças forem iguais a 120º.

Existe a possibilidade de que um dos ângulos seja obtuso (medida entre 90⁰ e 180⁰). Nesse caso, o peito desse ângulo será igual ao seio do ângulo suplementar (em seu par, mede 180⁰).

Exercício resolvido

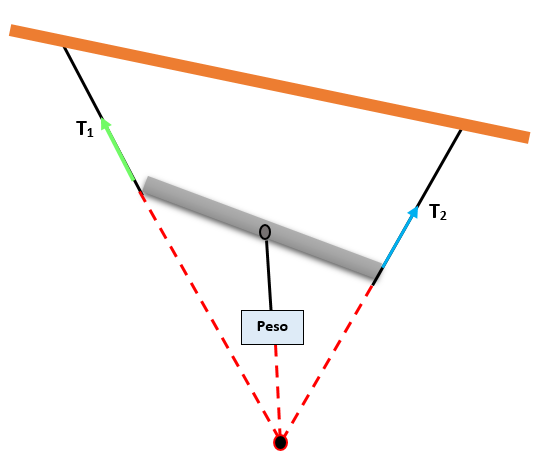
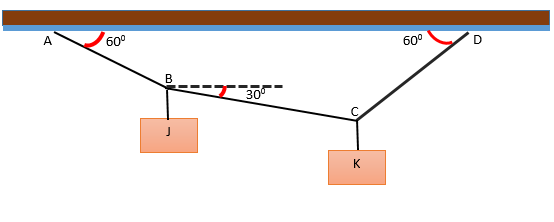
Há um sistema formado por dois blocos J ​​e K, que pendem em várias cordas que formam ângulos em relação à horizontal, como mostrado na figura. O sistema está em equilíbrio e o bloco J pesa 240 n. Determine o peso do bloco k.

Solução

Pelo princípio de ação e reação, as tensões exercidas nos blocos 1 e 2 serão iguais ao peso destes.

Agora um diagrama de corpo livre é construído para cada bloco e, assim, determinar os ângulos que formam o sistema.

Sabe -se que a corda que vai para A a B tem um ângulo de 30⁰ , de modo que o ângulo que complementa é igual a 60⁰ . Dessa forma, você atinge 90⁰.

Por outro lado, onde o ponto A está localizado, há um ângulo de 60⁰ Com relação à horizontal; O ângulo entre vertical e t_PARA Será = 180⁰ - 60⁰ - 90⁰ = 30⁰.

Assim, é obtido que o ângulo entre AB e BC = (30⁰ + 90⁰ + 30⁰) e (60⁰ + 90⁰ + 60) = 150⁰ e 210⁰. Ao ingressar, é verificado que o ângulo total é 360⁰.

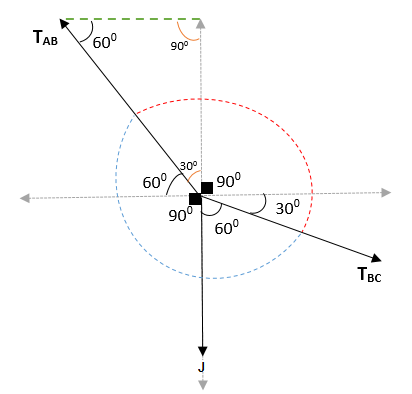
Aplicando o teorema de Lamy que você precisa:

T_Bc/ sin 150⁰ = P_PARA/ sin 150⁰

T_Bc = P_PARA

T_Bc = 240N.

No ponto C, onde está o bloco, o ângulo entre a horizontal e a corda BC é 30 é 30⁰, Portanto, o ângulo complementar é igual a 60⁰.

Por outro lado, há um ângulo de 60⁰ no ponto de CD; O ângulo entre vertical e t_C Será = 180⁰ - 90⁰ - 60⁰ = 30⁰.

Assim, obtém -se que o ângulo no bloco k é = (30⁰ + 60⁰)

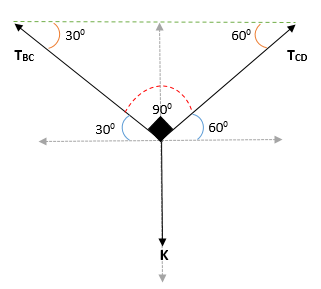
Aplicando o teorema de Lamy no ponto C:

T_Bc/ sin 150⁰ = B / sin 90⁰

Q = t_{BC *} Sen 90⁰ / sin 150⁰

Q = 240 n * 1/0,5

Q = 480 N.

Referências

1. Ferdinand p. Cerveja, e. R. (2013). Mecânica para engenheiros, estático. McGraw-Hill Interamerican.
2. Francisco Español, J. C. (2015). Problemas de álgebra linear resolvidos. Edições paraninfo, S.PARA.
3. Graham, j. (2005). Força e movimento. Houchton Mifflin Harcourt.
4. Harpe, p. d. (2000). Tópicos na teoria do grupo geométrico. University of Chicago Press.
5. P. Um tpler y, g. M. (2005). Física para Ciência e Tecnologia. Volume I. Barcelona: reverte você.PARA.