Teorema de Chebyshov isto é, aplicações e exemplos

Ele Teorema de Chebyshov (ou desigualdade de Chebyshov) é um dos resultados clássicos mais importantes da teoria da probabilidade. Ele permite estimar a probabilidade de um evento descrito em termos de uma variável aleatória x, fornecendo -nos um nível que não depende da distribuição da variável aleatória, mas da variação de x.

O teorema é chamado em homenagem à matemática russa.

Essa desigualdade, ou aqueles que, devido às suas características, são chamados de desigualdade de Chebyshov, é usada principalmente para aproximar probabilidades por meio de calcular níveis.

O que é o teorema de Chebyshov?

No estudo da teoria da probabilidade, acontece que, se a função de distribuição de uma variável aleatória x for conhecida, seu valor esperado poderá ser calculado - ou esperança matemática e (x) - e sua variância var (x), desde que estes existem valores. No entanto, recíproco não é necessariamente verdadeiro.

Isto é, conhecer e (x) e var (x) não pode necessariamente obter a função de distribuição de x, portanto, quantidades como p (| x |> k) para alguns k> 0, são muito difíceis de obter. Mas graças à desigualdade de Chebyshov, é possível estimar a probabilidade da variável aleatória.

O teorema de Chebyshov nos diz que, se tivermos uma variável aleatória x em um espaço de amostra com uma função de probabilidade P e se k> 0, então:

Pode atendê -lo: Acutangle Triangle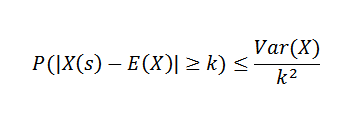

Aplicações e exemplos

Entre as muitas aplicações que o teorema de Chebyshov possui, o seguinte pode ser mencionado:

1. Limite de probabilidade

Esta é a aplicação mais comum e é usada para fornecer um nível superior para p (| x-e (x) | ≥k) onde k> 0, apenas com a variação e esperança da variável aleatória x, sem saber a função de probabilidade.

Exemplo 1

Suponha que o número de produtos fabricados em uma empresa por uma semana seja uma variável aleatória com uma média de 50.

Se se sabe que a variação de uma semana de produção é igual a 25, o que podemos dizer sobre a probabilidade de que esta semana a produção seja diferente de mais de 10 para a média?

Solução

Aplicando a desigualdade de Chebyshov que precisamos:

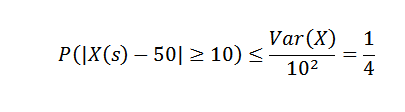
A partir disso, podemos obter que a probabilidade de que, na semana de produção, o número de itens exceda mais de 10 para a média é no máximo 1/4.

2. Demonstração de teoremas limitados

A desigualdade de Chebyshov desempenha um papel importante na demonstração dos teoremas dos limites mais importantes. Como exemplo, temos o seguinte:

Lei fraca de grandes números

Esta lei estabelece que dada uma sucessão x1, x2, ..., xn, ... de variáveis ​​aleatórias independentes com a mesma distribuição média e (xi) = μ e variância var (x) = σ², e uma amostra média conhecida de:

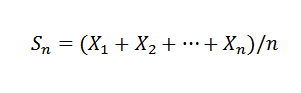
Então, para k> 0, você tem que:

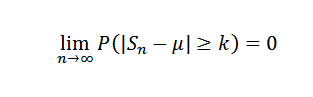
Ou equivalente:

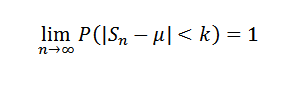
Demonstração

Primeiro notamos o seguinte:

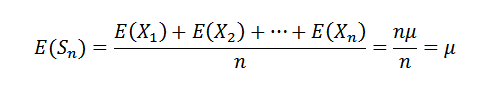
Como x1, x2, ..., xn são independentes, segue -se que:

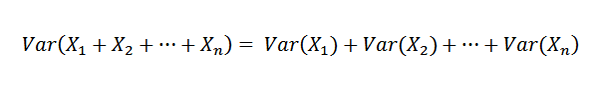
Portanto, é possível afirmar o seguinte:

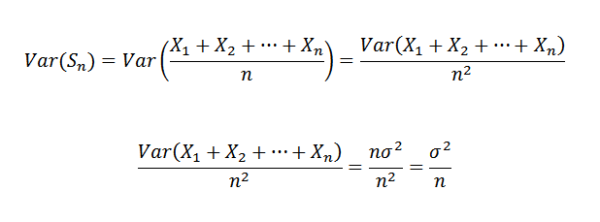
Então, usando o teorema de Chebyshov, você precisa:

Pode atendê -lo: funções trigonométricas: básico, no avião cartesiano, exemplos, exercícios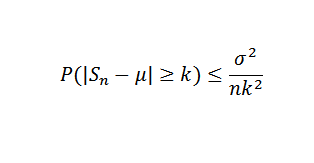

Finalmente, o teorema resulta do fato de que o limite certo é zero quando N tende ao infinito.

Deve -se notar que este teste foi feito apenas para o caso em que há a variação de Xi; isto é, não diverge. Assim, observamos que o teorema é sempre verdadeiro se E (xi) existir.

Teorema do limite de Chebyshov

Se x1, x2, ..., xn, ... é uma sucessão de variáveis ​​aleatórias independentes, de modo que haja alguns C0:

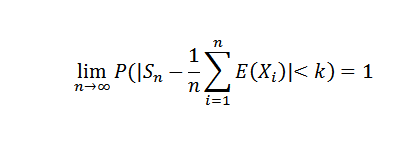
Demonstração

Como a sucessão de variações é uniformemente limitada, temos esse var (sn) ≤ c/n, para todos os n naturais n. Mas sabemos disso:

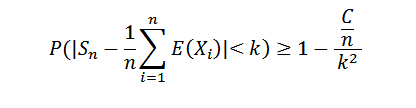
Fazendo n ao infinito, é o seguinte:

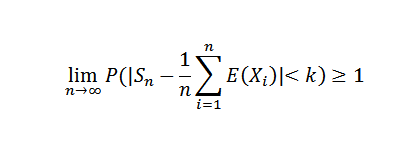
Como uma probabilidade não pode exceder o valor de 1, o resultado desejado é obtido. Como conseqüência desse teorema, poderíamos mencionar o caso particular de Bernoulli.

Si un experimento se repite n veces de forma independiente con dos resultados posibles (fracaso y éxito), donde p es la probabilidad de éxito en cada experimento y X es la variable aleatoria que representa el número de éxitos obtenidos, entonces para cada k>0 se tem que:

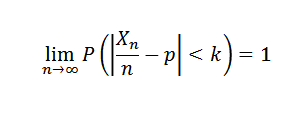
3. Tamanho da amostra

Em termos de variação, a desigualdade de Chebyshov nos permite encontrar um tamanho de amostra que seja suficiente para garantir que a probabilidade de que | média.

Precisamente, seja x1, x2, ... xn uma amostra de variáveis ​​aleatórias independentes de tamanho n e suponha que e (xi) = μ e sua variação σ². Então, devido à desigualdade de Chebyshov, você precisa:

Pode atendê -lo: Número ou Número e Número E: quanto ok, propriedades, aplicações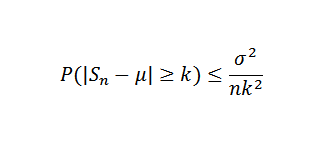

Agora seja Δ> 0 fixo. Temos que:

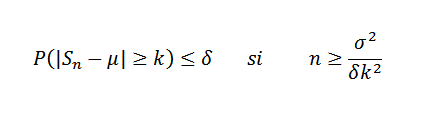
Exemplo

Suponha que x1, x2, ... xn sejam uma amostra de variáveis ​​aleatórias independentes com a distribuição de Bernoulli, para que eles assumam o valor 1 com probabilidade p = 0.5.

Qual deve ser o tamanho da amostra para garantir que a probabilidade de que a diferença entre a média aritmética SN e seu valor esperado (que exceda mais de 0,1) seja menor ou igual a 0.,01?

Solução

Temos que (x) = μ = p = 0,5 e qual var (x) = σ²= P (1-p) = 0,25. Para a desigualdade de Chebyshov, para qualquer K> 0, temos que:

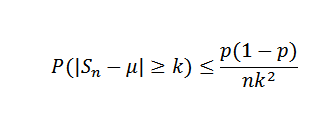
Agora, tomando k = 0,1 e δ = 0,01, você precisa:

Dessa maneira, conclui -se que é necessário um tamanho de amostra de pelo menos 2500 para garantir que a probabilidade do evento | Sn - 0,5 |> = 0,1 seja menor que 0,01.

Desigualdades do tipo Chebyshov

Existem várias desigualdades relacionadas à desigualdade de Chebyshov. Um dos mais conhecidos é a desigualdade de Markov:

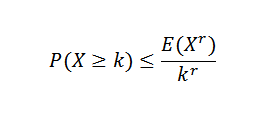
Nesta expressão x é uma variável aleatória não negativa com k, r> 0.

A desigualdade de Markov pode assumir formas diferentes. Por exemplo, ou uma variável aleatória não negativa (então p (y> = 0) = 1) e suponha que E (y) = μ exista. Suponha também que (e (y))^r= μ_r Há para algum número inteiro r> 1. Então:

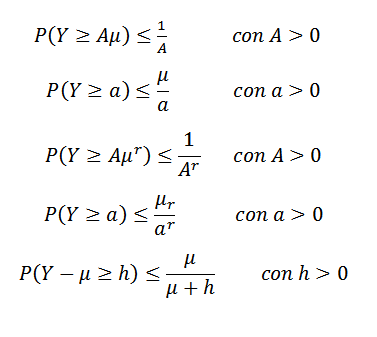
Outra desigualdade é a de Gauss, que nos diz que, dada uma variável aleatória unimodal x com moda em zero, então para k> 0,