Teorema de Bolzano

Explicamos qual é o teorema de Bolzano, suas aplicações e colocamos exercícios resolvidos

Qual é o teorema de Bolzano?

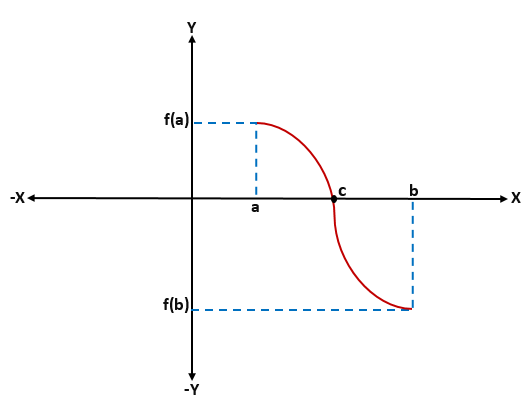
Ele Teorema de Bolzano Ele estabelece que, se uma função for contínua em todos os pontos de um intervalo fechado [a, b] e é cumprido que a imagem de "a" e "b" (sob a função) tem sinais opostos, então haverá pelo menos Um ponto "C" no intervalo aberto (a, b), de modo que a função avaliada em "C" seja igual a 0.

Este teorema foi declarado pelo filósofo, teólogo e matemático Bernard Bolzano em 1850. Este cientista, nascido na atual República Tcheca, foi uma das primeiras matemática da história a fazer uma demonstração formal das propriedades das funções contínuas.

Explicação do teorema

O teorema de Bolzano também é conhecido como o teorema dos valores intermediários, o que ajuda a determinar valores específicos, particularmente zeros, de certas funções reais de uma variável real.

Em uma determinada função f (x) continua -isto é, que f (a) e f (b) são conectados por uma curva-, onde f (a) está abaixo do eixo x (é negativo) e f (b) No acima do eixo x (é positivo) ou vice -versa, haverá um ponto de corte no eixo x que representará um valor intermediário "C", que estará entre "A" e "B", e o valor de f (c) será igual a 0.

Ao analisar graficamente o teorema de Bolzano, pode -se saber que, para qualquer função f contínua definida em um intervalo [a, b], onde f (a)_*f (b) é menor que 0, haverá pelo menos uma raiz "c" dessa função dentro do intervalo (a, b).

Este teorema não estabelece o número de pontos existentes nesse intervalo aberto, afirma apenas que há pelo menos 1 ponto.

Demonstração do teorema de Bolzano

Para demonstrar o teorema de Bolzano, é assumido sem perda de generalidade que f (a) 0; Dessa maneira, pode haver muitos valores entre "a" e "b" para os quais f (x) = 0, mas é necessário apenas demonstrar que existe um.

Pode atendê -lo: números imaginários: propriedades, aplicações, exemplos

Começa a avaliar f no ponto médio (a+b)/2. Se f ((a+b)/2) = 0, o teste termina aqui; Caso contrário, então f ((a+b)/2) é positivo ou negativo.

Uma das metades do intervalo [a, b] é escolhida, de modo que os sinais da função avaliada nas extremidades sejam diferentes. Este novo intervalo será [A1, B1].

Agora, se f avaliado no ponto médio de [A1, B1] não for zero, a mesma operação é realizada antes; Isto é, metade desse intervalo que atende à condição dos sinais é escolhido. Seja este novo intervalo [A2, B2].

Se esse processo continuar, haverá duas sucessões an e bn, de modo que:

an está crescendo e bn está diminuindo:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. . ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

Se o comprimento de cada intervalo [ai, bi] for calculado, você terá que::

B1-A1 = (B-A)/2.

B2-A2 = (B-A)/2².

.. .

bn-an = (b-a)/2^n.

Portanto, o limite quando n tende à infinidade de (Bn-An) é igual a 0.

O uso disso an está crescendo e limitado e bn está diminuindo e limitado, há um valor "c" de modo que:

a ≤ a1 ≤ a2 ≤ ... ≤ an ≤ .. .≤ c ≤ .. . ≤ bn ≤ .. . ≤ b2 ≤ b1 ≤ b.

O limite do limite é "c" e o limite de bn também é "c". Portanto, dado qualquer Δ> 0, sempre há um "n" de modo que o intervalo [an, bn] esteja contido no intervalo (c-δ, c+δ).

Agora, deve -se mostrar que f (c) = 0.

Se f (c)> 0, então f é contínuo, há um ε> 0 tal que f é positivo ao longo do intervalo (c -ε, c+ε). No entanto, como afirmado acima, existe um valor "n" que f altera a assinatura [an, bn] e, além disso, [an, bn] está contido em (c -ε, c+ε), o que é o que é uma contradição.

Se f (c) 0 tal que f é negativo ao longo do intervalo (c -ε, c+ε); Mas há um valor "n" que f muda de sinal [an, bn]. Acontece que [um, bn] está contido em (c -ε, c+ε), que também é uma contradição.

Pode atendê -lo: sinais de agrupamento

Portanto, f (c) = 0 e é isso que queria ser demonstrado.

Qual é o teorema de Bolzano para?

De sua interpretação gráfica, o teorema de Bolzano é usado para encontrar raízes ou zeros em uma função contínua, através da bisensão (abordagem), que é um método de pesquisa incremental que sempre divide os intervalos em 2.

Assim, se a função muda de sinal em um intervalo, a função f será avaliada no ponto médio, que é expresso da seguinte forma: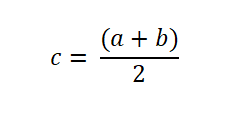A raiz é encontrada quando f (c) = 0. Caso contrário, o sinal de f (c) é analisado para determinar se se opõe ao sinal de f (a) ou o de f (b).

Então, um intervalo [a, c] ou [c, b] é levado onde ocorre a mudança de sinal e o processo é repetido até que o intervalo seja cada vez menor, a fim de se aproximar do valor que você deseja; isto é, para o valor que a função faz 0.

Em resumo, para aplicar o teorema de Bolzano e, assim, encontrar as raízes, limitar os zeros de uma função ou dar uma solução para uma equação, as seguintes etapas são executadas:

1. É verificado se f é uma função contínua no intervalo [a, b].
2. Se o intervalo não for dado, é preciso encontrar um onde a função seja contínua.
3. É verificado se as extremidades do intervalo darem sinais opostos quando avaliados em f.
4. Se sinais opostos não forem obtidos, o intervalo deve ser dividido em dois subintervalas usando o ponto médio.
5. Avalie a função no ponto médio e verifique se a hipótese de Bolzano é cumprida, onde f (a) _* f (b) < 0.
6. Dependendo do sinal (positivo ou negativo) do valor encontrado, o processo é repetido com um novo subinterval até que a hipótese mencionada seja atendida.

Pode atendê -lo: programação não linear: métodos e exercícios

Exercícios resolvidos

Exercício 1

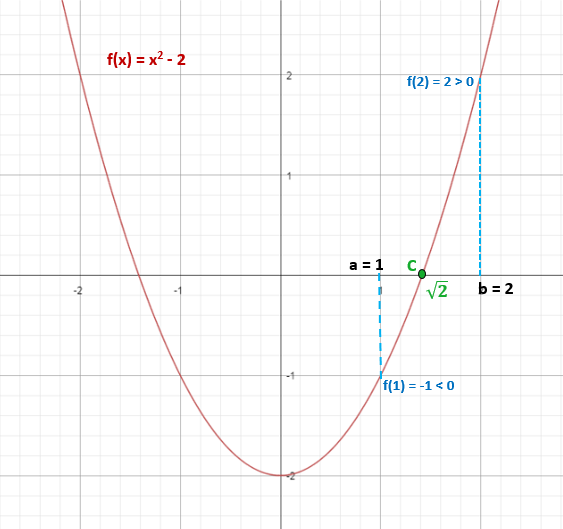
Determine se a função f (x) = x² - 2, tem pelo menos uma solução real no intervalo [1,2].

Solução

Você tem a função f (x) = x² - 2. Como é polinomial, significa que é contínuo em qualquer intervalo.

É solicitado a determinar se possui uma solução real no intervalo [1, 2], então agora você só precisa substituir as extremidades do intervalo na função para saber o sinal destes e saber se eles atendem à condição de ser diferente:

f (x) = x² - 2

f (1) = 1² - 2 = -1 (negativo)

f (2) = 2² - 2 = 2 (positivo)

Portanto, sinal de f (1) ≠ signo f (2).

Isso garante que haja pelo menos um ponto "c" que pertence ao intervalo [1,2], no qual f (c) = 0.

Nesse caso, o valor "C" pode ser calculado facilmente da seguinte maneira:

x² - 2 = 0

x = ± √2.

Assim, √2 ≈ 1.4 pertence ao intervalo [1,2] e cumpre que f (√2) = 0.

Exercício 2

Demonstrar que a equação x⁵ + x + 1 = 0 tem pelo menos uma solução real.

Solução

Primeiro, observamos que f (x) = x⁵ + X + 1 é uma função polinomial, o que significa que é contínua em todos os números reais.

Nesse caso, nenhum intervalo é dado, portanto, você deve escolher valores intuitivamente, de preferência perto de 0, para avaliar a função e encontrar as mudanças de sinal:

Se o intervalo [0, 1] for usado, ele deve::

f (x) = x⁵ + x + 1.

f (0) = 0⁵ + 0 + 1 = 1> 0.

f (1) = 1⁵ + 1 + 1 = 3> 0.

Como não há mudança de sinal, o processo é repetido com outro intervalo.

Se o intervalo [-1, 0] for usado, você deve::

f (x) = x⁵ + x + 1.

f (-1) = (-1)⁵ + (-1) + 1 = -1 < 0.

f (0) = 0⁵ + 0 + 1 = 1> 0.

Nesse intervalo, há uma mudança de sinal: sinal de f (-1) ≠ signo de f (0), o que significa que a função f (x) = x⁵ + X + 1 tem pelo menos uma raiz real “C” no intervalo [-1, 0], de modo que f (c) = 0. Em outras palavras, é verdade que x⁵ + x + 1 = 0 tem uma solução real no intervalo [-1,0].