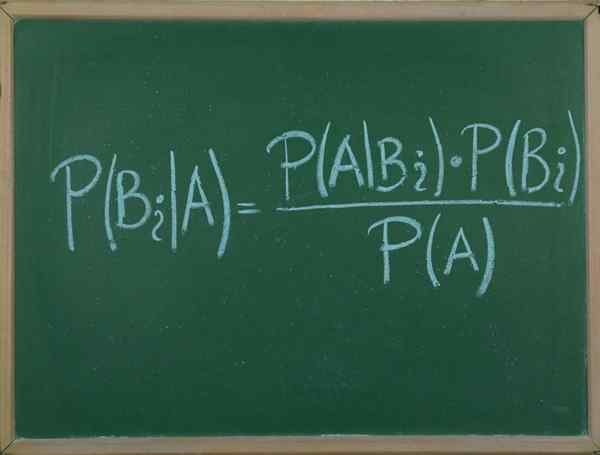Teorema de Bayes
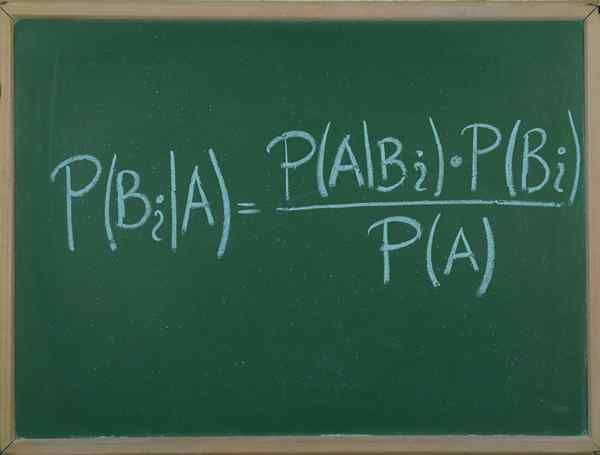
- 2062
- 121
- Dennis Heidenreich
Explicamos o que é o teorema de Bayes, suas aplicações e colocamos exercícios resolvidos
Qual é o teorema de Bayes?
Ele Teorema de Bayes É um procedimento que nos permite expressar a probabilidade condicional de um evento aleatório A DICE B, em termos da distribuição de probabilidade do evento B dado e da distribuição de probabilidade de apenas para.
Esse teorema é muito útil, pois, graças a ele, podemos relacionar a probabilidade de que um evento A aconteça sabendo que B estava acontecendo, com a probabilidade de ocorrer o oposto.
O teorema de Bayes era uma proposta de prata do reverendo Thomas Bayes, um teólogo inglês do século XVIII que também era matemático. Ele foi o autor de vários empregos em teologia, mas atualmente é conhecido por alguns tratados matemáticos, entre os quais o teorema de Bayes já mencionado como resultado principal.
Bayes lidou com esse teorema em uma obra intitulada "Um ensaio para resolver um problema na doutrina das chances" (um ensaio para resolver um problema na doutrina das possibilidades), publicada em 1763 e em que grandes desenvolveram estudos com aplicações com aplicações Em várias áreas de conhecimento.
Explicação
Primeiro, para uma maior compressão desse teorema, são necessárias algumas noções básicas de teoria de probabilidade, especialmente o teorema da multiplicação para a probabilidade condicional, que estabelece que
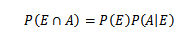
Para E e para eventos arbitrários de um espaço de amostra S.
E a definição de partições, que nos diz que temos1 ,PARA2,… , PARAn eventos de um espaço de amostra, eles formarão uma partição de s, se o aYo Eles são mutuamente exclusivos e sua união é S.
Pode atendê -lo: quais são os números para? Os 8 principais usosTendo isso, seja outro evento. Para que possamos ver B como
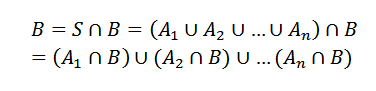
Onde umYo cruzado com b são eventos mutuamente exclusivos.
E, consequentemente,
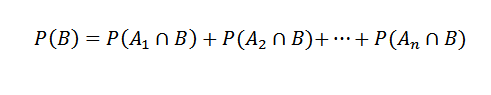
Em seguida, aplicando o teorema da multiplicação
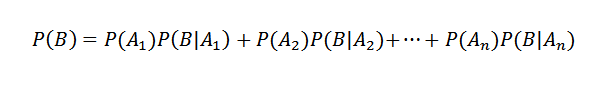
Por outro lado, a probabilidade condicional de AI B é definida por
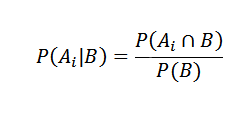
Substituindo corretamente, temos isso para qualquer eu
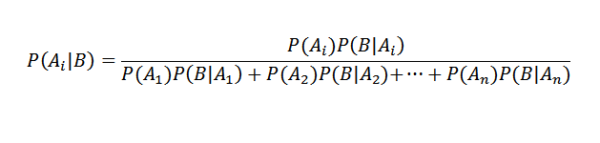
Aplicativos de Teorema de Bayes
Graças a esse resultado, grupos de pesquisa e diversas empresas conseguiram melhorar os sistemas baseados no conhecimento.
Estudo da doença
Por exemplo, no estudo de doenças, o teorema de Bayes pode ajudar a discernir a probabilidade de que uma doença seja encontrada em um grupo de pessoas com uma determinada característica, tomando como dados as taxas globais da doença e a predominância das referidas características em ambos Pessoas saudáveis e doentes.
Desenvolvimento de software
Por outro lado, no mundo das altas tecnologias, influenciou grandes empresas que se desenvolveram, graças a esse resultado, software "baseado no conhecimento".
Como exemplo diário, temos o Microsoft Office Assistant. O teorema de Bayes ajuda o software a avaliar os problemas que o usuário apresenta e determinar que conselhos fornecer e, assim, poder oferecer um serviço melhor de acordo com os hábitos do usuário.
Deve -se notar que essa fórmula foi ignorada até os últimos tempos, isso ocorre principalmente porque quando esse resultado foi desenvolvido há 200 anos, havia pouco uso prático para eles. No entanto, em nosso tempo, graças aos grandes avanços tecnológicos, os cientistas alcançaram maneiras de colocar esse resultado em prática.
Exercícios resolvidos
Exercício 1
Uma empresa de telefonia celular tem duas máquinas A e B. 54% dos telefones celulares são fabricados pela máquina A e o restante pela máquina B. Nem todos os telefones celulares estão em boas condições.
Pode atendê -lo: fatorizaçãoA proporção de telefones celulares defeituosos fabricados por A é 0.2 e para B é 0.5. Qual é a probabilidade de que um telefone celular da referida fábrica esteja com defeito? Qual é a probabilidade de que, saber que um telefone celular está com defeito, vem da máquina para?
Solução
Aqui, você tem um experimento que é realizado em duas partes; Na primeira parte, os eventos ocorrem:
Para: telefone celular feito pela máquina A.
B: telefone celular feito pela máquina B.
Como a máquina A produz 54% dos telefones celulares e o restante é produzido pela máquina B, a máquina B precisa produzir 46% dos telefones celulares. As chances desses eventos são dadas, a saber:
P (a) = 0,54.
P (b) = 0,46.
Os eventos da segunda parte do experimento são:
D: telefone celular defeituoso.
E: célula não definitiva.
Conforme declarado na declaração, as probabilidades desses eventos dependem do resultado obtido na primeira parte:
P (d | a) = 0,2.
P (D | B) = 0,5.
Usando esses valores, você também pode determinar as probabilidades dos acessórios desses eventos, ou seja:
P (e | a) = 1 - p (d | a)
= 1 - 0,2
= 0,8
e
P (e | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Agora, o evento D pode ser escrito da seguinte maneira:
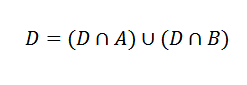 Esses eventos são mutuamente exclusivos.
Esses eventos são mutuamente exclusivos.
Usando o teorema da multiplicação para probabilidade condicional é:
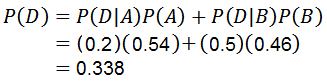
Com o qual a primeira pergunta é respondida.
Agora só precisamos calcular P (a | d), para o qual o teorema de Bayes é aplicado:
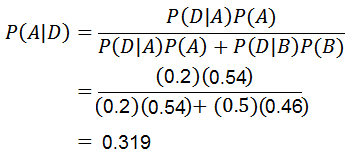
Graças ao teorema de Bayes, pode -se afirmar que a probabilidade de que um telefone celular tenha sido feito pela máquina A, sabendo que o telefone celular está com defeito, é 0.319.
Pode atendê -lo: icosagonoExercício 2
Três caixas contêm bolas pretas e pretas. A composição de cada um deles é a seguinte: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
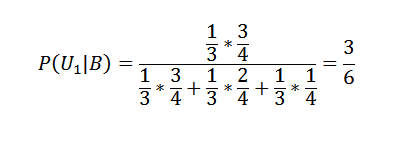
Um escolhido aleatoriamente uma das caixas e uma bola aleatória é extraída dela, que acaba sendo branca. Qual é a caixa com maior probabilidade de ter sido escolhida?
Solução
Através de U1, U2 e U3, também representaremos a caixa escolhida.
Esses eventos constituem uma partição de S e é verificado que p (u1) = p (u2) = p (u3) = 1/3 Como a escolha da caixa é aleatória.
Se b = a bola extraída for branca, teremos p (b | u1) = 3/4, p (b | u2) = 2/4, p (b | u3) = 1/4 .
O que queremos obter é a probabilidade de a bola ter sido retirada da caixa da IU, sabendo que essa bola era branca, isto é, P (Ui | B), e ver qual dos três valores foi o mais alto para saber qual de qual caixa tem maior probabilidade de extração da bola branca.
Aplicando o teorema de Bayes ao primeiro das caixas:
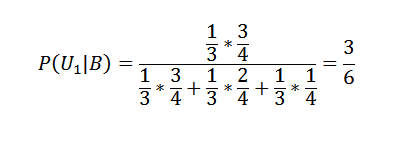
E para os outros dois:
P (u2 | b) = 2/6 e p (u3 | b) = 1/6.
Então, o primeiro das caixas é o que tem uma maior probabilidade de ter sido escolhido para a extração da bola branca.