Teoria das características dos conjuntos, elementos, exemplos, exercícios

O teoria de conjuntos É um ramo da lógica-matemática responsável pelo estudo das relações entre entidades chamadas conjuntos. Os conjuntos são caracterizados por ser coleções de objetos da mesma natureza. Esses objetos são os elementos do conjunto e podem ser: números, letras, figuras geométricas, palavras que representam objetos, os próprios objetos e outros.

Era Georg Cantor, no final do século XIX, quem propôs o conjunto de conjuntos. Enquanto outros matemáticos notáveis ​​no século XX fizeram sua formalização: Gottlob Frege, Ernst Zermelo, Bertrand Russell, Adolf Fraenkel, entre outros.

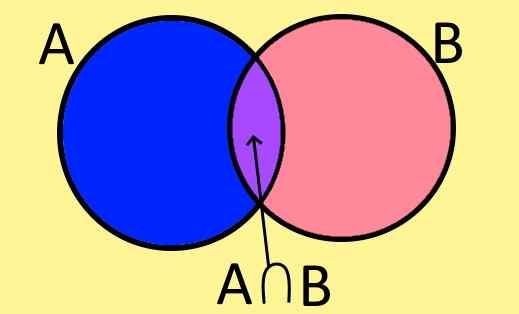
figura 1. Diagrama de Venn dos conjuntos A, B e seu cruzamento A⋂ B. (Elaboração própria).

Os diagramas de Venn são a maneira gráfica de representar um conjunto e consiste em uma figura plana fechada na qual os elementos do conjunto são.

Por exemplo, a Figura 1 mostra dois conjuntos A e B, que têm elementos em comum, os elementos comuns a A e B. Estes formam um novo conjunto chamado conjunto de interseção de A e B, que é escrito simbolicamente como segue:

A ∩ B

[TOC]

Caracteristicas

O conjunto é um conceito primitivo, como é na geometria o conceito de ponto, reto ou plano. Não há melhor maneira de expressar o conceito do que apontar exemplos: 

O conjunto e formado pelas cores da bandeira da Espanha. Essa maneira de expressar o conjunto é chamada pela compreensão. O mesmo conjunto e escrito por extensão é:

E = vermelho, amarelo

Nesse caso, vermelho e amarelo são elementos do conjunto e. Deve -se notar que os elementos estão listados entre as chaves e não são repetidos. No caso da bandeira espanhola, existem três faixas de cores (vermelho, amarelo, vermelho) duas das quais são repetidas, mas os elementos não são repetidos quando o conjunto é expresso.

Suponha que o Set V formado pelas três primeiras cartas vocais:

V = a, e, i

O poder de V, que é indicado por P (v) é o conjunto de todos os conjuntos que podem ser formados com os elementos de V:

P (v) = a, e, i, a, e, a, i, e, i, a, e, i

Tipos de conjuntos

Conjunto finito

É um conjunto no qual seus elementos são numerosos. Exemplos de conjuntos finitos são as letras do alfabeto espanhol, as vogais do espanhol, os planetas do sistema solar, entre outros. O número de elementos de um conjunto finito é chamado de cardinalidade.

Conjunto infinito

Ensemble Infinito, todo mundo que o número de seus elementos é incontestável, pois, independentemente do tamanho do número de seus elementos, é sempre possível encontrar mais elementos.

Um exemplo de conjunto infinito é o conjunto de números naturais n, que é extensivamente expresso da seguinte maneira:

Pode servir a você: coplanares pontos: equação, exemplo e exercícios resolvidos

N = 1, 2, 3, 4, 5, .. . é claramente um conjunto infinito, pois não importa o tamanho de um número natural, o curso seguinte sempre pode encontrar em um processo sem fim. Claramente a cardinalidade de um conjunto infinito é ∞.

Conjunto vazio

É o conjunto que não contém nenhum elemento. O conjunto vazio V é indicado por Ø ou por meio de um par de chaves sem elementos internos:

V = = Ø.

O conjunto vazio é único, portanto, deve ser incorreto dizer "um conjunto vazio", o formulário correto é dizer "o conjunto vazio".

Entre as propriedades do conjunto vazio, é que ele é subconjunto de qualquer conjunto:

Ø ⊂ a

Além disso, se um conjunto for subconjunto do conjunto vazio, esse conjunto será necessariamente o vazio:

A ⊂ Ø ⇔ a = Ø

Conjunto unitário

É chamado de conjunto unitário de qualquer conjunto que contenha um único elemento. Por exemplo, o conjunto de satélites naturais da terra é um conjunto de unidades, cujo único elemento é a lua. Definir B de números inteiros menores que 2 e maior que zero apenas o elemento 1, portanto, é um conjunto de unidades.

Conjunto binário

Um conjunto é binário se tiver apenas dois elementos. Por exemplo, defina x, de modo que x é um número real de x^2 = 2 = 2. Este conjunto por extensão é escrito assim:

X = -√2, +√2

Conjunto universal

O conjunto universal é um conjunto que contém outros conjuntos do mesmo tipo ou natureza. Por exemplo, o conjunto universal de números naturais é o conjunto de números reais. Mas números reais também são universais de números inteiros e números racionais.

Itens essenciais

- Relacionamentos entre conjuntos

Nos conjuntos, você pode estabelecer vários tipos de relacionamento entre eles e seus elementos. Se dois conjuntos A e B têm exatamente os mesmos elementos, entre eles, um relacionamento igual é indicado da seguinte maneira:

PARA = B

Se todos os elementos de um conjunto para pertencer a um conjunto B, mas não todos os elementos de B pertencem a A, então entre eles há um relacionamento de inclusão que é indicado da seguinte maneira:

A ⊂ b, mas b ⊄ a

A expressão anterior diz: A é subconjunto de B, mas B não é subconjunto de um.

Para indicar que alguns ou alguns elementos pertencem a um conjunto é usado o símbolo de pertencer ∈, por exemplo, para dizer que o elemento ou os elementos pertencem ao conjunto A é escrito simbolicamente como segue:

x ∈ A

Sim, um elemento e não pertence ao conjunto para esse relacionamento é escrito assim:

e ∉ a

A relação pertencente é dada entre os elementos de um conjunto e o conjunto, com a única exceção do conjunto de energia, sendo o conjunto a coleção ou conjunto de todos os conjuntos possíveis que podem ser formados com os elementos do referido conjunto.

Pode atendê -lo: fatorização

Suponha v = a, e, i, seu poder é p (v) = a, e, i, a, e, a, i, e, i, a, e, i, nesse caso o conjunto V se torna um elemento do conjunto p (v) e pode ser escrito:

V ∈ P (v)

- Propriedades de inclusão

A primeira propriedade da inclusão estabelece que todo conjunto está contido em si, ou em outras palavras, que é subconjunto de si mesmo:

A ⊂ a

A outra propriedade da inclusão é a transitividade: se A for subconjunto de B e B, por sua vez, é subconjunto de C, então a é subconjunto de C. Símbolo a relação de transitividade é escrita assim:

(A ⊂ b) ^ (b ⊂ c) => a ⊂ c

Abaixo está o diagrama de Venn correspondente à transitividade da inclusão:

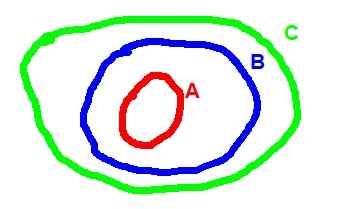Figura 2. (A ⊂ b) ^ (b ⊂ c) => a ⊂ c

- Operações entre conjuntos

Interseção

A interseção é uma operação entre dois conjuntos que resulta em um novo conjunto pertencente ao mesmo conjunto universal dos dois primeiros. Nesse sentido, é uma operação fechada.

Simbolicamente, a operação de interseção é formulada da seguinte forma:

A⋂b = x / x∈A ^ x∈B

Um exemplo é o seguinte: Defina uma das letras da palavra "elementos" e o conjunto B das letras da palavra "repetido", a interseção entre A e B é escrita assim:

A⋂b = e, l, m, n, t, s ⋂ r, e, p, t, i, d, o, s = e, t, s . O conjunto universal de A, de B e também de A⋂b é o conjunto das letras do alfabeto espanhol.

União

A união de dois conjuntos é o conjunto formado pelos elementos comuns aos dois conjuntos e aos elementos não comuns dos dois conjuntos. A operação da união entre os conjuntos é expressa simbolicamente da seguinte forma:

A∪b = x/x∈A v x∈B

Diferença

A operação do conjunto pelo menos o conjunto é indicado por A-B. A-B é um novo conjunto formado por todos os elementos que estão em A e que não pertencem a B. O símbolo está escrito assim:

A - b = x/ x ∈ A ^ x ∉ b

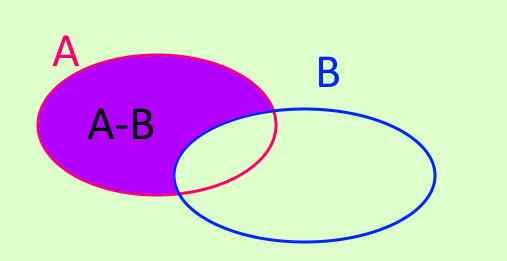Figura 3. A - b = x/ x ∈ A ^ x ∉ b

Diferença simétrica

A diferença simétrica é uma operação entre dois conjuntos em que o conjunto resultante é composto pelos elementos não comuns aos dois conjuntos. A diferença simétrica simbolicamente é representada da seguinte maneira:

A⊕b = x/ x∈ (a-b) ^ x∈ (b-a)

Exemplos

Exemplo 1

O diagrama de Venn é uma maneira gráfica de representar os conjuntos. Por exemplo, o conjunto C das letras do conjunto de palavras é representado da seguinte forma:

Exemplo 2

É mostrado abaixo através dos diagramas de Venn que, o conjunto de vogais na palavra "conjunto", é um subconjunto do conjunto das letras da palavra "conjunto".

Pode servir a você: amostragem de cotas: método, vantagens, desvantagens, exemplos

Exemplo 3

O conjunto Ñ Das cartas do alfabeto espanhol, é um conjunto finito, este conjunto por extensão é escrito assim:

Ñ = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z e seu A cardinalidade é 27.

Exemplo 4

O conjunto V Das vogais em espanhol, é um subconjunto do conjunto ñ:

V ⊂ Ñ Portanto, é um conjunto finito.

O conjunto finito V A maneira estendida é escrita assim: V = a, e, i, o, u e sua cardinalidade é 5.

Exemplo 5

Dados os conjuntos A = 2, 4, 6, 8 e ​​B = 1, 2, 4, 7, 9 Determine A-B e B-A. 

A - B são os elementos dos quais eles não estão em B:

A - b = 6, 8

B - A são os elementos de B que não estão em A:

B - a = 1, 7, 9

Exercícios resolvidos

Exercício 1

Escreva simbólico e também, por extensão, a pétala P de números naturais ainda inferiores a 10.

Solução: P = x∈ N / x < 10 ^ x mod 2 = 0

P = 2, 4, 6, 8

Exercício 2

Suponha o todo ao formado pelos números naturais que são fatores de 210 e o conjunto B formado pelos números naturais primos inferiores a 9. Determine os dois conjuntos por extensão e estabeleça qual relacionamento há entre os dois conjuntos.

Solução: Para determinar os elementos do conjunto A, você deve começar encontrando os fatores do número natural 210:

210 = 2 * 3 * 5 * 7

Em seguida, o conjunto A está escrito:

A = 2, 3, 5, 7

Continuamos a considerar o conjunto B, que é os primos menores que 9. O 1 não é primo porque não atende à definição de primo: "Um número é primo se e somente se tiver exatamente dois divisores o 1 e o próprio número". O 2 é par e, ao mesmo tempo, é primo porque atende à definição de primo, os outros primos menores que 9 são 3, 5 e 7. Então esse conjunto B é:

B = 2, 3, 5, 7

Portanto, os dois conjuntos são os mesmos: um = B.

Exercício 3

Determine o conjunto cujos elementos x são diferentes de x.

Solução: C = x / x ≠ x

Como qualquer elemento, número ou objeto é igual a si mesmo, o conjunto C não pode ser diferente do conjunto vazio:

C = Ø

Exercício 4

Seja o conjunto de N de números naturais e z o conjunto de números inteiros. Determinar n ⋂ z y n ∪ z.

Solução: 

N ⋂ z = x ∈ Z / x ≤ 0 = (-∞, 0]

N ∪ z = z porque n ⊂ z.

Referências

1. Garo, m. (2014). Matemática: Equações quadráticas: Como resolver uma equação quadrática. Marilù Garo.
2. Haeussler, e. F., E Paul, r. S. (2003). Matemática para Administração e Economia. Pearson Education.
3. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matemática 1 de setembro. Limite.
4. Precioso, c. T. (2005). Curso de Matemática 3O. Editorial Progreso.
5. Matemática 10 (2018). "Exemplos de conjuntos finitos". Recuperado de: Mathematics10.líquido
6. Wikipedia. Teoria de conjuntos. Recuperado de: é.Wikipedia.com