Soma da história, fórmulas e propriedades de Riemann, exercícios

O Riemann Sum É o nome que recebe o cálculo aproximado de uma integral definida, por meio de uma soma discreta com um número de termos finitos. Uma aplicação comum é a abordagem da área de funções em um gráfico.

Foi o matemático alemão Georg Friedrich Bernhard Riemann (1826-1866) que ofereceu pela primeira vez uma definição rigorosa da integral de uma função em um determinado intervalo. Ele anunciou em um artigo publicado em 1854. 

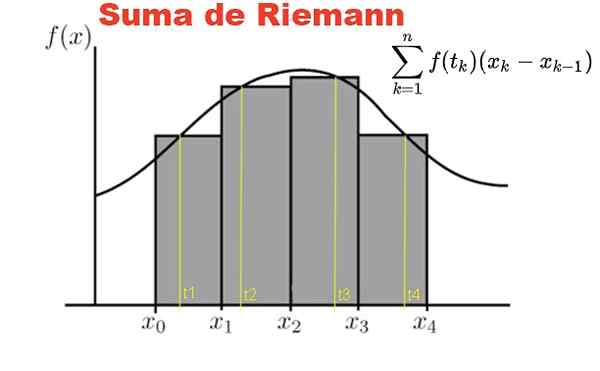
figura 1. A soma de Riemann é definida em uma função f e uma partição no intervalo [x0, x1]. Fonte: Fanny Zapata.

A soma de Riemann é definida em uma função y = f (x), com X pertencente ao intervalo fechado [a, b]. Nesse intervalo, é feita uma partição p de n elementos:

P = x₀= a, x₁, x₂,…, X_n= b

Isso significa que o intervalo é dividido da seguinte maneira:

 Aqui t_k está entre x_K-1 e x_k:

x_K-1 ≤ t_k ≤ x_k

A Figura 1 mostra a soma de Riemann da função f no intervalo [x₀, x₄] Em uma partição de quatro subintervais, retângulos cinza.

A soma representa a área total dos retângulos e o resultado dessa soma é numericamente abordagens para a área sob a curva f, entre as abcissas x = x₀ y x = x₄.

Obviamente, a abordagem da área sob a curva melhora muito na medida em que o número n de partições é maior.  Dessa maneira, a soma converge para a área sob a curva, quando o número n Partições tendem ao infinito.

[TOC]

Fórmulas e propriedades

Função Soma de F (x) de Riemann na Partição:

Pode servir a você: Rhomboid: Características, como tirar o perímetro e a área

P = x₀= a, x₁, x₂,…, X_n= b

Definido no intervalo [a, b], é dado por:

S (p, f) = ∑_{K = 1}ⁿ f (t_k) (x_k - x_K-1) 

Onde t_k É um valor no intervalo [x_k, x_K-1]. Na soma de Riemann, intervalos regulares de larguras são geralmente usados ​​Δx = (b - a)/n, onde A e B são os valores mínimo e máximo da abscissa, enquanto n é o número de subdivisões.

Nesse caso o Soma certa de Riemann é:

Sd (f, n) = [f (a+Δx)+f (a+2Δx)+…+f (a+(n-1) Δx)+f (b)]*Δx

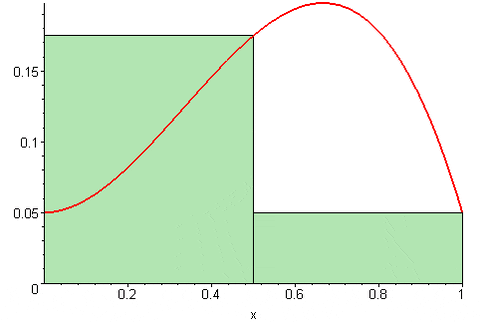Figura 2. Soma certa de Riemann. Fonte: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0)].

Enquanto o Soma esquerda de Riemann É expresso como:

Sim (f, n) = [f (a)+f (a+Δx)+…+f (a+(n-1) Δx)]*Δx

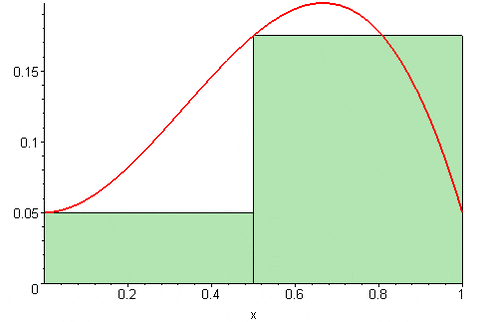Figura 3. Soma de Riemann saiu. Fonte: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Finalmente, o Soma central de Riemann é:

Sc (f, n) = [f (a+Δx/2)+f (a+3Δx/2)+…+f (b- Δx/2)]*Δx

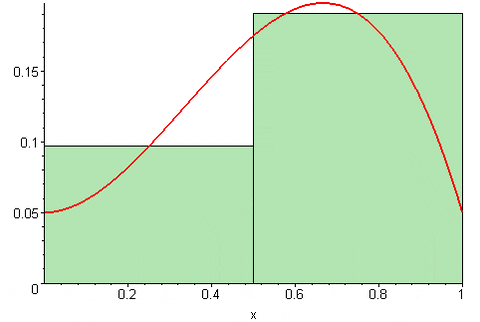Figura 4. Soma intermediária de Riemann. Fonte: Wikimedia Commons. 09Glasgow09 [CC BY-SA (https: // CreativeCommons.Org/licenças/BY-SA/3.0)]

Dependendo de onde o ponto t está localizado_k No intervalo [x_k, x_K-1] A soma de Riemann pode superestimar ou subestimar o valor exato da área sob a curva de função y = f (x) (x). Isto é, os retângulos podem se destacar da curva ou ficar um pouco abaixo disso.

A área sob a curva

A principal propriedade da soma de Riemann e da qual sua importância se torna, é que, se o número de subdivisões tende ao infinito, o resultado da soma converge para a integral definida da função:

A expressão anterior corresponde à definição de integral e aplica de Riemann, desde que a função f seja contínua e macia. Para funções mais particulares, existem outras definições da integral (integral de Stieldjes e integral de Lebesgue).

Pode servir a você: erro de estimativa padrão: como é calculado, exemplos, exercícios

Exercícios resolvidos

- Exercício 1

Calcule o valor da integral definida entre a = -2 a b = +2 da função:

f (x) = x²

Faça uso de uma soma de Riemann. Para fazer isso, encontre a soma para partições regulares do intervalo [a, b] e depois pegue o limite matemático para o caso de que o número de partições armazene para o infinito. 

Solução

Estas são as etapas a seguir:

-Primeiro, o intervalo de partição é definido como: 

Δx = (b - a)/n. 

-Então a soma de Riemann à direita correspondente à função f (x) é assim:

-Agora eles são substituídos a = -2 e b =+2, de modo que o intervalo ou a etapa Δx = 4/n. Ou seja, a soma de Riemann para a função f (x) = x² é:

-Então o binomial quadrado é desenvolvido: 

[-2 +(4i/n)]² = 4 - (16 i /n) + (4 /n)² Yo²

-E então é cuidadosamente substituído na soma:

-O próximo passo é separar os resumos e remover as quantidades constantes como um fator comum de cada soma. É necessário levar em consideração que o índice é i, portanto os números e os termos com n Eles são considerados constantes:

-Cada soma é avaliada, pois para cada um deles há expressões apropriadas. Por exemplo, o primeiro dos resumos da n:

O segundo é:

 E o terceiro é:

 -Substituindo os resultados dos resumos na soma de Riemann, finalmente é obtido:

S (f, n) = 16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²

-Finalmente você tem que calcular a integral é:

= lim_N➝∞ [16 - 64 (n+1)/2n+64 (n+1) (2n+1)/6n²] =

= 16 -(64/2) + (64/3) = 16/3 = 5,333

O leitor pode verificar se este é o resultado exato, que pode ser obtido resolvendo a integral indefinida e avaliando os limites de integração pela regra de Barrow.

Pode atendê -lo: como converter de km/h a m/s? Exercícios resolvidos

- Exercício 2

Determine aproximadamente a área sob a função: 

f (x) = (1/√ (2π) e^(-x2/2)

Entre x = -1 e x =+1, usando uma soma central de Riemann com 10 partições. Compare com o resultado exato e estimar a diferença percentual.

Solução

A etapa ou aumento entre dois valores discretos sucessivos é:

Δx = (1 - (-1)/10 = 0,2

Para que a partição P na qual os retângulos sejam definidos seja assim:

P = -1,0; -0,8; -0,6; -0,4; -0,2; 0,0; 0,2; 0,4; 0,6; 0,8; 1.0

Mas como você deseja é a soma central, a função f (x) será avaliada nos pontos médios dos subintervalos, ou seja, no conjunto:

T = -0.9; -0,7; -0,5; -0,3; -0,1; 0,1; 0,3; 0,5; 0,7; 0,9.

A soma de Riemann (central) é assim:

S = f (-0,9)*0,2 +f (-0,7)*0,2 +f (-0,5)*0,2 +… +f (0,7)*0,2 +f (0,9)*0,2

Como a função F é simétrica, é possível reduzir a soma a apenas 5 termos e o resultado é multiplicado por dois:

S = 2*0,2*f (0,1)+ f (0,3)+ f (0,5)+ f (0,7)+ f (0,9)

S = 2*0,2*0,397+ 0,381+ 0,352+ 0,312+ 0,266 = 0,683

A função dada neste exemplo não é outra senão o bem conhecido Gauss Bell (normalizado, com média igual a zero e desvio padrão um). Sabe-se que a área sob a curva no intervalo [-1,1] para esta função é 0,6827.

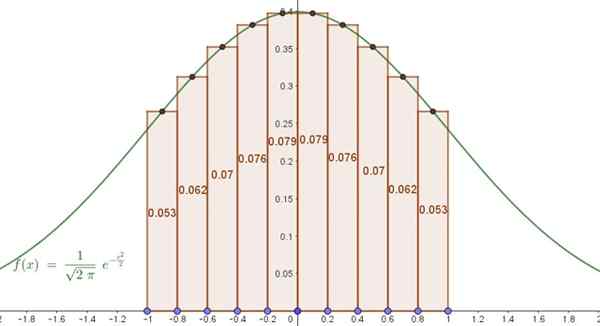Figura 5. Área sob um Bell Gauss aproximado por meio de uma soma de Riemann. Fonte: f. Zapata.

Isso significa que a solução aproximada com apenas 10 termos coincide com a solução exata até três decimais. O erro percentual entre a integral aproximada e o exato é de 0,07%.

Referências

1. Casteleiro, J. M., & Gómez-Alvarez, R. P. (2002). Cálculo abrangente (ilustrado ed.). Madri: editorial ESIC.
2. Unican. História do conceito de integral. Recuperado de: repositório.Unican.é
3. UIs. Riemann somas. Recuperado de: matemática.UIs.Edu.co
4. Wikipedia. Riemann Sum. Recuperado de: é.Wikipedia.com
5. Wikipedia. Integração de Riemann. Recuperado de: é.Wikipedia.com