Sucessão composta

Sucessão composta por quadrados amarelos e azuis. Fonte: f. Zapata

O que é uma sucessão composta?

A sucessão composta Consiste em uma sequência de elementos, criada a partir de duas (ou mais) sucessões diferentes e alternativas. Cada uma dessas sucessões tem uma regra específica, usada para encontrar seus respectivos elementos.

Os elementos não precisam ser numéricos, sendo capazes de ser números, símbolos ou letras, mas aqueles que são baseados em números são chamados sucessões aritméticas. A figura com a qual nosso artigo começa mostra uma sucessão composta de quadrados amarelos e azuis.

Nesta sucessão, começa a partir de um quadrado grande composto por 8 quadrados amarelos e um quadrado azul. Para obter o seguinte termo, um quadrado amarelo é adicionado à esquerda ou à direita da primeira e a terceira fila de quadrados. O espaço que resulta na linha central é preenchido com um quadrado azul.

Cada figura na sequência é chamada prazo. Se você deseja encontrar o quinto termo, deve adicionar um quadrado amarelo à direita da primeira e terceira fileiras, e um quadrado azul na segunda linha:

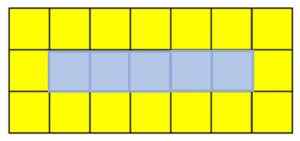Quinto mandato de uma sucessão de quadrados amarelos e azuis. Fonte: f. Zapata

Explicação

Nas sucessões compostas, os termos são obtidos alternando os termos de duas ou mais sucessões simples independentes. Para entender melhor a ideia, deve ser revisado os detalhes de uma simples sucessão.

Por exemplo, a seguinte sucessão simples consiste nos números naturais:

2, 4, 6, 8, 10, 12 ..

Os pontos suspeitos indicam que a sucessão tem termos infinitos.

Cada um dos termos é indicado por uma pequena carta e um número, como um subscrito. Este número indica a posição ou índice de cada termo. Na sucessão anterior, você pode escrever:

para₁ = 2; para₂ = 4; para₃ = 6; para₄ = 8 ..

É muito conveniente ter uma maneira de calcular qualquer termo desejado da sucessão, ou seja, sua regra particular. Com ela o Termo n-ésimo, qualquer Termo geral, denotado como um_n.

Pode atendê -lo: propriedades de igualdade

Continuando com o exemplo da sucessão de números uniformes, você pode estabelecer o caminho para calcular o termo n-ésimo, a partir do termo anterior:

para_n = a_N-1 + 2

Para onde_N-1 É o termo que precede_n.

Claro que seria melhor conhecer o termo geral sem depender de outros termos. Nesta sucessão, é fácil observar que qualquer termo está se multiplicando por 2 a posição que ocupa, dado o subscrito do termo. Dessa forma, está escrito:

para_n = 2n

Os gregos antigos já conheciam as sucessões de números pares e estranhos. A sucessão de números naturais estranhos, enquanto isso, pode ser escrito como:

1, 3, 5, 7, 9, 11 ..

E combinando a sucessão dos números pares com o do ímpar, a seguinte sucessão composta é:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..

Cujo resultado é o conjunto de números naturais.

Termos de uma sucessão composta

Pode ser divertido tentar encontrar o relacionamento que existe em uma sequência de números, para os quais deve ser cuidadosamente observado e tentar identificar se é uma sucessão composta.

A forma geral de uma sucessão composta por duas sucessões será:

para₁, b₁, para₂, b₂, para₃, b₃, para₄, b₄,..

Para onde₁, para₂, para₃, para₄,... são os termos da primeira sucessão e B₁, b₂, b₃, b₄,... aqueles do segundo. Eles são sempre intercalados, como é o caso neste exemplo:

7, 8, 14, 16, vinte e um, 24, 28, 32, 35..

Qual será o termo que se segue?

Para saber, conheça a sucessão em dois conjuntos de números alternativos, da seguinte forma:

• 7, 14, 21, 28, 35 ..
• 8, 16, 24, 32 ..

No primeiro desses conjuntos, os múltiplos de 7 aparecem:

para₁ = 7 × 1 = 7; para₂ = 7 × 2 = 14; para₃ = 7 × 3 = 21; para₄ = 7 × 4 = 28; para₅ = 7 × 5 = 35

O termo geral desta sucessão é:

para_n = 7n

E no segundo, são os múltiplos de 8:

b₁ = 8 × 1 = 8; b₂ = 8 × 2 = 16; b₃ = 8 × 3 = 24; b₄ = 8 × 4 = 32

Portanto, seu termo geral é:

Pode atendê -lo: função variável real e sua representação gráfica

b_n = 8n

Voltando à sucessão composta original, o 35 pertence à primeira sequência, cujos termos são para₁, para₂, para₃, para₄ … 35 é o quinto termo, então o termo a seguir deve ser B₅, que é facilmente obtido da regra para encontrar o termo geral:

b₅ = 8 × 5 = 40

E está escrito:

7, 8, 14, 16, vinte e um, 24, 28, 32, 35, 40 ..

Exemplos de sucessões compostas

Exemplo 1

Você pode criar uma sucessão composta com figuras geométricas, como o quadrado e o círculo, organizando -os como mostrado abaixo:

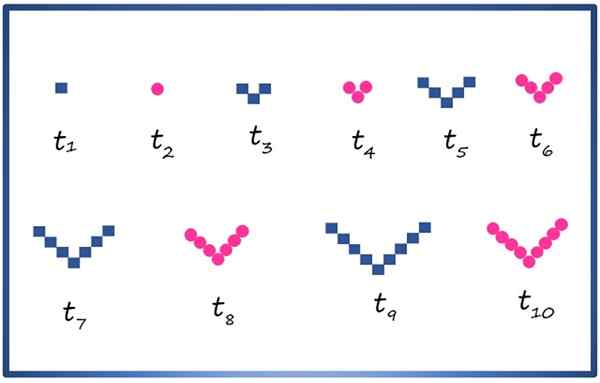Os 10 primeiros termos de uma sucessão composta com os elementos e círculos geométricos quadrados. Fonte: f. Zapata

Cada termo é indicado por T₁, t₂, t₃, t₄ …, Os termos do índice de parque consistem em círculos e os de Índice ímpar, quadrados. Observando cuidadosamente a sequência, é possível saber, por exemplo, que o termo t_onze, Isso não aparece na imagem, consiste em 11 quadrados com a disposição em V.

Exemplo 2

A seguinte sucessão composta consiste em símbolos, neste caso, as letras r e s:

R ss rr sss rrr sss rrrr ssss rrrr ssssss ..

Cada novo termo é construído adicionando uma letra ao anterior. Os quatro primeiros termos da sequência mostrados são:

t₁= R ; t₂= H.H ; t₃= Rr ; t₄= SSS ..

E o próximo termo que apareceria após os termos mostrados é:

t_onze= Rrrrrr

Exemplo 3

Os exemplos anteriores mostraram sucessões ascendentes, nas quais cada valor aumenta, de alguma forma, com relação ao anterior. Mas nem sempre precisa ser dessa maneira, uma vez que as sucessões podem descer, ou seja, elas têm um padrão de diminuição.

E sucessões ascendentes podem ser combinadas com sucessões descendentes.

A seguinte sucessão numérica é composta:

4, 36, 7, 35, 10, ___, ___, 33, 16, ___, ___, ..

Pode ser separado em duas sucessões:

• 4, 7, 10, ___, 16, ___, ..
• 36, 35, ___, 33, ___, ..

Quais são os valores que devem ser colocados nos espaços em branco?

Observando cuidadosamente a primeira sucessão, cada termo é obtido adicionando 3 ao termo anterior. É, portanto, uma sucessão ascendente:

Pode atendê -lo: deslocamento angular

7 = 4 + 3

10 = 7 + 3

Portanto, no primeiro espaço em branco, você deve colocar:

10 + 3 = 13

Depois disso, o período seguinte é, com efeito:

16 = 13 + 3

E o que vai no segundo espaço em branco é:

16 + 3 = 19

A segunda sucessão está descendo e é muito fácil encontrar os termos ausentes, pois é observado que cada termo é obtido subtraindo 1 do termo anterior, portanto:

36, 35, 3. 4, 33, 32..

Finalmente, você pode escrever:

4, 36, 7, 35, 10, 3. 4, 13, 33, 16, 32, 19,..

Exercícios resolvidos

Exercício 1

Na sucessão, composta pelo Exemplo 3 na seção anterior:

a) 29 pertence à referida sucessão?

b) Escreva mais 10 termos desta sucessão

Responda para

Sim, ele pertence, já que a segunda sucessão está descendo e seus termos são obtidos subtraindo 1 do termo anterior. Dessa forma, acaba chegando a 29.

Resposta b

4, 36, 7, 35, 10, 34, 13, 33, 16, 32, 19, 31, 22, 25, 29, 28, 31, 27, 34, ..

Observe que alguns termos são repetidos.

Exercício 2

Encontre os termos ausentes na seguinte sucessão composta:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, ..

Responder

Os termos ímpares são escritos para obter a primeira sucessão:

100, 115, 130, 145, 160, ..

Observa -se que, para encontrar cada termo, você deve adicionar 15 ao termo anterior, portanto, o termo a seguir em 160 é 175.

A segunda sucessão consiste em:

500, 480, 460, 440, 420, ..

Cada termo difere do anterior a 20, sendo a sucessão descendo, portanto, o termo seguido em 420 é 400.

Com essas informações, mais dois termos são adicionados à sucessão composta original, como esta:

100, 500, 115, 480, 130, 460, 145, 440, 160, 420, 175, 400, ..

Referências

1. Larson, r. (2012). Pré -cálculo. 8º. Edição. Cengage Learning.
2. Stewart, J. (2007). Preccculment: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
3. Sucessões compostas. Recuperado de: mídia.EducacionCampeche.GO.mx.
4. Sucessões numéricas. Recuperado de: Matemathweb.com.
5. Sucessões. Progressões aritméticas e geométricas. Recuperado de: MacMillaNeDucation.é.