Propriedades, exemplos e exercícios de simetria central

Dois pontos A e 'têm Simetria central em relação a um ponto ou quando o segmento AA 'passa por ele e também é o ponto médio de AA'. Ao ponto ou é chamado Centro de Simetria.

O simétrico central de um triângulo ABC em relação a um ponto ou, é outro triângulo A'b'c 'que possui as seguintes características:

-Segmentos homólogos são iguais 

-Seus ângulos correspondentes têm a mesma medida.

figura 1. Triângulo ABC e seu simétrico A'b'c '. Fonte: f. Zapata.

Na Figura 1, um triângulo ABC (vermelho) e seu A'B'c 'Central (verde), com relação ao centro de simetria ou. 

Nesta mesma figura, um observador atento perceberia que o mesmo resultado é obtido aplicando uma rotação original do triângulo, desde que seja 180º e focada em ou.

Portanto, uma simetria central é equivalente a uma virada de 180º em relação ao centro da simetria.

[TOC]

Propriedades da simetria central

Uma simetria central tem as seguintes propriedades:

-O centro de simetria é o ponto médio do segmento que se junta a um ponto com seu simétrico.

-Um ponto simétrico de outro que está localizado no centro de simetria, coincide com o centro de simetria.

-O simétrico central de um triângulo é um triângulo congruente (igual.

-A imagem por simetria central de uma circunferência é outra circunferência de raio igual.

-Um círculo tem simetria central em relação ao seu próprio centro.

Figura 2. Design com simetria central. Fonte: Pixabay.

-A elipse tem simetria central em relação ao seu centro.

-Um segmento tem simetria central em relação ao seu ponto médio.

-O triângulo equilátero não tem simetria central em relação ao seu centro, porque seu simétrico, embora congruente ao primeiro, dá um triângulo equilátero virado.

Pode atendê -lo: y = 3sen (4x) Período de função

-Os quadrados têm simetria central em relação ao seu centro.

-Um Pentágono carece de simetria central em relação ao seu centro.

-Os polígonos regulares têm simetria central quando têm vários lados de torque.

Exemplos

Os critérios de simetria têm muitas aplicações em ciências e engenharia. A simetria central está presente na natureza, por exemplo, cristais de gelo e teias de aranha têm esse tipo de simetria.

Além disso, muitos problemas são facilmente resolvidos quando a existência de simetria central e outros tipos de simetria é usada. Portanto, é conveniente identificar rapidamente quando ocorre.

Figura 3. Cristais de gelo têm simetria central. Fonte: Pixabay.

Exemplo 1

Dado um ponto P de coordenadas (a, b), você precisa encontrar as coordenadas de seu p 'simétrico em relação à origem ou coordenadas (0, 0).

A primeira coisa é construir o P 'P', para o qual é desenhado uma linha que passa pela origem ou e pelo ponto P. A equação desta linha é y = (b/a) x.

Agora vamos chamar (a ', b') as coordenadas do ponto simétrico P '. Ponto p. Além disso, a distância do OP deve ser igual à OP ', que escreve analiticamente como este:

√ (a² + b²) = √ (a '² + B '² )

O seguinte é substituir B '= [(B/A).A '] na expressão anterior e quadrado em ambos os lados da igualdade para eliminar a raiz quadrada: (a² + b²) = [a '² + (b²/para²).para'²]

Ao extrair fator comum e simplificar, é alcançado para '² = a². Esta equação tem duas soluções reais: a '= +a ou a' = -a. 

Para obter B ', usamos novamente b' = (b/a) a '. Se a solução positiva de A for substituída, é alcançado que B '= B. E quando a solução negativa é substituída, então b '= -b. 

Pode atendê -lo: quais são os 7 elementos da circunferência?

A solução positiva fornece para p 'o mesmo ponto P, então é descartado. A solução negativa definitivamente oferece as coordenadas do ponto simétrico:

P ': (-a, -b)

Exemplo 2

É necessário demonstrar que um segmento AB e seu A'B central simétrico têm o mesmo comprimento.

Começando com as coordenadas do ponto A, que são (ax, ay) e as do ponto B: (bx, por), o comprimento do AB é dado por:

D (ab) = √ ((bx - ax)² + (Por - ay)² )

Por analogia, o segmento simétrico A'B 'terá duração dada por:

d (a'b ') = √ ((bx' - ax ')² + (Por ' - ay')² )

As coordenadas do ponto simétrico a 'são ax' = -ax e ay '= -ay. Da mesma forma, os de B 'são Bx' = -bx e por '= -by. Se essas coordenadas forem substituídas na equação da distância d (a'b '), você tem:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) que é equivalente a:

 √ ((bx - machado)² + (Por - ay)²) = D (AB)

Sendo demonstrado que ambos os segmentos têm o mesmo comprimento.

Exercícios resolvidos

- Exercício 1

Demonstrar de uma maneira analítica que o central simétrico ou um círculo de raio r e centro ou, é a mesma circunferência original.

Solução

A equação de um raio r e círculo central (0,0) é:

x² + e² = R² (Equação de circunferência C)

Se em cada ponto P da circunferência e coordenadas (x, y), sua coordenada simétrica é encontrada, a equação da circunferência simétrica é:

x '² + e'² = R² (Equação de circunferência simétrica C ')

Agora, nos referimos ao resultado do Exemplo 1, que conclui que as coordenadas de um ponto P ', simétricas para p e coordenadas (a, b), são (-a, -b). 

Mas neste exercício, o ponto P tem coordenadas (x, y), então seu p 'simétrico terá coordenadas x' = -x e y '= -y. Substituir isso na equação de circunferência simétrica é:

Pode servir a você: Rhomboid: Características, como tirar o perímetro e a área

(-X)² + (-e)² = R²

Que é equivalente a: x²+ e² = R², Concluindo que a simétrica central de um círculo em relação ao seu centro é a própria circunferência.

- Exercício 2

Demonstrar de uma maneira geométrica que a simetria central preserva os ângulos.

Solução

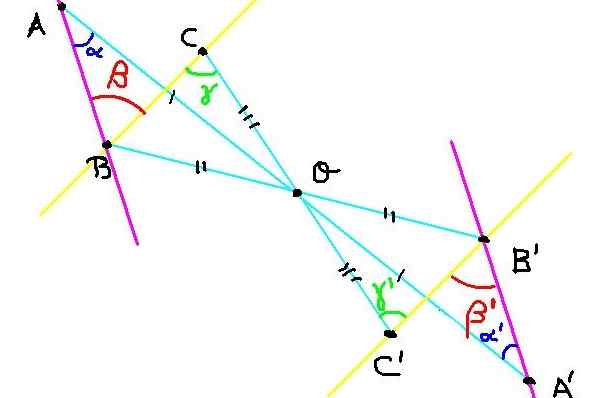Figura 4. Construção de pontos simétricos para o Exercício 2. Fonte: f. Zapata.

Existem três pontos A, B e C no avião. Seu simétrico a ', b' e c 'são construídos em relação ao centro de simetria ou, como mostrado na Figura 4. 

Agora devemos demonstrar que o ângulo ∡ABC = β tem a mesma medida que o ângulo ∡a'b'c '= β' '.

Como C e C 'são simétricos, então oc = oc'. Da mesma forma ob = ob 'y oa = oa'. Por outro lado, o ângulo ∡boc = ∡b'oc 'por ser oposto ao vértice.

Então os triângulos Boc e B'oc 'são congruentes por terem um ângulo igual entre dois lados iguais.

Porque o BOC é congruente para B'oc 'então os ângulos  γ e γ ' são iguais. Mas esses ângulos, além de cumprir γ = γ ' Eles são alternados internos entre as linhas BC e B'C, o que implica que a linha BC é paralela ao B'C '.

Da mesma forma, Baa é congruente com o que é seguido que α = α ' . Mas  α e α ' São ângulos alternativos internos entre as linhas BA e B'A, das quais conclui -se que a linha BA é paralela a B'a '.

Como o ângulo ∡ABC = β tem seus lados paralelos com o ângulo ∡a'b'c '= β' e também ambos são agudos, conclui -se que:

∡abc = ∡a'b'c '= β = β' '

Demonstrando dessa maneira que a simetria central mantém a medida dos ângulos.

Referências

1. Baldor, J. PARA. 1973.Geometria plana e espacial. Cultural da América Central. 
2. Leis e fórmulas matemáticas. Sistemas de medição de ângulo. Recuperado de: IngeMecanica.com.
3. Wentworth, G. Geometria do Planeta. Recuperado de: Gutenberg.org.
4. Wikipedia. Simetria central. Recuperado de: é.Wikipedia.com
5. Wikipedia. Transportador. Recuperado de: é.Wikipedia.com
6. Zapata f. Ângulos conjugados internos e externos. Recuperado de: Lifer.com