Ângulos complementares que e como são calculados, exemplos, exercícios

Dois ou mais ângulos são ângulos complementares Se a soma de suas medidas corresponde à de um ângulo reto. Como se sabe, a medida de um ângulo reto em graus é de 90º e em Radianes é π/2.

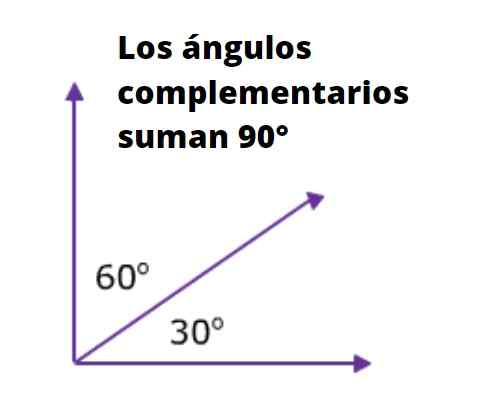
Por exemplo, os dois ângulos adjacentes à hipotenusa de um triângulo retângulo são complementares um ao outro, uma vez que a soma de suas medidas é 90º. A figura a seguir é muito ilustrativa sobre isso:

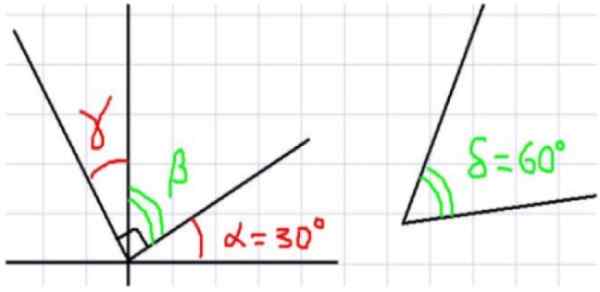figura 1. À esquerda, vários ângulos com um vértice comum. À direita um ângulo de 60º que complementa o ângulo α (alfa). Fonte: f. Zapata.

A Figura 1 mostra um total de quatro ângulos. α e β são complementares, pois são adjacente e sua soma completa um ângulo reto. Da mesma forma, β é complementar a γ, onde se segue que γ e α são de igual medida.

Agora, como a soma de α e δ é igual a 90 graus, pode -se dizer que α e δ são complementares. Além disso, como β e δ têm o mesmo α complementar, pode -se dizer que β e δ têm a mesma medida.

 [TOC]

Exemplos de ângulos complementares

Nos exemplos a seguir, é solicitado que encontre os ângulos desconhecidos, indicados com interrogatório na Figura 2.

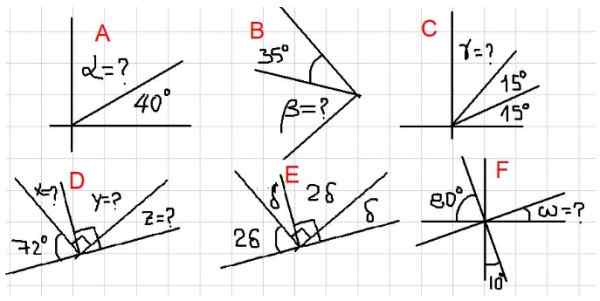Figura 2. Vários exemplos de ângulos complementares. Fonte: f. Zapata.

- Exemplos A, B e C

Os exemplos a seguir estão em ordem de complexidade.

Exemplo a

Na figura superior, temos que os ângulos adjacentes α e 40º somam um ângulo reto. Isto é α + 40º = 90º, portanto α = 90º- 40º = 50º.

Exemplo b

Como β é complementar com o ângulo de 35º, depois β = 90º - 35º = 55º.

Pode servir a você: Orthoedro: fórmulas, área, volume, diagonal, exemplos

Exemplo c

Na Figura 2c, a soma de γ + 15º + 15º = 90º. Ou seja, γ é complementar ao ângulo 30 = 15º + 15º. De maneira que:

γ = 90º- 30º = 60º

- Exemplos D, E e F

Nesses exemplos, há mais ângulos envolvidos. Para encontrar as incógnitas, o leitor deve aplicar o conceito de ângulo complementar quantas vezes for necessário.

Exemplo d

Como x é complementar com 72º, segue -se que x = 90º - 72º = 18º. Além disso e é complementar com x, então y = 90º - 18º = 72º.

Finalmente z é complementar a e. De tudo isso, segue -se que:

Z = 90º - 72º = 18º

Exemplo e

Os ângulos δ e 2Δ são complementares, portanto Δ + 2Δ = 90º.

Isto é 3Δ = 90º, o que implica que δ = 90º / 3 = 30º.

Exemplo f

Se chamarmos o ângulo entre ω e o de 10, ele deve ser suplementado a eles, porque é observado que sua soma completa é um ângulo reto. Onde se segue que u = 80º. Como u é complementar com ω, então ω = 10º.

Exercícios

Três exercícios são propostos abaixo. Em todos eles, o valor dos ângulos A e B deve ser encontrado em graus, para que os relacionamentos mostrados na Figura 3 sejam atendidos.

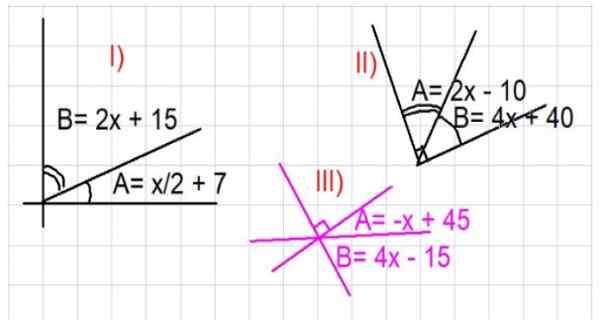Figura 3. Ilustrações para exercícios de ângulos complementares. Fonte: f. Zapata.

- Exercício 1

Determine os valores dos ângulos A e B da Parte I) da Figura 3.

Solução

A partir da figura mostrada, é visto que A e B são complementares, portanto A + B = 90º. A expressão de A e B é substituída em função de x dada na Parte I):

Pode servir a você: Rádio de Convergência: Definição, Exemplos e Exercícios resolvidos

(x/2 + 7) + (2x + 15) = 90

Em seguida, os termos são agrupados adequadamente e uma equação linear simples é obtida:

(5x/2) + 22 = 90

Subtraindo 22 em ambos os membros são:

5x/2 = 90 -22 = 68

E finalmente o valor de x é liberado:

x = 2*68/5 = 136/5

Agora o ângulo é encontrado substituindo o valor de x:

A = (136/5)/2 +7 = 103/5 = 20,6 º.

Enquanto o ângulo B é:

B = 2*136/5 + 15 = 347/5º = 69,4º .

- Exercício 2

Encontre os valores dos ângulos A e B da imagem II, Figura 3.

Solução

Novamente, como A e B são ângulos complementares, você precisa: a + b = 90º. Substituir a expressão de A e B em função de x dada na Parte II) da Figura 3 é:

(2x - 10) + (4x +40) = 90

Os termos semelhantes são agrupados para obter a equação:

6 x + 30 = 90

Dividindo os dois membros entre 6 é obtido:

x + 5 = 15

Onde se segue que x = 10º.

Portanto:

A = 2*10 - 10 = 10º

B = 4*10 + 40 = 80º.

- Exercício 3

Determinar os valores dos ângulos A e B da Parte III) da Figura 3.

Solução

A figura é cuidadosamente analisada para procurar ângulos complementares. Nesse caso, você tem que + b = 90 graus. Substituindo a expressão de A e B em função de X dada na figura, você tem:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Dividir os dois membros por 3 é o seguinte:

x + 10 = 30

Onde se segue que x = 20º.

Ou seja, o ângulo A = -20 +45 = 25º. E por sua parte: b = 4*20 -15 = 65º.

Ângulos de lados perpendiculares

Dizem que dois ângulos são lados perpendiculares Se cada lado tiver sua perpendicular correspondente no outro. A figura a seguir esclarece o conceito:

Pode atendê -lo: sucessão composta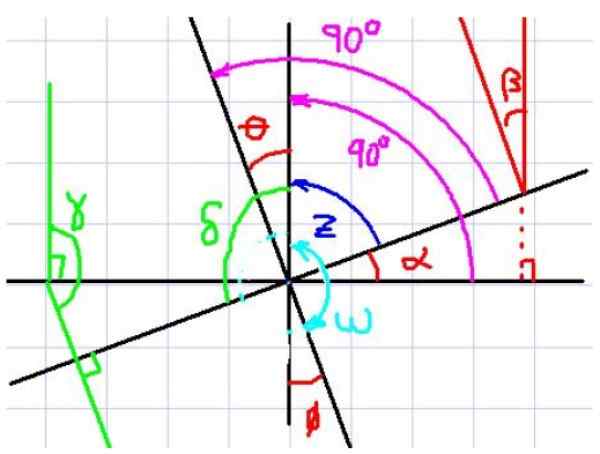Figura 4. Ângulos de lados perpendiculares. Fonte: f. Zapata.

Na Figura 4, os ângulos α e θ são observados, por exemplo. Agora observe que cada ângulo tem sua perpendicular correspondente no outro ângulo.

Também se vê que α e θ têm o mesmo ângulo complementar z, Portanto, o observador conclui imediatamente que α e θ têm a mesma medida. Parece então que se dois ângulos têm lados perpendiculares, eles são iguais, mas vamos ver outro caso.

Agora considere os ângulos α e ω. Esses dois ângulos também têm lados perpendiculares correspondentes, no entanto, não se pode dizer que eles são de igual medida, uma vez que um é agudo e o outro é obtuso.

Observe que ω + θ = 180º. Além de θ = α. Se você substituir esta expressão de z na primeira equação que obtém:

Δ + α = 180º, sendo que δ e α são ângulos de lados mutuamente perpendiculares.

Regra geral para ângulos de lados perpendiculares 

Do acima mencionado, uma regra que sempre é cumprida de que os ângulos têm lados perpendiculares podem ser estabelecidos:

Se dois ângulos são lados mutuamente perpendiculares, eles são iguais se ambos forem agudos ou ambos obtusos. Caso contrário, se um for agudo e o outro é obtuso, é suplementar, ou seja, eles adicionam 180º.

Aplicando esta regra e em referência aos ângulos da Figura 4, podemos afirmar o seguinte:

α = β = θ = φ

γ = δ

Com o ângulo suplementar ω de α, β, θ e φ.

Referências

1. Baldor, J. PARA. 1973. Geometria plana e espacial. Cultural da América Central. 
2. Leis e fórmulas matemáticas. Sistemas de medição de ângulo. Recuperado de: IngeMecanica.com.
3. Wentworth, G. Geometria do Planeta. Recuperado de: Gutenberg.org.
4. Wikipedia. Ângulos complementares. Recuperado de: é.Wikipedia.com
5. Wikipedia. Transportador. Recuperado de: é.Wikipedia.com
6. Zapata f. Goniômetro: história, peças, operação. Recuperado de: Lifer.com