Série de exemplos de poder e exercícios

A Série de Power Consiste em uma soma de termos na forma de poderes da variável x, ou mais geralmente, de X-C, onde c É um número real constante. No resumo da soma, uma série de poderes é expressa da seguinte maneira:

∑a_n (X -c)ⁿ = a_qualquer + para₁ (x - c) + A₂ (X - C)² + para₃ (X - C)³ +… + A_n (X - C)ⁿ

Onde os coeficientes para_qualquer, para₁, para₂… São números reais e a série começa em n = 0.

figura 1. Definição de uma série de poder. Fonte: f. Zapata.

Esta série está focada no valor c isso é constante, mas você pode escolher isso c Seja igual a 0, nesse caso, os poderes são simplificados:

∑a_n xⁿ = a_qualquer + para₁ x + a₂ x² + para₃ x³ +… + A_n xⁿ

A série começa com para_qualquer(X-C)⁰ e para_qualquerx⁰ respectivamente. Mas sabemos disso:

(X-C)⁰= x⁰ = 1

Portanto para_qualquer(X-C)⁰ = para_qualquerx⁰ = para_qualquer (Termo independente)

O bom dos poderes dos poderes é que, com eles, você pode expressar funções e isso tem muitas vantagens, especialmente se você quiser trabalhar com uma função complicada.

Quando esse é o caso, em vez de usar diretamente a função, seu desenvolvimento de poder é usado, que pode ser mais fácil de derivar, integrar ou trabalhar numericamente.

Claro que tudo está condicionado à convergência da série. Uma série converge quando, adicionando uma certa quantidade de termos, um valor fixo é obtido. E se adicionarmos mais termos, continuaremos a obter esse valor.

[TOC]

Funciona como poderes de poderes

Como exemplo de uma função expressa como uma série de poder, vamos tomar f (x) = e^x.

Esta função pode ser expressa em termos de uma série de poderes da seguinte maneira:

e^x  ≈ 1 + x + (x² / 2!) + (X³ / 3!) + (x⁴ / 4!) + (x⁵ / 5!) +..

Onde! = n. (N-1). (N-2). (N-3)… e é levado 0! = 1.

Vamos verificar com a ajuda de uma calculadora, que a série coincide efetivamente com a função explicitamente dada. Por exemplo, vamos começar a fazer x = 0.

Pode servir a você: probabilidade teórica: como divulgá -lo, exemplos, exercícios

Nós sabemos que e⁰ = 1. Vamos ver o que a série faz:

e⁰ ≈ 1 + 0 + (0² / 2!) + (0³ / 3!) + (0⁴ / 4!) + (0⁵ / 5!) +… = 1

E agora vamos tentar com x = 1. Uma calculadora joga isso e¹ = 2.71828, E então vamos comparar com a série:

e¹ ≈ 1 + 1 + (1² / 2!) + (1³ / 3!) + (1⁴ / 4!) + (1⁵ / 5!) +… = 2 + 0.5000 + 0.1667 + 0.0417 + 0.0083 +… ≈ 2.7167

Com apenas 5 termos, já temos uma coincidência exata em e ≈ 2.71. Nossa série está faltando um pouco mais, mas à medida que mais termos são adicionados, com toda a certeza a série converge para o valor exato de e. A representação é exata quando N → ∞.

Se a análise anterior for repetida para n = 2 Resultados muito semelhantes são obtidos.

Dessa maneira, temos certeza de que a função exponencial f (x) = e^x Pode ser representado por esta série de poderes:

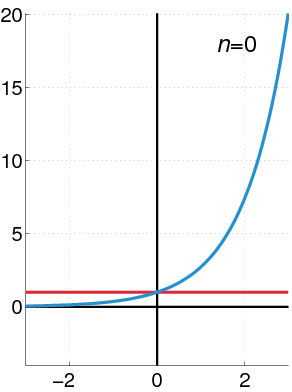Figura 2. Nesta animação, é vista como os poderes estão mais próximos da função exponencial à medida que mais termos são tomados. Fonte: Wikimedia Commons.

Poderes geométricos de poderes

A função f (x) = e^x Não é a única função que admite uma representação em série de poderes. Por exemplo, a função  F(x) = 1/1 - x  Parece muito com o conhecido Série geométrica convergente:

∑a.rⁿ = A / 1 - R

Basta fazer a = 1 e r = x para obter uma série adequada para esta função, que está centrada em c = 0:

No entanto, sabe -se que esta série é convergente para │r│<1, por lo tanto la representación es válida únicamente en el intervalo (-1,1), aunque la función sea válida para todo x, excepto x=1.

Quando você deseja definir essa função em outro intervalo, ela simplesmente se concentra em um valor adequado e pronto.

Como encontrar o desenvolvimento da série de poderes de uma função

Qualquer função pode ser desenvolvida em uma série de poderes focados em C, desde que você tenha derivado de todos os pedidos em x = c. O procedimento utiliza o seguinte teorema, chamado Teorema de Taylor:

Seja f (x) uma função com derivados de ordem n, denotado como F^(N), que admite um desenvolvimento em série de poderes no intervalo Yo. Seu desenvolvimento em Série Taylor é:

Pode atendê -lo: qual é a localização de números inteiros e decimais?

De maneira que:

f (x) = f (c) + f '(c) (x-c) + f "(c) (x-c)² /2 + f "(c) (x-c)³ /6 +… r_n

Onde r_n, que é o enésimo da série, é chamado resíduo:

Quando c = 0 a série é chamada Série MacLaurin.

Esta série dada aqui é idêntica à série dada no início, só agora existe uma maneira de encontrar explicitamente os coeficientes de cada termo, dado por:

No entanto, deve -se garantir que a série transmita a função que você deseja representar. Acontece que nem todas as séries Taylor necessariamente converge para o f (x) que era em mente ao calcular os coeficientes para_n.

Isso acontece porque talvez aqueles derivados da função, avaliados em x = c coincidir com o mesmo valor daqueles derivados de outro, também em x = c. Nesse caso, os coeficientes seriam os mesmos, mas o desenvolvimento seria ambíguo por não ter a certeza de qual função corresponde.

Felizmente, existe uma maneira de saber:

Critérios de convergência

Para evitar a ambiguidade, se r_n → 0 Quando n → ∞ para todos os x no intervalo i, a série converge para f (x).

Exercício

- Exercício resolvido 1

Encontre os poderes geométricos para a função f (x) = 1/2 - x focado em c = 0.

Solução

A função dada deve ser expressa de uma maneira que corresponda o máximo possível com 1/1- x, cuja série é conhecida. Portanto, reescrevemos o numerador e o denominador, sem alterar a expressão original:

1/2 - x = (1/2) / [1 - (x / 2)]

Como ½ é constante, ele sai da soma, e isso é escrito em termos da nova variável x/2:

Pode servir a você: Binomial conjugado: como é resolvido, exemplos, exercícios

Observe que x = 2 não pertence ao domínio da função e de acordo com os critérios de convergência dados na seção Série geométrica de potência, O desenvolvimento é válido para │x/2│< 1 o equivalentemente -2 < x < 2.

- Exercício resolvido 2

Encontre os 5 primeiros termos do desenvolvimento da série de Maclaurin da função f (x) = sen x.

Solução

Passo 1

Primeiro são os derivados:

-Derivado da Ordem 0: É a mesma função f (x) = sen x

-Primeiro derivado: (sin x) '= cos x

-Segunda derivada: (sin x) "= (cos x) '= - sin x x

-Terceira derivada: (sin x) "= (-sen x) '= - cos x

-Quarto derivado: (sin x) "= (- cos x) '= sin x x

Passo 2

Em seguida, cada derivado é avaliado em x = c, assim como um desenvolvimento de maclaurina, c = 0:

sin 0 = 0; cos 0 = 1; - sen 0 = 0; -Cos 0 = -1; sin 0 = 0

etapa 3

Os coeficientes são construídos para_n;

para_qualquer = 0/0! = 0; para₁ = 1/1! = 1; para₂ = 0/2! = 0; para₃ = -1 / 3!; para₄ = 0/4! = 0

Passo 4

Finalmente a série é montada de acordo com:

sin x ≈ 0.x⁰ + 1. x¹ + 0 .x² - (1/3!) x³ + 0.x⁴... = x - (1/3!)) x³  +..

O leitor precisa de mais termos? Quantos mais, a série está mais próxima da função.

Observe que existe um padrão nos coeficientes, o seguinte termo não -nulo é para₅ E todo o índice ímpar também é diferente de 0, alternando os sinais, para que:

Sen x ≈ x - (1/3!)) x³  + (1/5!)) x⁵ - (1/7!)) x⁷  +.. .

É deixado como exercício para verificar, você pode usar o proporção do quociente Para convergência em série.

Referências

1. Fundação CK-12. Série de Power: Representação de Funções e Operações. Recuperado de: CK12.org.
2. Engler, a. 2019. Cálculo integral. Universidade Nacional da Costa.
3. Larson, r. 2010. Cálculo de uma variável. 9NA. Edição. McGraw Hill.
4. Textos de matemática gratuitos. Série de Power. Recuperado de: matemática.Liibretexts.org.
5. Wikipedia. Série de Power. Recuperado de: é.Wikipedia.org.