Regra de ressecros

Explicamos qual é a regra de Sturges, sua aplicação e damos vários exemplos

Qual é a regra de Sturges?

O Regra de ressecros É um critério usado para determinar o número de classes ou intervalos necessários para representar graficamente um conjunto de dados estatísticos graficamente. Esta regra foi declarada em 1926 pelo matemático alemão Herbert Sturges.

Sturges propuseram um método simples, com base no número de amostras X que permitiram encontrar o número de classes e sua gama de intervalo. A regra Sturges é amplamente utilizada acima de tudo na área de estatística, especificamente para construir histogramas de frequência.

Explicação

A regra Sturges é um método empírico amplamente utilizado em estatísticas descritivas para determinar o número de classes que devem existir em um histograma de frequência, a fim de classificar um conjunto de dados que representam uma amostra ou população.

Basicamente, esta regra determina a largura de recipientes gráficos, histogramas de frequência.

Para estabelecer sua regra, Herbert Sturges considerou um diagrama de frequência ideal, que consiste em K intervalos, onde o intervalo i -este contém um certo número de amostras (i = 0,… k - 1), representado como:

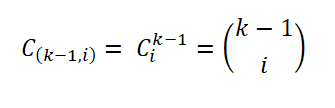
Esse número de amostras é dado pelo número de maneiras pelas quais um subconjunto de um conjunto pode ser extraído; isto é, pelo coeficiente binomial, expresso da seguinte forma:

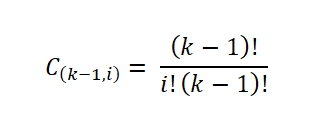Em seguida, ressecros relacionados que o histograma de frequência se aproximará de uma distribuição normal quando o número de intervalos (k) aumentar de acordo com o teorema central do limite. De tal maneira que o número de amostras de cada um dos intervalos pode ser calculado:

Pode atendê -lo: Enegon: Propriedades, como fazer um Enegon, exemplos

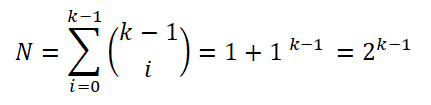
Para simplificar a expressão, ele aplicou as propriedades dos logaritmos em ambas as partes da equação:

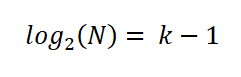
Assim, Sturges estabeleceu que o número ideal de intervalos K é dado pela expressão:

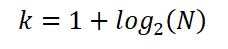
Também pode ser expresso como:

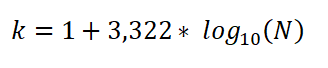
Nesta expressão:

• K é o número de classes.
• N é o número total de observações na amostra.
• O log é o logaritmo base comum 10.

Por exemplo, para elaborar um histograma de frequência que expressa uma amostra aleatória da estatura de 142 crianças, o número de intervalos ou classes que a distribuição terá é:

K = 1 + 3.322 _* registro₁₀ (N)

K = 1+3.322_* Log (142)

K = 1+3.322_* 2.1523

K = 8,14 ≈ 8

Assim, a distribuição será em 8 intervalos.

O número de intervalos deve sempre ser representado por números inteiros. Nos casos em que o valor é decimal, uma aproximação deve ser feita para o número inteiro mais próximo.

Aplicações de regra de Sturges

A regra Sturges é aplicada principalmente em estatísticas, pois permite uma distribuição de frequência através do cálculo do número de classes (k), bem como o comprimento de cada uma delas, também conhecida como amplitude.

A amplitude é a diferença no limite superior e inferior da classe, dividido pelo número de classes, e é expresso:

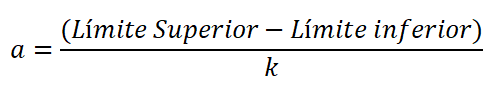
Existem muitas regras empíricas que permitem uma distribuição de frequência. No entanto, a regra de ressecros é comumente usada porque faz uma aproximação do número de classes, que geralmente vai de 5 a 15.

Dessa maneira, considera um valor que representa adequadamente uma amostra ou população; Ou seja, a abordagem não representa grupos extremos, nem funciona com um número excessivo de classes que não permitem resumir a amostra.

Pode atendê -lo: ângulos opostos pelo vértice (com um exercício resolvido)

Exemplo

Um histograma de frequência precisa ser realizado de acordo com os dados fornecidos, que correspondem a idades obtidas em uma pesquisa de homens que se exercitam em um ginásio local.

Para determinar os intervalos, o tamanho da amostra ou o número de observações deve ser conhecido; Nesse caso, existem 30.

Então a regra de Sturges se aplica:

K = 1 + 3.322 _* registro₁₀ (N)

K = 1+3.322_* Log (30)

K = 1+3.322_* 1.4771

K = 5,90 ≈ 6 intervalos.

A partir do número de intervalos, você pode calcular a amplitude que eles terão; isto é, a largura de cada barra representada no histograma de frequência:

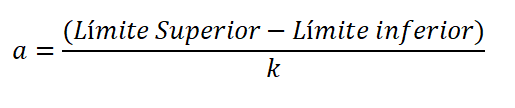
O limite inferior é considerado como o valor mais baixo dos dados, e o superior é o valor mais alto. A diferença entre o limite superior e inferior é chamada de alcance ou rota da variável (r).

A tabela tem que o limite superior é 46 e os 13 inferiores; Dessa forma, a amplitude de cada classe será:

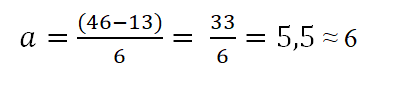
Os intervalos serão compostos de um limite superior e inferior. Para determinar esses intervalos, começa contando a partir do limite inferior, adicionando a isso a amplitude determinada pela regra (6), da seguinte forma:

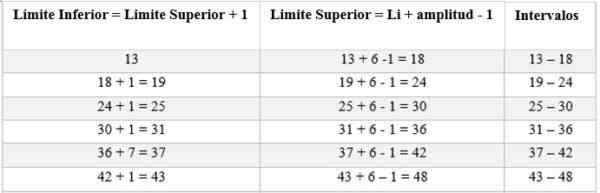
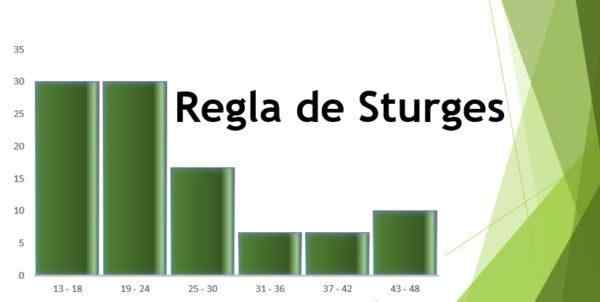
Então a frequência absoluta é calculada para determinar o número de homens que correspondem a cada intervalo; Nesse caso, é:

• Intervalo 1: 13 - 18 = 9
• Intervalo 2: 19 - 24 = 9
• Intervalo 3: 25 - 30 = 5
• Intervalo 4: 31 - 36 = 2
• Intervalo 5: 37 - 42 = 2
• Intervalo 6: 43 - 48 = 3

Ao adicionar a frequência absoluta de cada classe, isso deve ser igual ao número total da amostra; Neste caso, 30.

Pode atendê -lo: homotecia negativa

Posteriormente, a frequência relativa de cada intervalo é calculada, dividindo a frequência absoluta disso pelo número total de observações:

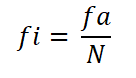
• Intervalo 1: fi = 9 ÷ 30 = 0,30
• Intervalo 2: fi = 9 ÷ 30 = 0,30
• Intervalo 3: fi = 5 ÷ 30 = 0,1666
• Intervalo 4: fi = 2 ÷ 30 = 0,0666
• Intervalo 5: fi = 2 ÷ 30 = 0,0666
• Intervalo 4: fi = 3 ÷ 30 = 0,10

Em seguida, você pode fazer uma tabela que reflita os dados e também o diagrama da frequência relativa em relação aos intervalos obtidos, como pode ser visto nas seguintes imagens:

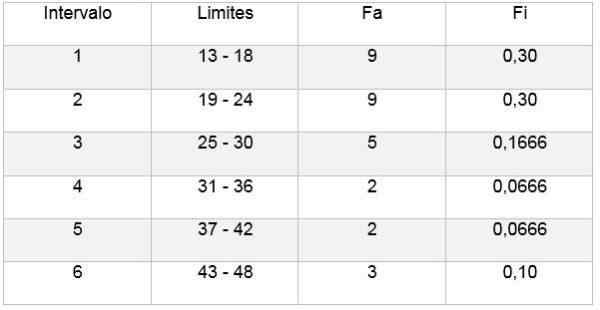
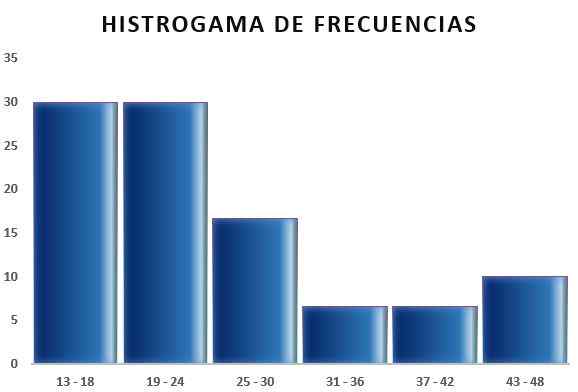
Dessa maneira, a regra Sturges permite determinar o número de classes ou intervalos em que uma amostra pode ser dividida, a fim de resumir uma amostra de dados através da elaboração de tabelas e gráficos.