Regra da alavanca

Qual é a regra da alavanca?

O regra da alavanca É um procedimento matemático que permite calcular as frações, porcentagens ou valores das fases presentes em equilíbrio dentro de um sistema binário. Não é apenas matemático, mas também bastante gráfico e assertivo, sendo muito útil em cálculos físico -químicos e de engenharia.

Esta regra se aplica a diagramas de fase para sistemas binários, independentemente do tipo de sistema. Isto é, as fases podem ser sólidas, como nas ligas; ou líquido e gasoso, como vemos em sistemas em equilíbrio de vapor líquido.

O princípio físico e matemático da alavanca também é usado para fins químicos e na física dos materiais. Fonte: Jimbowley, CC BY-SA 3.0, via Wikimedia Commons

A regra da alavanca pode ser aplicada diretamente levando em consideração os valores gráficos no eixo da abcissa, onde as frações globais ou porcentagens do componente mais volátil geralmente estão indo, no caso de líquidos; ou refratário, no caso de metais em suas ligas.

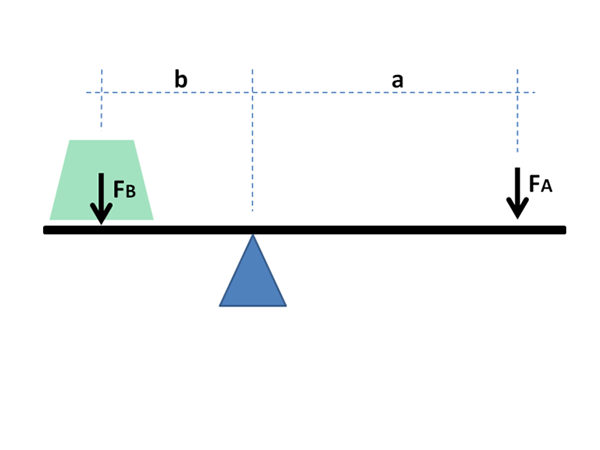
Como será visto abaixo, seu nome se deve à imensa similaridade que tem com as expressões matemáticas que demonstram o equilíbrio entre duas massas localizadas nas extremidades de um roqueiro com Fulcro.

Os braços da alavanca devem equilibrar para equilibrar as massas das cargas; No caso de diagramas de fase, frações e toupeiras das fases no equilíbrio do material.

Explicação

Aspectos gráficos

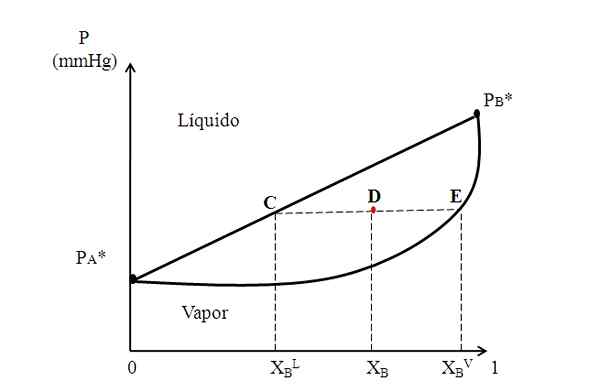Diagrama binário hipotético, onde uma linha de ligação mostra as composições das fases líquidas e de vapor. Fonte: Gabriel Bolívar.

No meio do diagrama acima, temos uma região onde o líquido e o vapor coexistem; isto é, a região de equilíbrio de vapor líquido. Acima desta região, a mistura de A e B será líquida e, por baixo, será refrigerante por causa das pressões mais baixas.

Agora, considere uma mistura com uma composição X_B e cuja pressão o posiciona no ponto D. Nós desenhamos do ponto d uma linha horizontal que toca a linha e a curva nas laterais, originando pontos C e E, respectivamente. Essa linha, que comunica os pontos C, D e E, C-D-E, é a que a linha da união e projetando-a em direção ao eixo e deve nos dar a pressão do sistema.

Pode servir a você: alcalinidade da água: o que é, determinação e importância

Então, a partir desses pontos, desenhamos outras linhas perpendiculares à linha de ligação, que jogará o eixo x. À medida que o ponto E repousa na curva de vapor, teremos a fração molar de B na fase de vapor (x_B^V). Da mesma forma, o ponto C, na linha reta do líquido, nos dará a fração molar de B na fase líquida (x_B^eu).

A regra da alavanca é baseada com precisão na linha de ligação e nas distâncias entre x_B^eu, X_B e x_B^V.

Dedução matemática

A fração molar global de B é igual a:

X_B = n_B / (n^eu + n^V)

Onde n_B Eles são o total de toupeiras de B tanto na fase líquida quanto no vapor, e n^eu e n^V são as respectivas toupeiras para essas fases. Limpeza n_B nós teremos:

n_B = X_Bn^eu + X_Bn^V (1)

Por outro lado, n_B Também é igual a:

n_B = n_B^eu + n_B^V

= X_B^eun^eu + X_B^Vn^V  (2)

Agora, equalizando as equações (1) e (2) nos darão:

X_Bn^eu + X_Bn^V = X_B^eun^eu + X_B^Vn^V

E reorganizar:

n^eu(X_B - X_B^eu) = n^V(X_B^V - X_B) (3)

n^eu(C-d) = n^V(DE)

Essas duas últimas expressões matemáticas são a regra da alavanca. Observe que x_B - X_B^eu É a distância entre os pontos C e D; e x_B^V - X_B, É a distância entre os pontos D-E: as duas metades da linha de ligação (braços da alavanca).

Esta equação é muito semelhante à que descreve o equilíbrio das massas em um roqueiro com Fulcro:

m₁eu₁ = m₂eu₂

Assim, a regra da alavanca nos permitirá calcular as toupeiras totais n^eu e n^V desde que o total de moles da mistura seja conhecido, n_T (n_T = n^eu + n^V).

Segunda forma

A expressão anterior da regra da alavanca serve para calcular as quantidades (massas, toupeiras, etc.) das fases em equilíbrio. No entanto, a versão mais conhecida da regra da alavanca nos permite calcular as frações ou porcentagens de cada fase, levando apenas as distâncias entre x_B, X_B^eu e x_B^V.

Considere o mesmo sistema acima, tendo outra forma da regra da alavanca:

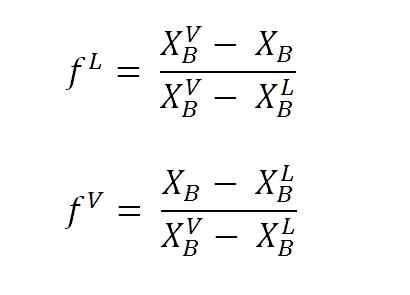Equações para calcular frações líquidas e vapor usando os braços da alavanca. Fonte: Gabriel Bolívar.

Onde F ^eu e F ^VSão frações molares (ou porcentagem, dependendo do gráfico) das fases de líquido e vapor, respectivamente. Observe que, obviamente, F ^eu e F ^V Eles não têm unidades; enquanto que n^eu e n^V Sim, eles têm unidades (toupeiras, gramas, etc.).

Pode atendê -lo: calor de reação

Exemplos

Método 1

Em um recipiente 28 moles de B e 12 moles de A são misturados. Determinar as quantidades e frações molares para as fases que são formadas.

Calculamos x_B:

X_B = (28 moles b)/ (28 moles b + 12 moles a)

= 0.7

Este valor corresponde a x_B do diagrama superior. As interceptações nos darão aproximadamente os seguintes valores para x_B^eu e x_B^V:

X_B^eu = 0.41

X_B^V = 0.94

Com a regra da alavanca:

n^eu(X_B - X_B^eu) = n^V(X_B^V - X_B)

E sabendo disso n_T = n^eu + n^V, e que n_T = 40 moles, então limpamos n^eu qualquer n^V Dependendo do outro:

n^eu(X_B - X_B^eu) = (40 moles - n^eu) (X_B^V - X_B)

Reorganização e limpeza n^eu nós teremos:

n^eu = (40 moles) (x_B^V - X_B) / (X_B^V - X_B^eu)

Essa expressão não se lembra da de F ^eu? Agora substituindo que teremos:

n^eu = (40 moles) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 toupeiras na fase líquida

Podemos calcular n^V De duas maneiras:

n^V = n^eu(X_B - X_B^eu) / (X_B^V - X_B)

qualquer

n^V = 40 toupeiras - 18.11 toupeiras

= 21.89 toupeiras na fase de vapor

Método 2

E se calculamos primeiro F ^eu e F ^V?

F ^eu = (X_B^V - X_B) / (X_B^V - X_B^eu)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 ou 45.28%

Isto é, 45.2% das toupeiras estão em fase líquida, sendo essa quantia igual a:

n^eu = F ^eun_T

= (0.4528) (40 moles)

= 18.11 toupeiras

E F ^V Podemos calculá -lo igualmente de duas maneiras:

F ^V = 1 - F ^eu

qualquer

F ^V = (X_B - X_B^eu) / (X_B^V - X_B^eu)

Sendo seu valor:

F ^V = 0.5472 ou 54.72%

E, por conseguinte, n^V Será igual a:

n^V = F ^Vn_T

= (0.5472) (40 moles)

= 21.89 toupeiras

Observe que a aplicação dos dois formulários da regra da alavanca como métodos de cálculo alternativos, os mesmos resultados podem ser alcançados. O método 2 parece mais direto e simples; mas se for observado com cuidado, uma vez que a clareira for resolvida n^eu qualquer n^V, Veremos que ambos os métodos são realmente igualmente fáceis.

Exercícios resolvidos

Em seguida, dois outros exercícios serão resolvidos, onde agora os sistemas considerados envolverão um vporte líquido e sólido e não-líquido. Além disso, os diagramas são gráficos em relação à temperatura do sistema e não sua pressão.

Exercício 1

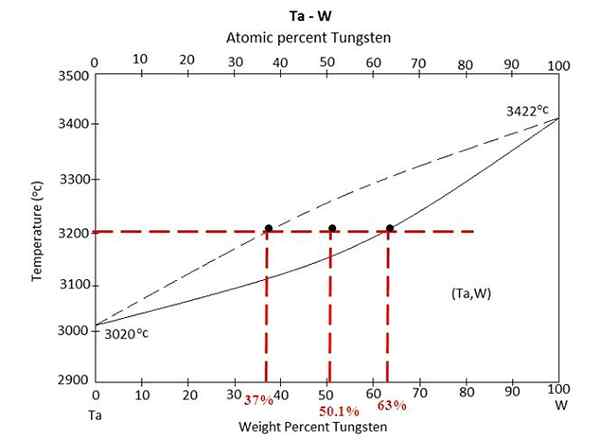Diagrama de fases para uma liga entre Tantalo e Tungstênio. Fonte: Materialspedia, CC BY-SA 4.0, via Wikimedia Commons

Temos o diagrama de fases acima de uma liga entre Tantalo e Tungstênio, Ta-W. No eixo x as porcentagens de massa global de tungstênio, w% (m/m) são representadas.

Dentro da região de equilíbrio líquido (ta+w) e sólido (liga), há uma mistura a 3200 ºC. Determinar as massas de cada fase assumindo que 100 gramas da liga foram aquecidos.

Pode servir a você: metais, não -metais e metalóides

Procedimento

Desta vez, o exercício será resolvido usando a segunda forma da regra da alavanca. A linha da União nos diz que: Na fase sólida, temos 63% de tungstênio, enquanto na fase líquida temos 37% de tungstênio. Isso ocorre porque o tungstênio derrete a uma temperatura mais alta (3422 ºC) do que o tantal (3020 ºC).

Então nós temos:

C%^S ou w_S= 63%

C%^eu ou w_eu= 37%

E também:

C₀ = 50.1%

Aplicamos a regra da alavanca para F ^eu:

F ^eu = (63% - 50.1%) / (63% - 37%)

= 0.4961 ou 49.61%

Observe que a distância correspondente à fase líquida é o braço da alavanca próximo à fase sólida, o lado oposto do ponto médio.

A massa da fase líquida é, portanto:

(0.4961) (100 gramas) = ​​49.61 gramas fundidas

E a fase sólida será igual a:

100 gramas - 49.61 gramas = 50.39 gramas de liga rica em tungstênio

Exercício 2

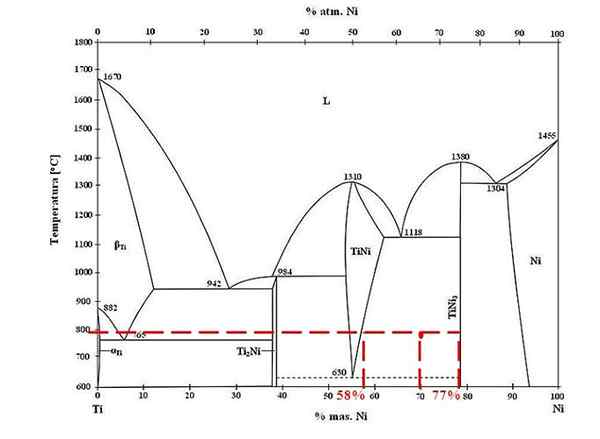Diagrama de fases para ligas de titânio-níquel. Fonte: Doomger, CC BY-SA 3.0, via Wikimedia Commons

Para a liga de titânio e níquel a 800 ºC e com 70% de níquel, determine quanto de tini e tini₃ estão presentes.

Procedimento

Desta vez, eles só pedem as frações de massa de cada fase. O ponto vermelho está localizado na região de equilíbrio entre as fases de tini e tini₃, cujas curvas é onde toca a linha de união que flui para os valores de 58% ou para a fase de tini e 77% ou para a fase tini₃.

Observe que o ponto vermelho está mais próximo da fase tini₃ o da fase de tini. Isso significa que deve haver mais tini₃ aquele tini; E, portanto, a distância ou o braço da alavanca correspondente a tini₃ Deve ser o mais longo, o oposto (70%-58%).

Sabendo disso, passamos a calcular F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 ou 63.16%

De fato, 63.16% da liga corresponde à fase tini₃. Enquanto isso, a fase tini corresponde a:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 ou 36.84%

Em conclusão dos exercícios levantados, podemos dizer que a regra da alavanca é muito útil para determinar as frações de cada fase em equilíbrio para um sistema de dois componentes.

Referências

1. Walter J. Moore. (1963). Química Física. Em cinética química. Quarta edição, Longmans.
2. Irã. Levine. (2009). Princípios da físico -química. Sexta edição. Mc Graw Hill.
3. Wikipedia. (2020). Regra da alavanca. Recuperado de: em.Wikipedia.org
4. Michael Adewumi. (18 de maio de 2020). A regra da alavanca. Recuperado de: Eng.Librettexts.org
5. Adam Warren. (1997). Diagramas de fase: linhas de ligação e a regra da alavanca. Recuperado de: Southampton.AC.Reino Unido
6. Universidade de Cambridge. (2020). A regra da alavanca. Recuperado de: Doitpoms.AC.Reino Unido