Reatância indutiva

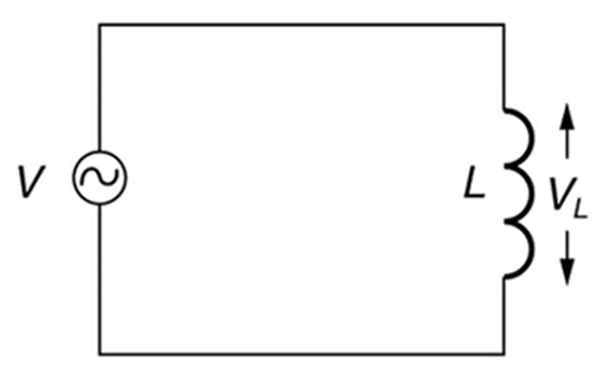
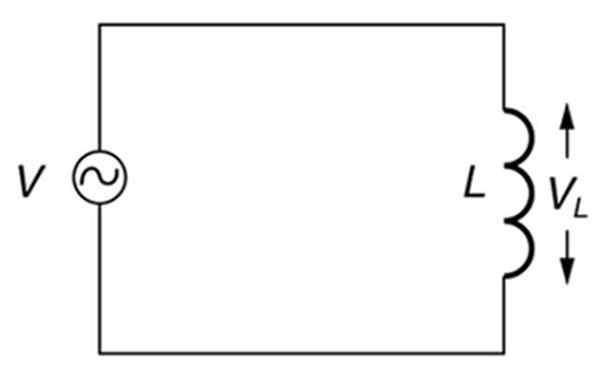Um circuito alternativo puramente indutivo. Fonte: Open Stax. Física da faculdade.

O que é reatância indutiva?

O Reatância indutiva Refere -se à oposição apresentada pela bobina à passagem da corrente, em um circuito alternativo. Em outras palavras, é a capacidade do indutor de reduzir a corrente em um circuito alternativo. Indicado como x_eu, Seu valor depende da indutância e da frequência angular da tensão:

X_eu= Ω ∙ l

Onde ω é a frequência angular em radianos/s e l indutância, medida em Henrios (H) no sistema internacional de unidades se.

Grandes indutâncias produzem grande reatância indutiva, uma vez que sua resistência à mudança é maior. E a reatância também aumenta com a frequência; portanto, uma certa indutância L produzirá maior reatância, quanto maior a frequência de tensão.

A unidade de reatância indutiva é o Ohmio, simbolizado por ω. É a mesma unidade de resistência elétrica, mas diferente disso, x_eu Não é constante, pois depende da frequência da tensão alternativa aplicada.

Portanto, em um circuito cujos únicos elementos são uma fonte alternativa e uma indutância (circuito indutivo), como o mostrado na figura acima, a reatância indutiva dependerá da frequência da fonte.

No entanto, a analogia de X_eu Com resistência elétrica, pode ser estendido ao circuito indutivo, permitindo a aplicação da lei de Ohm. Se x for definido_eu Como a proporção entre as amplitudes de tensão V_eu No indutor e o atual eu_eu que atravessa:

X_eu = V_eu / Yo_eu

Você pode escrever a Lei OHM para circuitos puramente indutivos da seguinte forma:

V_eu = X_eu∙ i_eu

Fórmulas de reatância indutiva

Para calcular a reatância indutiva, é usada a fórmula dada no início, na qual L representa a indutância (Henrios) e ω é a frequência angular (radianos/segundo):

Pode servir a você: Millikan Experiment: Procedimento, Explicação, Importância

X_eu= Ω ∙ l

É comum que a frequência seja expressa em Hertz ou Hertzio (Hz). Nesse caso, é indicado por f e está relacionado à frequência angular através da fórmula:

Ω = 2π ∙ f

Nesse caso, a reatância é calculada como:

X_eu= 2πf ∙ l

Em qualquer uma dessas fórmulas, a reatância indutiva resulta em ohms, como explicado anteriormente.

O efeito da indutância em um circuito indutivo

Como a indutância se opõe às mudanças ou variações da corrente, a reatância indutiva é caracterizada pela adiando a onda atual em relação à onda de tensão.

No gráfico a seguir, que mostra a tensão V_eu (Azul) e o atual eu_eu (vermelho) No indutor, ambos sinóidalmente, observa -se que ambas as ondas estão desatualizadas 90º. A partir de t = 0, o valor da tensão é máximo, no entanto, a corrente é zero naquele momento.

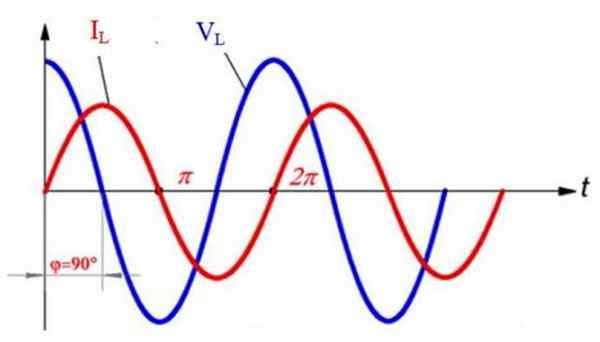Corrente alternativa e tensão em um circuito indutivo. Preparado por: f. Zapata.

Posteriormente, observa -se que a corrente atinge seu valor máximo em t = π /2, mas então a tensão é cancelada e investe sua polaridade, ou seja, torna -se negativa. Simultaneamente, a corrente diminui seu valor, enquanto a tensão se torna cada vez mais negativa.

Posteriormente, em t = π, a tensão atinge sua magnitude máxima, embora com a polaridade invertida, e então a corrente seja cancelada. De tudo isso, segue -se que sempre que V_eu Atinge um pico, a corrente é cancelada e toda vez que a corrente atinge sua magnitude máxima, a tensão é 0.

A corrente sempre atinge seu pico após a tensão, e isso ocorre porque, como afirmado no início, a indutância se opõe aumenta ou diminui.

Pode servir a você: vantagem mecânica: fórmula, equações, cálculo e exemplos

Como calcular a reatância indutiva

Cálculo da reatância indutiva é muito simples: é necessário saber o valor da indutância e a frequência da tensão alternativa aplicada. Em seguida, esses dados são substituídos em uma das fórmulas fornecidas na seção anterior e a operação correspondente é realizada.

Os exemplos a seguir e exercícios resolvidos mostram como fazê -lo em várias situações.

Exemplos

Exemplo 1

Suponha que A L = 5 Mh Indutor, ao qual uma tensão de frequência alternativa é aplicada 60.0 Hz. A reatância indutiva neste caso é calculada por:

X_eu= 2πf ∙ l

Mas antes de substituir os valores, a indutância deve se tornar Henrios, multiplicando pelo fator 1 × 10^-3. Portanto:

L = 5 × 10^-3 H

Então:

X_eu= 2πf ∙ l = x_eu= 2π × 60 Hz × 5 × 10^-3 H = 1. 88 ohm

Exemplo 2

Agora a mesma indutância está conectada a uma tensão de frequência alternativa diferente: 10.0 kHz. Nesse caso, a indutância apresenta uma maior reatância:

X_eu= 2πf ∙ l = x_eu= 2π × 10.0 × 10³ Hz × 5 × 10^-3 H = 314.2 ohm

Exemplo 3

A tensão aplicada à indutância dos Exemplos 1 e 2 tem um valor de 120 V rms. A respectiva corrente RMS é determinada através da lei ohm v_eu = X_eu∙ i_eu:

Yo_eu = V_eu / X_eu

Para a frequência de 60.0 Hz, a corrente é:

Yo_eu = 120 v / 1. 88 ohm = 63.8 a

E para a frequência de 10.0 kHz:

Yo_eu = 120 v / 314.2 ohm = 0.38 a

Como neste último caso a reatância é muito maior, espera -se que a corrente seja menor. Essa propriedade faz do indutor um filtro de alta frequência, um recurso usado para reduzir sons de alta frequência em equipamentos de som ou para proteger os dispositivos de altos atuais repentinos, entre outras aplicações.

Pode servir a você: Teorema de Steiner: Explicação, Aplicações, Exercícios

Exercícios resolvidos

Exercício 1

Determinar a reatância indutiva em um circuito que consiste em uma indutância de 2.5 MH, em série com uma fonte de tensão alternativa, cuja frequência é 75 r.p.m.

Solução

Uma revolução ou ciclo completo é igual a 2π radianos e um minuto tem 60 segundos, portanto, uma frequência de 75 r.p.M é equivalente a:

75 r.p.M = 75 × 2π radianos / 60 segundos = 7.85 radianos/s

E com esse valor, a reatância é:

X_eu= Ω ∙ l = (7.85 radianos/s) × 2.5 × 10^-3 H = 0.02 Ω

Exercício 2

A indutância serial é usada com a fonte de um computador para filtrar o ruído de altas frequências.

a) Qual deve ser o valor mínimo de indutância necessário para produzir uma reatância de 2 kΩ, se a frequência do sinal que é filtrar for de 15 kHz?

b) Encontre a reatância deste indutor na frequência de 60 Hz.

Solução para

X_eu = 2 kΩ = 2000 Ω

F = 15 kHz = 15000 Hz

Portanto, a limpeza da equação x_eu= 2πf ∙ l, você tem:

L = x_eu / 2π ∙ f = 2000 Ω / 2π × 15000 Hz = 0.0212 h = 21.2 mh

Solução b

Usando x novamente_eu= 2πf ∙ l, mas com f = 60 Hz, resultados:

X_eu= 2π × 60 Hz × 0.0212 h = 8 ohm.

Referências

1. Bauer, w. (2011). Física para engenharia e ciências. Volume 1. Mc Graw Hill. 
2. Giancoli, d. (2006). Física: Princípios com aplicações. 6º. Ed Prentice Hall.
3.  Katz, d. (2013). Física para cientistas e engenheiros. Fundações e conexões. Cengage Learning.
4. Stax aberto. Física da faculdade. Recuperado de: OpenStax.org.
5. Sears, z. (2016). Física da Universidade com Física Moderna. 14º. Ed. Volume 2. Pearson