Razão para mudar

Qual é o motivo da mudança?

O razão para mudar É a magnitude matemática que define a mudança de uma variável ou de uma magnitude física em relação a outra. Por exemplo, a velocidade é a razão para mudar a posição em relação ao tempo.

Uma mudança em uma magnitude x, Ele é indicado com as letras gregas δ (diz “delta”) e está escrito Δx. É calculado pela diferença entre um valor final e um inicial: Δx = x_final- x_inicial.

Se a magnitude x está relacionado a outra magnitude e, Isso também experimenta uma mudança, chamada Δy = y_final- e_inicial, A razão para mudar Y em relação a X é definida como o quociente:

Que, usando a notação com Delta indicada antes, permanece assim:

Este quociente é conhecido como o Aumentar o quociente de e em relação a x qualquer taxa de mudança média ou média.

Dessa maneira, você pode definir magnitudes como o índice de crescimento de uma população, velocidade com que um objeto, taxa de desemprego, o fluxo de água através de um tubo e muito mais. Todas essas quantidades são, na verdade, razões de mudança.

Por que é importante calcular o motivo da mudança?

Numerosas magnitudes de interesse não permanecem imutáveis, mas experimentam mudanças, e muitas vezes essas mudanças se seguem no tempo. Daí a importância de calcular o motivo da mudança de magnitude ao longo do tempo.

Por exemplo, existe o caso simples de um objeto que se move ao longo de uma linha reta, que pode ser o eixo ou eixo horizontal do x. O celular (um carro, uma bicicleta, uma pessoa que anda ou corre ...) muda continuamente sua posição quando o tempo passa t.

Então, a razão para alterar a posição do objeto Δx no intervalo de tempo ΔT é conhecida como velocidade média:

Outro celular que viaja pela mesma linha reta pode fazê -lo com velocidade diferente, seja ou menos, e assim é distinguida do primeiro celular (porque é mais lento ou mais rápido).

Por exemplo, um corredor plano de 100 metros terá uma taxa de câmbio médio em sua posição muito maior que um maratonista ou uma pessoa que caminha silenciosamente pela rua.

A velocidade é um exemplo típico de razão de mudança, mas algumas magnitudes interessantes que também sofrem mudanças no tempo, são: a temperatura, o volume de um fluido, a carga elétrica, uma população de bactérias e muito mais.

Conhecendo o motivo da mudança, você pode saber muito sobre a maneira como essas magnitudes evoluem com o tempo.

Unidades do motivo da mudança

A proporção é a proporção entre duas magnitudes, as unidades resultantes também serão o quociente das unidades usadas para medi -las. Por exemplo, a velocidade é a extensão entre o tempo, pois é a razão para mudar a posição em relação ao tempo.

Dessa forma, as unidades de velocidade podem ser medidores/segundo, quilômetros/hora, milhas/hora e muitas outras combinações.

Como a mudança é calculada?

A razão média ou taxa de câmbio entre duas magnitudes é facilmente calculada ao executar o quociente entre as respectivas variações de cada uma, de acordo com a fórmula:

Alterações nas magnitudes podem ser dadas através de tabelas de estoque ou são determinadas por um gráfico, do qual os respectivos valores de e e x (Veja os exercícios resolvidos no final).

Por outro lado:

E a expressão da direita é precisamente a inclinação de uma linha, da qual conclui -se que o motivo médio da mudança é a inclinação da linha secante para o gráfico de y, dependendo de x.

Sinais do motivo da mudança

De acordo com a definição fornecida, o motivo da mudança pode ser positivo ou negativo, dependendo de como as magnitudes envolvidas variam, pois elas podem aumentar ou diminuir, de acordo com.

Se o motivo da mudança for positivo, significa que mudanças em e e em x Eles eram o mesmo sinal, isso é, e aumentou e x Ele também fez. Ou muito e como x Eles diminuíram.

No entanto, quando o motivo da mudança é negativo, significa que uma das magnitudes aumentou e a outra diminuiu.

Mudança de mudança instantânea

Freqüentemente, é muito mais interessante. Nesse caso, é necessário fazer com que a variação Δx seja extremamente pequena, tendendo a 0 (mas sem se tornar 0, uma vez que a divisão entre 0 não está definida).

Isso é chamado "Tomando o limite" e, nesse caso, a proporção de mudança instantânea é chamada de "derivada" de e em relação a x e é indicado como DY/DX; Então:

A proporção ou taxa de mudança instantânea também é igual à inclinação de uma linha, mas neste caso é a inclinação da linha tangente ao gráfico de e contra x.

Exemplos simples

O crescimento de uma pessoa

Desde que nascem, as crianças crescem em um ritmo determinado por vários fatores, entre os quais genética e comida se destacam. As maiores taxas de crescimento ocorrem durante o primeiro ano de vida; Mais tarde, durante a infância e depois na puberdade, as crianças normalmente experimentam "alongamentos", ou seja, a razão da mudança de altura em relação ao tempo e depois diminuir.

Após a puberdade, os meninos continuam a crescer, mas a taxa diminui até que sejam cancelados, uma vez que atingem sua estatura definitiva de adultos.

Coffee fria

É um fato conhecido que café ou sopa quente são gradualmente resfriados quando deixados à temperatura ambiente. No entanto, a taxa de resfriamento diminui a temperatura mais próxima da temperatura do café ou da sopa à temperatura ambiente.

Uma maneira de modelar esse fenômeno é através Lei de refrigeração de Newton, Segundo o qual, a taxa para a qual o calor é transferido é proporcional à diferença entre a temperatura da substância e a temperatura ambiente. A constante de proporcionalidade k é característica da substância:

T_qualquer representa a temperatura ambiental.

Exercícios resolvidos

Exercício 1

Calcule a taxa média de alteração de e em relação a x, Dados os seguintes valores:

e₁ = 3; e₂ = 10; x₁ = 2; x₂ = 5

Solução

De acordo com a fórmula:

Os valores fornecidos na declaração são substituídos e a operação é resolvida:

Exercício 2

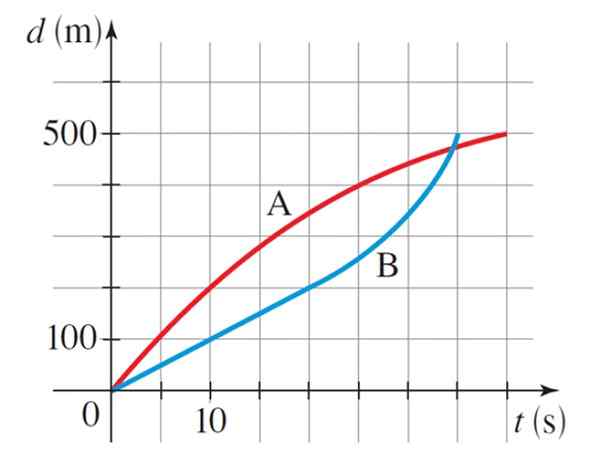
O gráfico mostra as respectivas curvas de distância versus o tempo de dois skatistas de velocidade olímpicos A e B, na modalidade de 500 metros. Quem venceu a corrida? Qual era a velocidade média de cada patinador?

Solução

Observando o gráfico, segue -se que o skatista B (Blue Curve) venceu a corrida, uma vez que visitou 500 m em 35 s, enquanto o skatista A (Curva Vermelha) o fez em 40 s.

As respectivas velocidades médias foram:

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Glencoe Science. Taxa de mudança e inclinação (2021). Recuperado de: glencoe.com.
3. Larson, r. (2012). Pré -cálculo. 8º. Edição. Cengage Learning.
4. Larson, r. (1986). Cálculo com geometria analítica, 2ª. Edição. McGraw-Hill.
5. Stewart, J. (2011). Álgebra, conceitos e contextos da faculdade. Brooks/Cole.