Soma Propriedade Associativa, Multiplicação, Exemplos, Exercícios

O propriedade associativa da soma representa a natureza associativa da operação adiciona vários conjuntos matemáticos. Ele relaciona três (ou mais) elementos desses conjuntos, chamados A, B e C, de modo que sempre sejam cumpridos:

a + (b + c) = (a + b) + c

Dessa forma, é garantido que, independentemente de como agrupar para realizar a operação, o resultado é o mesmo.

figura 1. Usamos a propriedade associativa da soma muitas vezes ao fazer operações aritméticas e algébricas. (Desenho: Freepik Composition: F. Zapata)

Mas deve -se notar que a propriedade associativa não é sinônimo de propriedade comutativa. Isto é, sabemos que a ordem dos adendos não altera a soma ou que a ordem dos fatores não altera o produto. Então, para a soma que você pode escrever assim: a + b = b + a.

No entanto, na propriedade associativa, é diferente, uma vez que a ordem dos elementos a serem adicionados é mantida e o que muda é a operação que é executada primeiro. O que significa que não importa primeiro (B+C) e, para esse resultado.

Muitas operações importantes, como a soma, são associativas, mas não todas. Por exemplo, na subtração de números reais, acontece que:

A - (b - c) ≠ (a - b) - c

Sim a = 2, b = 3, c = 1, então:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Propriedade associativa de multiplicação

Como foi feito para a soma, a propriedade associativa da multiplicação indica que:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Pode atendê -lo: soma de polinômios, como é feito, exemplos, exercícios

No caso do conjunto de números reais, é fácil verificar se é sempre. Por exemplo, usando os valores a = 2, b = 3, c = 1, você precisa::

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Os números reais atendem à propriedade associativa da soma e da multiplicação. Por outro lado, em outro conjunto, como o dos vetores, a soma é associativa, mas o produto cruzado ou o produto vetorial não é.

Aplicações da propriedade associativa de multiplicação

Uma vantagem que as operações em que a propriedade associativa é atendida é estar agrupando da maneira mais conveniente é cumprida. Isso facilita muito a resolução.

Por exemplo, suponha que em uma pequena biblioteca existem 3 prateleiras com 5 entretenimento cada. Em cada entretenimento, existem 8 livros. Quantos livros estão no total?

Podemos executar a operação da seguinte forma: Total de livros = (3 x 5) x 8 = 15 x 8 = 120 livros.

Ou assim: 3 x (5 x 8) = 3 x 40 = 120 livros.

Figura 2. Uma aplicação da propriedade associativa da multiplicação é calcular o número de livros em cada prateleira. Imagem criada por f. Zapata.

Exemplos

-Nos conjuntos de números naturais, inteiros, racionais, reais e complexos, a propriedade associativa da soma e multiplicação é cumprida.

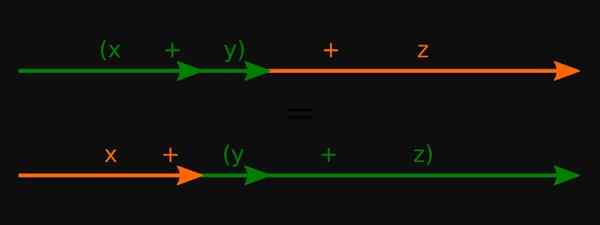Figura 3. Para números reais, a propriedade associativa da soma é cumprida. Fonte: Wikimedia Commons.

-Para polinômios que eles também se aplicam nessas operações.

-Nos casos de operações de subtração, divisão e exponenciação, a propriedade associativa não é cumprida em números reais ou polinômios.

Pode servir a você: Orthoedro: fórmulas, área, volume, diagonal, exemplos

-No caso de matrizes, a propriedade associativa é atendida para a soma e multiplicação, embora no último caso, a comutividade não seja atendida. Isso significa que, dadas as matrizes A, B e C, é verdade que:

(A x b) x c = a x (b x c)

Mas ... a x b ≠ b x a

Propriedade associativa em vetores

Os vetores formam um conjunto diferente de números reais ou números complexos. As operações definidas para o conjunto de vetores são um pouco diferentes: há soma, subtração e três tipos de produtos.

A soma dos vetores atende à propriedade associativa, bem como números, polinômios e matrizes. Quanto aos produtos escalares, subindo por vetor e cruz entre vetores, o último não se encontra, mas o produto escalar, que é outro tipo de operação entre vetores, cumpre, levando em consideração o seguinte:

-O produto de um escalar para um vetor resulta em um vetor.

-E escalando dois vetores, é um escalar.

Portanto, dados os vetores v, ou e C, E além de um escalar λ, é possível escrever:

-Soma dos vetores: v +(ou + C ) = (v + ou) + C

-Produto escalar: λ (v • ou ) = (λv) • ou

O último é possível graças ao que v • ou É um escalar e λv É um vetor.

Porém:

v × (ou × C ) ≠ (v × ou)×C

Fator Polinomial agrupando termos

Este aplicativo é muito interessante, porque, como afirmado acima, a propriedade associativa ajuda a resolver certos problemas. A soma dos monômios é associativa e isso pode ser usado para levar em consideração quando um fator comum óbvio não aparecer à primeira vista.

Pode atendê -lo: polígono convexo: definição, elementos, propriedades, exemplos

Por exemplo, suponha que seja solicitado a fator: x³ + 2x² + 3x +6. Esse polinômio não tem um fator comum, mas vamos ver o que acontece se for agrupado dessa maneira:

x³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

A primeira parêntese tem como um fator comum x²:

x³ + 2x² = x² (x+2)

No segundo, o fator comum é 3:

3x +6 = 3 (x + 2)

Então:

x³ + 2x² + 3x +6 = x²(x+ 2)+ 3 (x+ 2)

Agora há um fator comum óbvio, que é x+2:

x²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Exercícios

- Exercício 1

A construção de uma escola tem 4 andares e em cada um há 12 salas de aula com 30 mesas dentro. Quantas mesas a escola tem no total?

Solução

Este problema é resolvido aplicando a propriedade associativa da multiplicação, vamos ver:

Número total de mesas = 4 andares x 12 salas de aula /piso x 30 mesas /sala de aula = (4 x 12) x 30 mesas = 48 x 30 = 1440 mesas.

O Se preferir: 4 x (12 x 30) = 4 x 360 = 1440 mesas

- Exercício 2

Dados os polinômios:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Aplique a propriedade associativa da soma para encontrar (x) + b (x) + c (x).

Solução

Os dois primeiros podem ser agrupados e o resultado adiciona o terceiro:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Polinomial c (x) é adicionado imediatamente:

[x⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

O leitor pode verificar se o resultado é idêntico se resolvido pela opção a (x) + [b (x) + c (x)]]].

Referências

1. Jiménez, r. 2008. Álgebra. Prentice Hall.
2. A matemática é divertida. Leis comutativas, associativas e distritais. Recuperado de: Mathisfun.com.
3. Armazém de matemática. Definição de propriedade associativa. Recuperado de: Mathwarehouse.com.
4. Cienting. Propriedade associativa e comutativa de adição e multiplicação (com exemplo). Recuperado de: cienting.com.
5. Wikipedia. Propriedade associativa. Recuperado de: em.Wikipedia.org.