Programação linear para que é isso, modelos, restrições, aplicações

O programação linear É um método matemático que serve para otimizar (maximizar ou minimizar conforme necessário) uma função cujas variáveis ​​estão sujeitas a restrições, desde que a função e as restrições sejam linearmente dependentes das variáveis.

Geralmente a função de otimizar uma situação prática, como o ganho de um fabricante cujas insumos, mão -de -obra ou máquinas são limitadas.

figura 1. A programação linear é amplamente usada para otimizar os lucros. Fonte: piqsels.

Um dos casos mais simples é o de uma função linear a ser maximizada, que depende apenas de duas variáveis, chamadas Variáveis ​​de decisão. Pode ser formado:

Z = k₁x + k₂e

Com k₁ e que₂ constantes. Esta função é conhecida como Função objetiva. É claro que existem situações que merecem mais de duas variáveis ​​para seu estudo, sendo mais complexas:

Z = k₁x₁ + k₂x₂ + k₃x₃ +.. .

E restrições também são matematicamente modeladas por meio de um sistema de equações ou desigualações, igualmente lineares em x e e.

O conjunto de soluções deste sistema é chamado soluções viáveis qualquer Pontos viáveis. E entre os pontos viáveis, há pelo menos um, o que otimiza a função objetiva.

A programação linear foi desenvolvida independentemente pelo físico e matemático americano.

O método de resolução de problemas conhecido como Método simplex É a criação de Dantzig, que trabalhou para a Força Aérea dos EUA, a Universidade de Berkeley e a Universidade de Stanford.

Figura 2. Os matemáticos George Dantzig (à esquerda) e Leonid Kantorovich (direita). Fonte: f. Zapata.

[TOC]

Modelos de programação linear

Os elementos necessários para estabelecer um modelo de programação linear, apropriado a uma situação prática, são:

-Função objetiva

-Variáveis ​​de decisão

-Restrições

Na função objetiva, o que você deseja alcançar é definido. Por exemplo, suponha que se deseje maximizar os lucros obtidos da fabricação de determinados produtos. Em seguida, a função de "lucro" é estabelecida, de acordo com o preço pelo qual os produtos são vendidos.

Em termos matemáticos, essa função pode ser expressa abreviada usando o resumo:

Z = ∑k_Yo x_Yo

Nesta equação, k_Yo Eles são coeficientes e x_Yo são as variáveis ​​de decisão.

Variáveis ​​de decisão são os elementos do sistema cujo controle é e seus valores são números reais positivos. No exemplo proposto, as variáveis ​​de decisão são o valor de cada produto a ser fabricado para obter o ganho máximo.

Finalmente, temos as restrições, que são equações lineares ou desigualdades em termos de variáveis ​​de decisão. Eles descrevem as limitações para o problema, que são conhecidas e podem ser, por exemplo, as quantidades de matéria -prima disponíveis na fabricação.

Pode atendê -lo: funções superiores a dois (exemplos)

Tipos de restrições

Você pode ter uma quantidade de limitações, começando de J = 1 até J = m. Matematicamente, as restrições são de três tipos:

1. PARA_J = ∑ a_{eu j} . x_Yo
2. B_J ≥ ∑ b_{eu j} . x_Yo
3. C_J ≤ ∑ c_{eu j} . x_Yo

A primeira restrição é do tipo de equação linear e significa que o valor para_J, o que é conhecido, deve ser respeitado.

As duas restrições restantes são desigualdades lineares e significa que os valores de B_J e C_J, Conhecido, pode ser respeitado ou superado, quando o símbolo que aparece é ≥ (maior ou igual a) ou respeito ou não, se o símbolo for ≤ (menor ou igual a).

Exemplo de modelo

Os campos de aplicação são muito diversos, cobrindo da administração de empresas à nutrição, mas para entender o método, um modelo simples de uma situação prática com duas variáveis ​​é então proposto.

Uma pastelaria local é conhecida por duas especialidades: The Black Jungle Cake e The Sacrista Cake.

Em sua elaboração, eles exigem ovos e açúcar. Para a selva preta, 9 ovos e 500 g de açúcar são necessários, enquanto 8 ovos e 800 g de açúcar são necessários para a sacripenina. Os respectivos preços de venda são de US $ 8 e 10.

O problema é: quantos bolos de cada tipo se a pastelaria for?

Variáveis ​​de decisão

As variáveis ​​de decisão são "X" e "Y", que recebem valores reais:

-X: a quantidade de bolos da selva preta

-Y: bolos do tipo sacriphantino.

Restrições

As restrições são dadas pelo fato de que o número de bolos é uma quantidade positiva e há quantidades limitadas de matéria -prima para prepará -las.

Portanto, de maneira matemática, essas restrições adquirem o formulário:

1. x ≥ 0
2. e ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 e ≤ 10

Restrições 1 e 2 constituem o Condição não -negativa anteriormente expostos e todas as desigualdades levantadas são lineares. Nas restrições 3 e 4 são os valores que não devem ser superados: 144 ovos e 10 kg de açúcar.

Função objetiva

Finalmente, a função objetiva é o ganho obtido pela fabricação de “X” quantidade de bolos da selva preta mais “y” quantidade de sacristios. É construído multiplicando preço por quantidade de bolos fabricados e adicionando para cada tipo. É uma função linear que chamaremos de g (x, y):

G = 8x + 10y

Métodos de solução

Entre as várias metodologias de solução estão os métodos gráficos, o algoritmo simplex e o método do ponto interno, para mencionar alguns.

- Método gráfico ou geométrico

Quando você tem um problema de duas variáveis, como a seção anterior, as restrições determinam uma região poligonal no plano XY, chamar região viável qualquer Região de viabilidade.

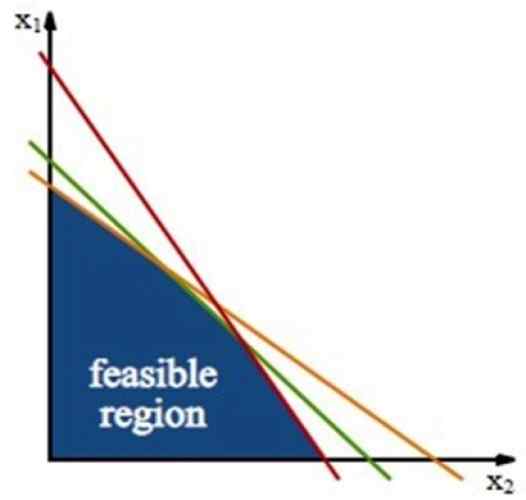Figura 3. A região viável, onde a solução do problema de otimização está localizada. Fonte: Wikimedia Commons.

Esta região é construída através Linhas de restrição, que são as linhas obtidas das desigualdades das restrições, trabalhando apenas com o sinal de igualdade.

Pode atendê -lo: conjunto finito: propriedades, exemplos, exercícios resolvidos

No caso da padaria que deseja otimizar os lucros, as linhas de restrição são:

1. x = 0
2. y = 0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Todos os pontos da região bloqueados por essas linhas são soluções possíveis, então há infinitos delas. Exceto no caso em que a região viável está vazia; nesse caso, o problema levantado carece de uma solução.

Felizmente, para o problema da pastelaria, a região viável não está vazia, nós a temos abaixo.

Figura 4. A região viável do problema da massa. A linha reta 0 cruza a origem. Fonte: f. Zapata com geogebra.

A solução ideal, se existe, é com a ajuda da função objetiva. Por exemplo, quando se trata de encontrar o ganho máximo G, você tem a seguinte linha, que é chamada Iso-benéfico reto:

G = k₁x + k₂e → y = -k₁x / k₂ + G/ k₂

Com esta linha, todos os pares (x, y) são obtidos que fornecem um dado ganho G, então há uma família de linhas de acordo com o valor de g, mas tudo com a mesma inclinação -k₁ / k₂, para que eles sejam paralelos retos.

A solução ideal

Agora, pode -se demonstrar que a solução ideal de um problema linear é sempre um extremo ou vértice da região viável. Então:

A solução de linha é a mais distante da origem e que tem pelo menos um ponto em comum com a região viável.

Se a linha mais próxima da origem tiver um segmento inteiro em comum com a região viável, diz -se que existem soluções infinitas. Este caso ocorre se a inclinação da linha ISO-Benefit for igual à de qualquer uma das outras linhas que limitam a região.

Para nossa massa, os vértices candidatos são A, B e C.

- Método Simplex de Dantzig

O método gráfico ou geométrico é aplicável a duas variáveis. No entanto, é mais complicado quando há três variáveis ​​e impossível de usar para um número maior de variáveis.

Quando se trata de problemas de mais de duas variáveis, o Método simplex, que consiste em uma série de algoritmos para otimizar funções objetivas. Matrizes e aritméticos simples são geralmente usados ​​para realizar os cálculos.

O método simplex começa escolhendo uma solução viável e verificando se for ideal. Se for, já resolvemos o problema, mas se não for, continua em direção a uma solução mais próxima da otimização. Se a solução existir, o algoritmo com ele em algumas tentativas.

Pode atendê -lo: qual é o intervalo de estatísticas? (Com exemplos)

Formulários

A programação linear e não linear aplicada em muitos campos para tomar as melhores decisões na redução de custos e no aumento dos lucros, que nem sempre são monetários, pois eles podem ser medidos no tempo, por exemplo, se você procurar minimizar o tempo necessário para realizar uma série de operações.

Aqui estão alguns campos:

-No marketing, é usado para encontrar a melhor combinação de mídia (redes sociais, televisão, imprensa e outros) para anunciar um determinado produto.

-Para a alocação de trabalho apropriada ao pessoal de uma empresa ou fábrica ou agendas para eles.

-Na seleção dos alimentos mais nutritivos e ao menor custo nas indústrias de gado e aves.

Exercícios resolvidos

- Exercício 1

Graça o modelo de programação linear criado nas seções anteriores.

Solução

É necessário representar graficamente o conjunto de valores determinados pelo sistema de restrições especificadas no problema:

1. x ≥ 0
2. e ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8 e ≤ 10

A região dada pelas desigualdades 1 e 2 corresponde ao primeiro quadrante do avião cartesiano. Quanto às desigualdades 3 e 4, começa encontrando as linhas de restrição:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y = 100

A região viável é um quadrilateral cujos vértices são pontos A, B, C e D.

O ganho mínimo é 0, portanto, a linha 8x + 10 e 10 é o limite inferior e as linhas ISO -Benefit têm pendente -8/10 = -0.8.

Este valor é diferente das inclinações das outras linhas de restrição e, como a região viável é limitada, existe a solução única.

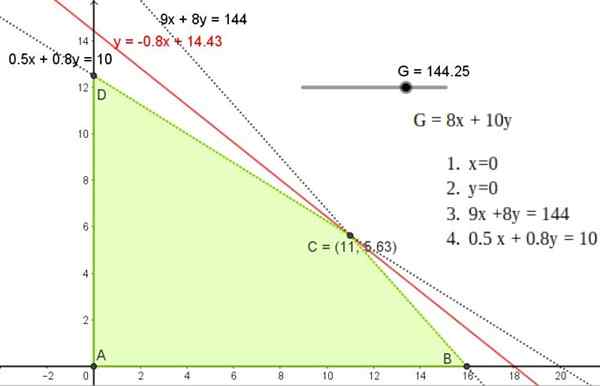Figura 5. Solução gráfica do Exercício 1, mostrando a região viável e a solução de ponto C em um dos vértices da referida região. Fonte: f. Zapata.

Esta solução corresponde a uma linha de inclinação -0.8 que passa por um dos pontos A, B ou C, cujas coordenadas são:

A (11; 5.625)

B (0; 12.5)

C (16, 0)

Solução ideal

Calculamos o valor de G para cada um desses pontos:

-(11; 5;.625): g_PARA = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): g_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): g_C = 8 x 16 + 10 x 0 = 128

O maior ganho é fabricar 11 bolos da selva preta e 5.625 bolos sacripantinos. Esta solução concorda com a encontrada através do software.

- Exercício 2

Verifique o resultado do exercício anterior usando a função Solver (Solutioner) disponível na maioria das planilhas, como Excel ou Calc De LibreOffice, que incorporam o algoritmo simplex para otimização de programação linear.

Solução

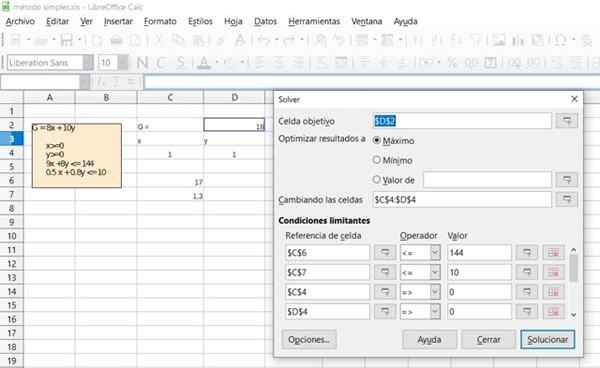Figura 6. Detalhe da solução do Exercício 1 através da Free Office Calc Stanheet. Fonte: f. Zapata. 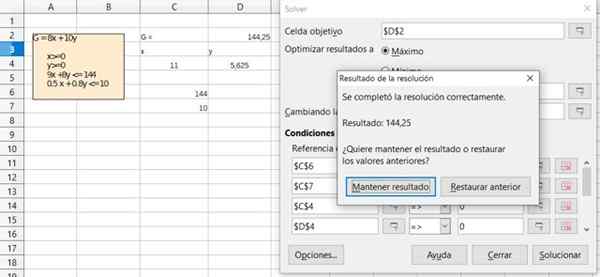Figura 7. Detalhe da solução do Exercício 1 através da Free Office Calc Stanheet. Fonte: f. Zapata.

Referências

1. Brilhante. Programação linear. Recuperado de: brilhante.org.
2. Eppen, g. 2000. Pesquisa de operações em ciências administrativas. 5 ª. Edição. Prentice Hall.
3. Haeussler, e. 1992. Matemática para Administração e Economia. 2º. Edição. Grupo Editorial Americano Ibero.
4. Hiru.EUS. Programação linear. Recuperado de: hiru.EUS.
5. Wikipedia. Programação linear. Recuperado de: é. Wikipedia.org.