Fórmula e equações de probabilidade condicional, propriedades, exemplos

O Probabilidade Condicional É a possibilidade de ocorrência de um determinado evento, uma vez que outro ocorre como uma condição. Essas informações adicionais podem modificar (ou talvez não) a percepção de que algo acontecerá.

Por exemplo, podemos nos perguntar: “Qual é a probabilidade de chover hoje, pois dois dias atrás não chove?". O evento do qual queremos saber a probabilidade é que ele chove hoje e as informações adicionais que condicionariam a resposta é que "dois dias atrás não chove".

figura 1. A probabilidade de chover hoje, pois choveu ontem também é um exemplo de probabilidade condicional. Fonte: Pixabay.

Ser um Espaço probabilístico composto de ω (espaço de amostra), ℬ (eventos aleatórios) e P (a probabilidade de cada evento), além de eventos A e B que pertencem a ℬ.

A probabilidade condicionada que ocorre, pois B, que é indicada como P (A│B), é definida dessa maneira:

P (a│b) = p (a∩b) / p (b) = p (a e b) / p (b)

Onde: p (a) é a probabilidade de ocorrência de a, p (b) é a probabilidade de evento b e é diferente de 0, e p (a∩b) é a probabilidade da interseção entre a e b, isto é ,, a probabilidade de ocorrer ambos os eventos (probabilidade conjunta).

Esta é uma expressão para o teorema de Bayes aplicado a dois eventos, proposto em 1763 pelo teólogo inglês e matemático Thomas Bayes.

[TOC]

Propriedades

-Toda a probabilidade condicional está entre 0 e 1:

0 ≤ p (a│b) ≤ 1

-A probabilidade de o evento acontecer, uma vez que este evento ocorre, é obviamente 1:

P (a│a) = p (a∩a) / p (a) = p (a) / p (a) = 1

-Se dois eventos são exclusivos, ou seja, eventos que não podem acontecer simultaneamente, a probabilidade condicional que um deles aconteça é 0, uma vez que a interseção é anulada:

P (a│b) = p (a∩b) / p (b) = 0 / p (b) = 0

-Se B é um subconjunto de A, a probabilidade condicional também é 1:

Pode atendê -lo: toroid ou Toro dona

P (b│a) = p (a∩b) / p (a) = 1

Importante

P (A│B) geralmente não é igual a P (B│a); portanto, você deve tomar cuidado para não trocar eventos ao encontrar probabilidade condicional.

Regra geral de multiplicação

Muitas vezes você deseja encontrar a probabilidade articular P (A∩b), em vez de probabilidade condicional. Então, através do teorema a seguir, você tem:

P (a∩b) = p (a e b) = p (a│b). P (b)

O teorema pode ser estendido para três eventos A, B e C:

P (a∩b∩c) = p (a e b e c) = p (a) · p (b│a) · p (c│a∩b)

E também para vários eventos, como₁, PARA₂, PARA₃ E mais, pode ser expresso da seguinte forma:

P (a₁∩ a₂ ∩ a₃… ∩ A_n) = P (A₁) . P (a₂│a₁). P (a₃│a₁∩ a₂) ... P (A_n│a₁∩ a₂∩… a_N-1)

Quando é o caso de eventos que ocorrem em sequência e através de diferentes estágios, é conveniente organizar os dados em um diagrama ou tabela. Isso facilita a visualização das opções para alcançar a probabilidade solicitada.

Exemplos disso são os diagrama de árvore e a Tabela de contingência. De um deles, você pode construir o outro.

Exemplos de probabilidade condicional

Vejamos algumas situações em que as probabilidades de um evento são alteradas pela ocorrência de outro:

- Exemplo 1

Em uma loja doce, dois tipos de bolos são vendidos: morango e chocolate. Ao registrar as preferências de 50 clientes de ambos os sexos, foram determinados os seguintes valores:

-27 mulheres, das quais 11 preferem morango e 16 bolo de chocolate.

-23 homens: 15 chocolate e 8 morango.

A probabilidade de um cliente escolher um bolo de chocolate pode ser determinado aplicando a regra de Laplace, segundo a qual a probabilidade de qualquer evento é:

P = número de eventos favoráveis/número total de eventos

Nesse caso, de 50 clientes, um total de 31 prefere chocolate, para que a probabilidade seja p = 31/50 = 0.62. Isto é, 62% dos clientes preferem bolo de chocolate.

Pode atendê -lo: equações polinomiais

Mas seria diferente se o cliente fosse uma mulher? Este é um caso de probabilidade condicional.

Tabela de contingência

Através de uma tabela de contingência como esta, os totais são facilmente visualizados:

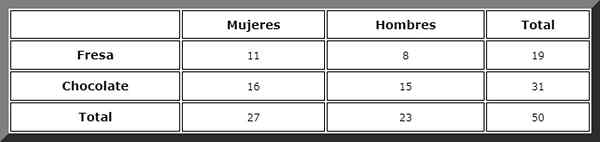
Em seguida, os casos favoráveis ​​são observados e a regra de Laplace é aplicada, mas antes de definirmos os eventos:

-B é o evento "cliente feminino".

-A é o evento "preferir bolo de chocolate" sendo uma mulher.

Vamos à coluna rotulada como "mulheres" e lá vemos que o total é 27.

Então o caso favorável é procurado na linha "chocolate". Existem 16 eventos desses, portanto, a probabilidade procurada é diretamente:

P (a│b) = 16/27 = 0.5924

A 59.24 % das mulheres preferem bolo de chocolate.

Esse valor coincide quando contrastamos com a definição inicialmente dada de probabilidade condicional:

P (a│b) = p (a∩b) / p (b)

Garantimos a nós mesmos através da regra de Laplace e os valores da tabela:

P (b) = 27/50

P (A e B) = 16/50

Onde p (a e b) é a probabilidade de o cliente preferir chocolate e ser uma mulher. Agora os valores são substituídos:

P (a│b) = p (a e b)/p (b) = (16/50)/(27/50) = 16/27 = 0.5924.

E está provado que o resultado é o mesmo.

- Exemplo 2

Neste exemplo, a regra de multiplicação se aplica. Suponha que, na exposição de uma loja, há calças em três tamanhos: pequeno, médio e grande.

Em muito com um total de 24 calças, das quais existem 8 de cada tamanho e todos são misturados. Qual seria a probabilidade de extrair dois deles e que ambos eram pequenos?

É claro que a probabilidade de extrair calças pequenas na primeira tentativa é 8/24 = 1/3. Agora, a segunda extração está condicionada ao primeiro evento, pois quando você tira calças, não há mais 24, mas 23. E se uma calça pequena for removida, existem 7 em vez de 8.

Pode servir a você: Princípio multiplicativo: Técnicas e exemplos de contagem

O evento A é para tirar uma calça pequena, tendo tomado outro na primeira tentativa. E o evento B é o de pequenas calças para o primeiro. Portanto:

P (b) = 1/3; P (a│b) = 7/24

Finalmente, através da regra de multiplicação:

P (a∩b) = (7/24).(1/3) = 7/72 = 0.097

Exercício resolvido

Em um estudo da pontualidade em voos aéreos comerciais, os seguintes dados estão disponíveis:

-P (b) = 0.83, é a probabilidade de um avião levar para levar o tempo hábil.

-P (a) = 0.81, é a probabilidade de pousar a tempo.

-P (b∩a) = 0.78 É a probabilidade de o voo chegar a tempo.

É solicitado para calcular:

a) Qual é a probabilidade de que o avião aterrisse prontamente desde que decolou a tempo?

b) A probabilidade acima é a mesma que a probabilidade de ter chegado a tempo se você conseguiu pousar prontamente?

c) e finalmente: qual é a probabilidade de chegar a hora, pois não saiu na hora?

Figura 2. A pontualidade em voos comerciais é importante, pois atrasos geram perdas milionárias. Fonte: Pixabay.

Solução para

Para responder à pergunta, é usada a definição de probabilidade condicional:

P (a│b) = p (a∩b) / p (b) = p (a e b) / p (b) = 0.78/0.83 = 0.9398

Solução b

Nesse caso, os eventos são trocados na definição:

P (b│a) = p (a∩b) / p (a) = p (a e b) / p (a) = 0.78/0.81 = 0.9630

Observe que essa probabilidade é um pouco diferente da anterior, como indicamos anteriormente.

Solução c

A probabilidade de não ser pontual é 1 - p (b) = 1 - 0,83 = 0.17, vamos chamá -lo de P (B^C), Porque é o evento complementar a levar o tempo hábil. A probabilidade condicional procurada é:

P (A│B^C) = P (a∩b^C) / P (B^C) = P (A e B^C)/P (B^C)

Por outro lado:

P (A∩B^C) = P (pouso de tempo) - P (Time Landing e Peek decolar) = 0.81-0.78 = 0.03

Nesse caso, a probabilidade procurada é:

P (A│B^C) = 0.03/0.17 = 0.1765

Referências

1. Canavos, g. 1988. Probabilidade e estatística: aplicações e métodos. McGraw Hill.
2. DeVore, j. 2012. Probabilidade e estatística para engenharia e ciência. 8º. Edição. Cengage.
3. Lipschutz, s. 1991. Série Schaum: Probabilidade. McGraw Hill.
4. Obregón, i. 1989.Teoria da probabilidade. Limusa editorial.
5. Walpole, r. 2007. Probabilidade e estatística para engenharia e ciência. Pearson.
6. Wikipedia. Probabilidade condicionada. Recuperado de: é.Wikipedia.org.