Primos relativos o que são, explicação, exemplos

Se chama primos relativos (Coprmimos ou primos em relação um ao outro) a qualquer par de números inteiros que não tenham divisor comum, exceto 1. Em outras palavras, dois números inteiros são primos relativos se, em seu colapso em números primos, eles não têm fator comum.

Por exemplo, se os 4 e 25 forem escolhidos, as decomposições em fatores primos de cada um são 2² e 5², respectivamente. Como pode ser visto, eles não têm nenhum fator comum, portanto, 4 e 25 são primos relativos.

Por outro lado, se você escolher 6 e 24, ao fazer sua quebra em fatores primos, é obtido que 6 = 2*3 e 24 = 2³*3.

Como pode ser visto, essas duas últimas expressões têm pelo menos um fator comum, portanto, eles não são primos relativos.

Características de primos relativos

Um detalhe com o qual o cuidado deve.

Por outro lado, a definição acima pode ser resumida da seguinte forma: Dois números inteiros "A" e "B" são primos relativos se, e somente, o divisor comum máximo deles é 1, ou seja, MCD (A, B ) = 1.

Duas conclusões imediatas desta definição são a que:

-Se "A" (ou "B") é um número primo, então MCD (a, B) = 1.

-Se "a" e "b" são números primos, então mcd (a, b) = 1.

Ou seja, se pelo menos um dos números escolhidos é um número primo, então o par de números são primos relativos.

Outras características

Outros resultados usados ​​para determinar se dois números são primos relativos são:

-Se dois números inteiros são consecutivos, esses são primos relativos.

-Dois números naturais "A" e "B" são primos relativos se, e somente se, os números "(2^a) -1" e "(2^b) -1" são primos relativos.

-Dois números inteiros "A" e "B" são primos relativos se, e somente se, ao representar graficamente o ponto (a, b) no plano cartesiano, e construir a linha que passa pela origem (0,0) e (a , b), isso não contém nenhum ponto com coordenadas inteiras.

Exemplos

1.- Considere números inteiros 5 e 12. As decomposições em fatores primos de ambos os números são: 5 e 2²*3, respectivamente. Em conclusão, MCD (5,12) = 1, portanto, 5 e 12 são primos relativos.

2.- Deixe os números -4 e 6. Então -4 = -2² e 6 = 2*3, de modo que o MCD (-4,6) = 2 ≠ 1. Em conclusão, -4 e 6 não são primos relativos.

Se a linha que passa pelos pares ordenados (-4,6) e (0,0), e para determinar a equação da referida linha, poderá ser verificada que isso passa pelo ponto (-2,3).

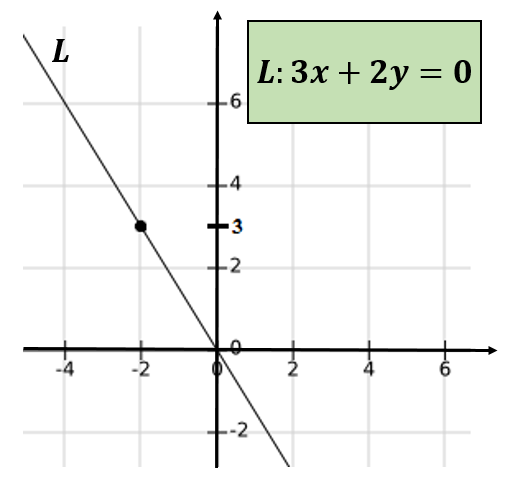
Novamente, conclui -se que -4 e 6 não são primos relativos.

3.- Os números 7 e 44 são primos relativos e podem ser concluídos rapidamente graças ao que foi dito acima, porque 7 é um número primo.

4.- Considere os números 345 e 346. Sendo dois números consecutivos, é verificado que MCD (345.346) = 1, portanto, 345 e 346 são primos relativos.

5.- Se os números 147 e 74 forem considerados, esses são primos relativos, pois 147 = 3*7² e 74 = 2*37, portanto, o MCD (147,74) = 1.

6.- Os números 4 e 9 são primos relativos. Para demonstrá -lo, você pode usar a segunda caracterização mencionada acima. De fato, 2^4 -1 = 16-1 = 15 e 2^9-1 = 512-1 = 511.

Os números obtidos são 15 e 511. As decomposições em fatores primos desses números são 3*5 e 7*73, respectivamente, de modo que o MCD (15.511) = 1.

Como você pode ver, usar a segunda caracterização é um trabalho mais longo e mais trabalhoso para verificar diretamente.

7.- Considere os números -22 e -27. Então esses números podem ser reescritos da seguinte forma: -22 = -2*11 e -27 = -3³. Portanto, o MCD (-22, -27) = 1, então -22 e -27 são primos relativos.