Explicação da condição do primeiro equilíbrio, exemplos, exercícios

O Primeira condição de equilíbrio Requer que o vetor sumptorial de todas as forças que atue em um corpo seja nulo, para que esteja em repouso (equilíbrio estático) ou com movimento retilíneo uniforme (equilíbrio dinâmico).

Essa soma das forças não é outra senão a força líquida que age no corpo, expressando esse modo matematicamente:

F_Líquido = 0

∑ F = 0

figura 1. Os construtores da antiguidade já aplicaram a primeira condição de equilíbrio, como evidenciado no monumento Stonehenge. Fonte: Pixabay.

No espaço, a primeira condição de equilíbrio gera três equações, uma para cada dimensão:

∑ f_x = 0; ∑ f_e = 0 e ∑ f_z = 0

Quando essas equações são satisfeitas, o objeto não se move ou, se isso acontecer, será com velocidade constante.

Observando ao nosso redor, percebemos que buscamos continuamente satisfazer a primeira condição de equilíbrio, para que as coisas não caam.

Portanto, procura compensar a atração gravitacional da Terra através do apoio, cordas ou apoios de alguns, para que as coisas permaneçam no lugar e não vão ao chão.

Outras vezes, o que é necessário é impedir que os campos eletromagnéticos externos interfiram na operação de circuitos elétricos e dispositivos de comunicação. Nesse caso, são as cargas elétricas que devem estar em equilíbrio.

[TOC]

Exemplos

Um grande número de objetos cotidianos satisfaz a primeira condição de equilíbrio, é uma questão de observar cuidadosamente:

Edifícios

Os construtores buscam estabilidade em construções para que os usuários fiquem seguros. O objetivo da estática é estudar as condições para equilíbrio estático em edifícios, pontes, estradas e todos os tipos de estruturas.

Higéforas e avisos de suspensão

Esses dispositivos de sinalização devem permanecer fixos para cumprir suas funções; portanto, estão sujeitos a cabos, postes e hastes de tal maneira que a primeira condição de equilíbrio seja atendida.

Pode servir a você: Terceira Lei da Termodinâmica: Fórmulas, Equações, ExemplosFigura 2. Os semáforos e os avisos de suspensão estão sujeitos de tal maneira que satisfaz a primeira condição de equilíbrio. Fonte: Pxfuel.

Drivers de balanço de eletrostesPentil

Quando materiais condutores, como cobre e outros metais, adquirem carga elétrica, o equilíbrio eletrostático é estabelecido em breve, deixando o excedente de carga na superfície condutora. Dentro do campo elétrico é zero.

Esse efeito é freqüentemente usado para isolar equipamentos elétricos e eletrônicos dos campos externos, por meio da gaiola de Faraday, de forma assim chamada. A gaiola é feita de material condutor e envolve o equipamento a ser protegido.

Durante as tempestades, os carros servem como gaiolas de faraday protegendo os ocupantes de choques elétricos.

Lâmpadas de teto

Nos sistemas de iluminação, como lâmpadas penduradas, a condição de primeiro equilíbrio é usada para consertá -las no telhado, no chão ou na parede.

Figura 3. A elaborada lâmpada de telhado chamada "aranhas" satisfaz a primeira condição de equilíbrio. Fonte: Pixabay.

Livros e objetos em mesas

Os objetos colocados em mesas e prateleiras atendem à primeira condição de equilíbrio. A força normal que o suporte exerce sobre os objetos é responsável por compensar o peso.

Medida da viscosidade de um líquido

Para determinar a viscosidade de um líquido, um objeto esférico, de diâmetro conhecido, que verá sua velocidade devido à resistência cair dentro. A velocidade da esfera é constante, estando em equilíbrio dinâmico.

Uma maior viscosidade do líquido, menos a velocidade com que a esfera se move para dentro.

Etapas para aplicar a primeira condição de equilíbrio

-Faça um diagrama de corpo livre, que mostra todas as forças que agem no corpo (omite o que o corpo exerce sobre os outros).

Pode atendê -lo: Física na Idade Média

-Selecione um sistema de coordenadas cartesianas, garantindo que, se possível, as forças estejam localizadas em qualquer um dos eixos. O endereço positivo é geralmente tomado no sentido de movimento ou em um possível movimento.

-Determine os componentes cartesianos de cada força.

-Aplique a segunda lei de Newton para cada componente, conforme estabelecido no início, há um sistema de equações.

-Resolva o sistema de equações levantadas na etapa anterior.

Exercícios resolvidos

- Exercício resolvido 1

O bloco da figura, de massa m, Se move ladeira abaixo no plano ângulo θ com velocidade constante. Calcule o valor do coeficiente de atrito cinético μ_k, Se a massa do bloco for m = 5 kg e θ = 37º.

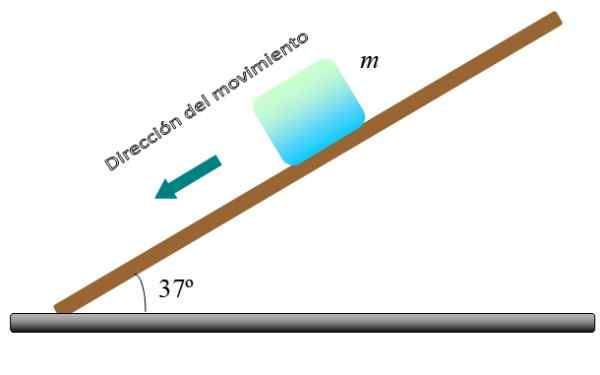Figura 4. Um bloco desliza em velocidade constante em um plano inclinado. Fonte: f. Zapata.

Solução

O primeiro passo é desenhar o diagrama do corpo livre e escolher um sistema de coordenadas cartesianas para expressar cada vetor de força. As forças que atuam no quarteirão são:

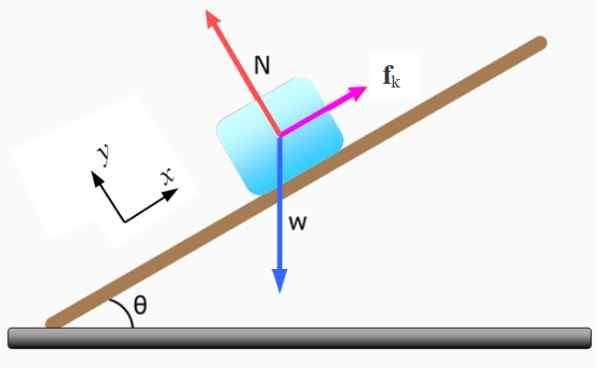Figura 5. Diagrama do corpo livre para bloco. Fonte: f. Zapata.

-O normal N Exerorado pelo plano inclinado, é perpendicular à superfície deste.

-O peso C É direcionado verticalmente para baixo.

-Fricção cinética F_k que se opõe a movimento. Se não existisse, o corpo se moveria ladeira abaixo com uma aceleração igual a g.Senθ.

Como peso C É inclinado em relação aos eixos de coordenadas selecionados, deve ser dividido em seus componentes cartesianos:

C_x = mg.Sen 37º = 5 kg x 9,8 m/s² x sin 37º = 29. 5 n
C_e = mg.cos 37º = 5 kg x 9,8 m/s² x cos 37º = 39.1 n

A segunda lei de Newton agora está aplicada, correspondendo a cada soma a 0, já que o bloco não tem aceleração ao se mover com velocidade constante:

∑ f_e = N - w_e = 0
∑ f_x = W_x - F_k = 0

A magnitude do atrito cinético é proporcional à magnitude do normal, sendo o coeficiente de atrito cinético μ_k A proporcionalidade constante.

Pode servir a você: pressão absoluta: fórmula, como é calculado, exemplos, exercícios

F_k = μ_k N

Na sua vez:

N = w_e = 39.1 n

E também:

F_k = W_x

Portanto:

29. 5 n = μ_k X 39.1 n

μ_k = 29. 5/39.1 = 0.75

- Exercício resolvido 2

Calcule a magnitude das tensões que suportam o semáforo de massa 33 kg, mostrado na figura:

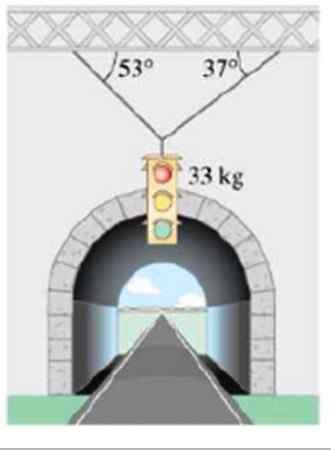Figura 6. Um semáforo está pendurado usando cabos. Fonte: Giancoli. Física com aplicações.

Solução

O diagrama do corpo livre é feito tanto para o semáforo quanto para o nó que segura os cabos:

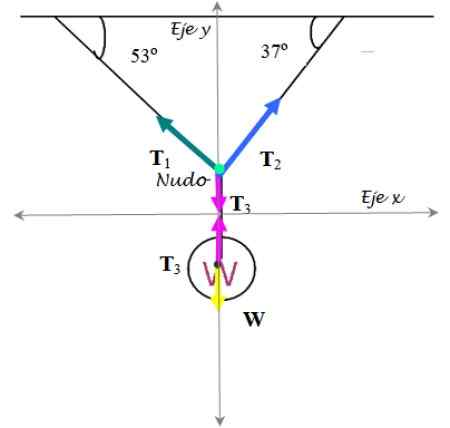Figura 7. Diagrama do corpo livre para o exercício resolvido 2. Fonte: f. Zapata.

Semáforo

Sobre o ato: a tensão t₃ para cima e peso W Down. Portanto:

∑ f_e = W - T₃ = 0

Portanto:

T₃ = 33 kg x 9.8 m/s² = 323.4 n

Nó

As tensões quebram em seus componentes cartesianos:

∑ f_e = T₁ Sen 53º + t₂ Sen 37º - T₃ = 0
∑ f_x = T₂ Cos 37º - T₁ Cos 53º = 0

E o seguinte sistema de equações lineares com duas incógnitas são obtidas₁  e T₂ :

- 0.6 t₁ + 0.8 t₂ = 0
0.8 t₁ + 0.6 t₂ = 323.4

A solução deste sistema de equações é: t₁ = 258.7 n e t₂ = 194.0 n

Assuntos de interesse

Condições de equilíbrio.

Segunda condição de equilíbrio.

Referências

1. Bedford, 2000. PARA. Mecânica para engenharia: estático. Addison Wesley.
2. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 4. Sistemas de partículas. Editado por Douglas Figueroa (USB).
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Física da Universidade com Física Moderna. 14º. Ed. Volume 1.
5. Wikipedia. Estático (mecânico). Recuperado de: é.Wikipedia.org.