Energia mecânica o que é, aplicações, exemplos

O Poder mecânico É o ritmo ao qual o trabalho é feito, que é expresso de maneira matemática para a quantidade de trabalho realizado por unidade de tempo. E como o trabalho é realizado às custas da energia absorvida, ele também pode ser elevado como energia por unidade de tempo.

Chamando P para poder, C ao trabalho, E para energia e t Ao mesmo tempo, todas as opções acima podem ser resumidas no manuseio de expressões matemáticas facilmente:

figura 1. O Gossamer Albatross, o "Flying Bicycle", atravessou o canal de La Mancha no final da década de 1970, usando apenas o poder humano. Fonte: Wikimedia Commons. Gossamer Albatross. Guroadrunner na Wikipedia inglesa [domínio público]

O bem:

As unidades de energia no sistema internacional (SI), que é o sistema de unidades universalmente adotadas, são o joule/segundo ou watt, que é abreviado w. Foi assim nomeado em homenagem ao engenheiro escocês James Watt (1736-1819), conhecido por ter criado o motor a vapor com um condensador, invenção que iniciou a revolução industrial.

Outras unidades de energia usadas nas indústrias são HP (Poder de cavalo ou cavalo de força) e o CV (cavalo a vapor). A origem dessas unidades também remonta a James Watt e à Revolução Industrial, quando o padrão de medição era o ritmo com o qual um cavalo em direção ao trabalho.

Tanto o HP quanto o CV são equivalentes a aproximadamente ¾ de quilo-w ainda sendo usado muito, especialmente em engenharia mecânica, por exemplo, na designação de motores.

Os múltiplos de Watt, como o quilo-W-W = 1000 w mencionados acima, também são frequentemente usados ​​em eletricidade. É porque o joule é uma unidade relativamente pequena de energia. O sistema britânico usa Libra-Pie/Second.

[TOC]

O que são aplicações de indústria e energia

O conceito de energia é aplicável a todos os tipos de energia, seja mecânica, elétrica, química, vento, sonônica ou qualquer tipo. O tempo é muito importante no setor, porque os processos devem ser executados o mais rápido possível.

Qualquer motor fará o trabalho necessário para ter tempo suficiente, mas o importante é fazê -lo no menor tempo possível, para aumentar a eficiência.

Uma aplicação muito simples é descrita imediatamente para esclarecer a distinção entre trabalho e poder bem.

Suponha que um objeto pesado seja interrompido por uma corda. Para fazer isso, um agente externo que faz o trabalho necessário é necessário. Digamos que este agente transfere 90 J de energia para o sistema de corpo de objetos, para que seja acionado por 10 segundos.

Pode atendê -lo: Cross Wave

Nesse caso, a taxa de transferência de energia é de 90 J/10 s ou 9 J/S. Então podemos afirmar que esse agente, uma pessoa ou um motor tem uma potência de saída de 9 W.

Se outro agente externo for capaz de alcançar o mesmo deslocamento, em menos tempo ou transferir menos energia, será capaz de desenvolver maior poder.

Outro exemplo: suponha uma transferência de energia de 90 J, que consegue mover o sistema por 4 segundos. A potência de saída será 22.5 w.

Desempenho da máquina

O poder está intimamente relacionado ao desempenho. A energia que é fornecida a uma máquina nunca é completamente transformada em trabalho útil. Uma parte importante é geralmente dissipada no calor, o que depende de muitos fatores, por exemplo, o design da máquina.

É por isso que é importante conhecer o desempenho das máquinas, que é definido como a proporção entre o trabalho entregue e a energia fornecida:

η = trabalho entregue pela máquina/energia fornecida

Onde as letras gregas η Indica o desempenho, uma quantidade adicional que é sempre menor que 1. Se você também multiplicar por 100, você tem o desempenho em termos percentuais.

Exemplos

- Seres e animais humanos desenvolvem poder durante a locomoção. Por exemplo, ao subir escadas, é necessário trabalhar contra a gravidade. Comparando duas pessoas subindo uma escada, que sobe todas as etapas primeiro, terá desenvolvido mais poder do que o outro, mas ambos fizeram o mesmo trabalho.

- Aparelhos e máquinas são especificados sua potência de saída. Uma lâmpada incandescente apropriada para iluminar um poço de sala tem uma potência de 100 W. Isso significa que a lâmpada transforma a eletricidade em luz e calor (a maioria) a uma taxa de 100 J/s.

- O motor de uma poda de grama pode consumir cerca de 250 W e o de um carro está na ordem dos 70 kW.

- Um suprimento de bomba de água caseira geralmente 0.5 hp.

- O sol gera 3.6 x 10 ²⁶ W Power.

Poder e velocidade

O poder instantâneo é obtido por um tempo infinitesimal: P = Dw/dt. A força produzida pelo trabalho causal do pequeno deslocamento infinitesimal dx é F (ambos são vetores), portanto dw = F ● dx. Substituir tudo na expressão por poder, permanece:

Pode servir a você: Força Centrifugal: Fórmulas, como é calculado, exemplos, exercícios

Portanto, o poder também pode ser expresso como o produto escalar entre força e velocidade.

Poder humano

As pessoas são capazes de gerar poderes de cerca de 1500 W ou 2 cavalos de potência, pelo menos por um curto período de tempo, como pesos pesos.

Em média, a potência diária (8 horas) é 0.1 hp por pessoa. Muito dos quais se traduz em calor, mais ou menos a mesma quantidade gerada por uma lâmpada incandescente de 75 W.

Um atleta em treinamento pode gerar em média 0.5 HP equivalente a aproximadamente 350 J/s, transformando energia química (glicose e gordura) em energia mecânica.

Figura 2. Um atleta desenvolve uma potência média de 2 hp. Fonte: Pixabay.

Quando se trata de poder humano, geralmente é preferido. A equivalência necessária é:

1 quilocaloria = 1 caloria nutricional = 4186 J

Um poder de 0.5 HP parece uma quantidade muito pequena, e é para muitas aplicações.

No entanto, em 1979, uma bicicleta impulsionada por humanos foi criada que poderia voar. Paul Maccready projetou o Gossamer Albatross, que cruzou o canal La Mancha, gerando 190 W de saída média (Figura 1).

Distribuição de energia elétrica

Uma aplicação importante é a distribuição de eletricidade entre os usuários. Empresas que fornecem lei de eletricidade a energia consumida, não a taxa na qual é consumida. É por isso que aqueles que lêem sua fatura cuidadosamente encontrarão uma unidade muito específica: o Kilowatt-Hora ou KW-H.

No entanto, quando o nome de Watt está incluído nesta unidade refere -se à energia e não ao poder.

O Kilowatt-Hora é usado para indicar o consumo de eletricidade, já que o joule, como mencionado anteriormente, é uma unidade bastante pequena: 1 watt-hora ou w-h É o trabalho realizado em 1 hora através de uma potência de 1 watt.

Portanto 1 KW-H É o trabalho que é feito em uma hora trabalhando com uma potência de 1kW ou 1000 w. Vamos colocar os números para passar esses valores para Joules:

1 w-h = 1 W x 3600 s = 3600 j

1 kw-h = 1000 w x 3600 s = 3.6 x 10 ⁶ J

Estima-se que em uma casa cerca de 200 kW-hora possa ser consumida por mês.

Pode servir a você: pressão absoluta: fórmula, como é calculado, exemplos, exercícios

Exercícios

Exercício 1

Um agricultor usa um trator para puxar um feno PACA de M = 150 kg em um plano inclinado a 15 ° e levá -lo ao celeiro, a uma velocidade constante de 5.0 km / h. O coeficiente de atrito cinético entre o feno Fardo e a rampa é 0.Quatro cinco. Encontre a potência de saída do trator.

Solução

Para esse problema, é necessário desenhar um diagrama de corpo livre para o feno Fardo que sobe no plano inclinado. Ser F A força que aplica o trator para subir o bundo, α = 15º é o ângulo de inclinação.

Além disso, a força de atrito cinética está envolvida F_tocar que se opõe ao movimento, mais o normal N e o peso C (Não confunda o w de peso com o do trabalho).

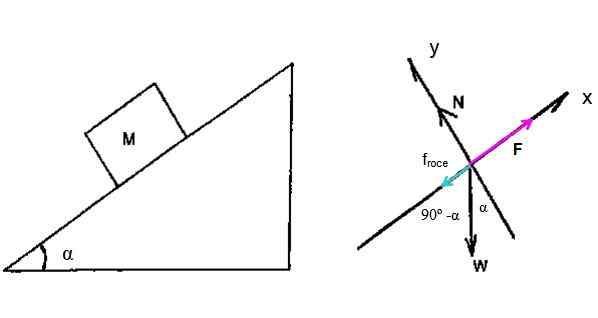Figura 3. Diagrama corporal isolado Heo Fardo. Fonte: f. Zapata.

A segunda lei de Newton oferece as seguintes equações:

∑ fx = f -w_x -F_tocar = 0 (Desde que o Bundo sobe em velocidade constante)

∑fy = n - w_e = 0 (Não há movimento ao longo do eixo x)

O atrito cinético é calculado por:

F_tocar = Coeficiente de atrito cinético x magnitude do normal

F_tocar = 0.Quatro cinco . Wy = 0.45 x 150 kg x9.8 m/s2 x cos 15º = 639 n

F = w_x + F_tocar = M.g. sin α = 150 kg. 9.8 m/s² . sin 15 º + 639 n =  1019.42 n

A velocidade e a força têm a mesma direção e significado, portanto:

P = F ● v = F. v

É necessário para transformar as unidades de velocidade:

v = 5.0 km/ h = 1.39 m/ s

Substituindo valores, você finalmente obtém:

P = 1019.42 n x 1.39 m/ s = 1417 w = 1.4 KW

Exercício 2

O motor mostrado na figura fará o upload do bloco de 2 kg, começando de repouso, com uma aceleração de 2 m/s² e em 2 segundos.

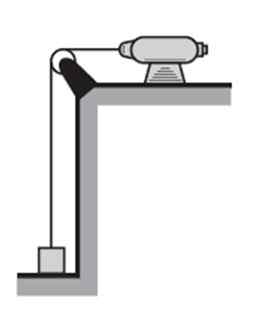Figura 4. Um motor eleva um objeto a uma certa altura, para a qual é necessário fazer o trabalho e desenvolver energia. Fonte: f. Zapata.

Calcular:

a) A altura atingida pelo bloco naquele momento.

b) o poder que o motor deve desenvolver para alcançá -lo.

Solução

a) É um movimento retilíneo uniformemente variado, portanto as equações correspondentes serão usadas, com velocidade inicial 0. A altura alcançada é dada por:

y = ½ em² = ½ . 2 m/s² . (2 s)² = 4 m.

b) Para encontrar o poder desenvolvido pelo mecanismo, a equação pode ser usada:

P = δCom δt

E como a força exercida no bloco é através da tensão na corda, que é constante em magnitude:

P = (ma).e/δT = 2 kg x 2 m/s² x 4 m / 2 s = 8 w

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dinâmico. Editado por Douglas Figueroa (USB).
2. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia.  Pearson.
3. Física Librettexts. Poder. Recuperado de: Phys.Librettexts.org
4. O livro de hipertexto da física. Poder. Recuperado de: física.Informações.
5. Trabalho, energia e poder. Recuperado de: NCERT.Nic.em