Paralelepípedo

Os paralelepípedes são figuras geométricas de seis, onde os opostos são paralelos entre si. Exemplo: um tijolo, uma caixa de sapatos, um balde, etc.

O que é um paralelepiped?

A paralelepípedo É um corpo geométrico formado por seis faces, cuja característica principal é que todos os seus rostos são paralelogramas e também suas faces opostas são paralelas entre si. É um poliedro comum em nossas vidas diárias, pois podemos encontrá -lo em caixas de sapatos, a forma de um tijolo, a forma de um microondas, etc.

Sendo um poliedro, o paralelepípedo contém um volume finito e todos os seus rostos são planos. Faz parte do grupo de prismas, que são aqueles poliedros nos quais todos os seus vértices estão contidos em dois aviões paralelos.

Elementos do paralelepírio

Rostos

Eles são cada uma das regiões formadas por paralelogramas que limitam o paralelepipe. Um paralelepípedo tem seis faces, onde cada face tem quatro rostos adjacentes e um oposto. Além disso, cada face é paralela ao seu oposto.

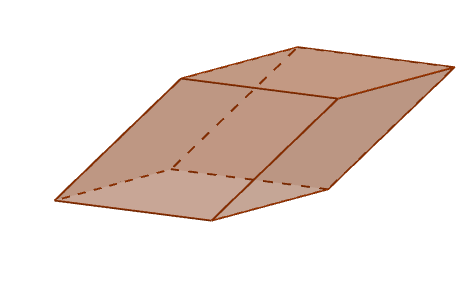Perspectiva de um paralelepírio

Arestas

Eles são o lado comum de duas faces. No total, um paralelepípedo tem doze arestas.

Vértice

É o ponto comum de três faces adjacentes dois a dois. Um paralelepípedo tem oito vértices.

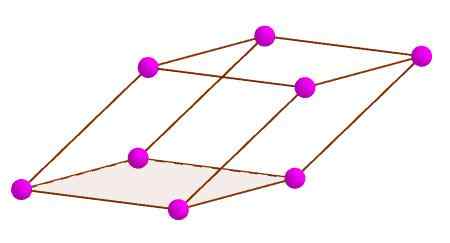Vértices de um paralelepiped

Diagonal

Dadas duas faces de um oposto paralelepírio um ao outro, podemos desenhar um segmento de linha que vai do vértice de um rosto para o vértice oposto do outro.

Este segmento é conhecido como a diagonal paralelepípeira. Cada paralelepípedo tem quatro diagonais.

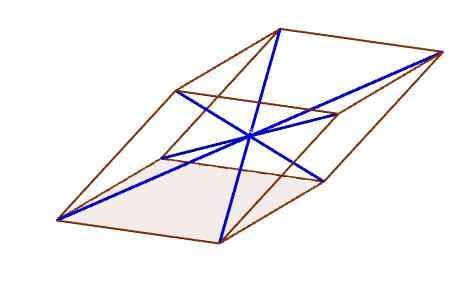Diagonais de um paralelepírio

Centro

É o ponto em que todas as diagonais se cruzam.

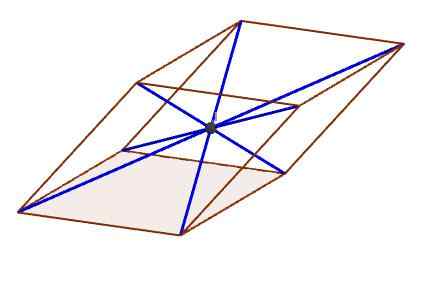O ponto da figura indica o centro, onde todas as diagonais se cruzam

Características do paralelepipe

Como já mencionamos, este corpo geométrico tem doze arestas, seis faces e oito vértices.

Em um paralelepípedo, três conjuntos formados por quatro arestas podem ser identificados, que são paralelos entre si. Além disso, as bordas desses conjuntos também estão em conformidade com a propriedade de ter o mesmo comprimento.

Características do paralelepipe

Outra propriedade representava.

Além disso, os paralelepípedes, sendo poliedros convexos, cumprem o teorema de Euler para poliedros, o que nos dá uma relação entre o número de faces, o número de arestas e o número de vértices. Esta relação é dada na forma da seguinte equação:

C + V = A + 2

Este recurso é conhecido como característica de Euler. Onde C é o número de rostos, e o número de vértices e o número de arestas.

Tipos de paralleepípedos

Podemos classificar os paralelepípedos com base em seus rostos, nos seguintes tipos:

Orthoedro

Eles são os paralelepípedos onde seus rostos são compostos por seis retângulos. Cada retângulo é perpendicular com aqueles com os quais compartilha borda. Eles são os mais comuns em nossas vidas diárias, sendo esta a forma usual de sapatos e caixas de tijolos.

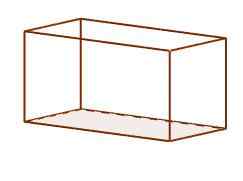Orthoedro paralelepiped

Cubo regular ou hexaedro

Este é um caso particular do anterior, onde cada um dos rostos é um quadrado.

Pode atendê -lo: elipseCubo regular ou hexaedro

O cubo também faz parte dos corpos geométricos chamados sólidos platônicos. Um sólido platônico é um poliedro convexo, de modo que tanto seus rostos quanto seus ângulos internos são iguais um ao outro.

Romboedro

É um paralelepípedo que tem um Rhombus. Esses Rhombus são todos iguais um ao outro, pois compartilham bordas.

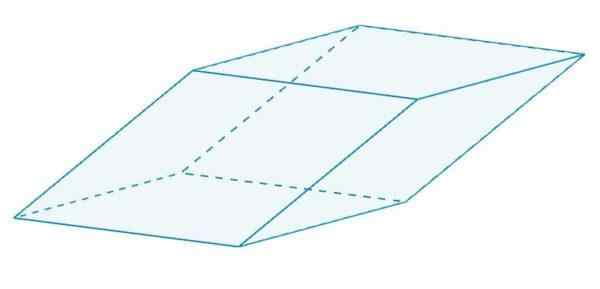Um romboedro

Romboiedro

Seus seis rostos são romboides. Lembre -se de que um romboide é um polígono de quatro e quatro ângulos que são iguais dois a dois. Os romboides são os paralelogramas que não são quadrados, nem retângulos, nem rhombus.

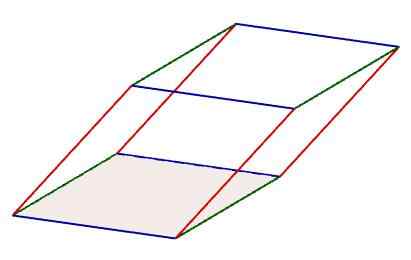
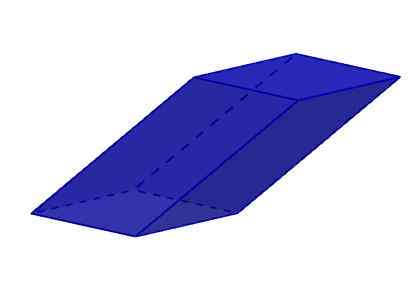Romboiedro

Por outro lado, os paralelepípedes oblíquos são aqueles em que pelo menos uma altura não corresponde à sua borda. Nesta classificação, podemos incluir rhomboedros e rhomboiedros.

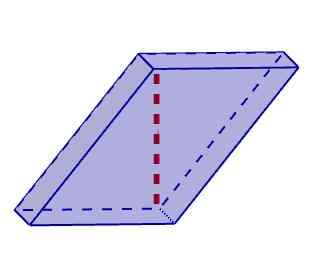Oblíquo paralelepípedo

Cálculo diagonal

Para calcular a diagonal de um ortoedro, podemos usar o teorema de Pitágoras para r para r³.

Lembre -se de que um ortoedro tem a característica de que cada lado é perpendicular com os lados que compartilham a borda. De fato, podemos deduzir que cada borda é perpendicular com aqueles que compartilham o vértice.

Para calcular o comprimento de uma diagonal de um ortoedro, procedemos da seguinte maneira:

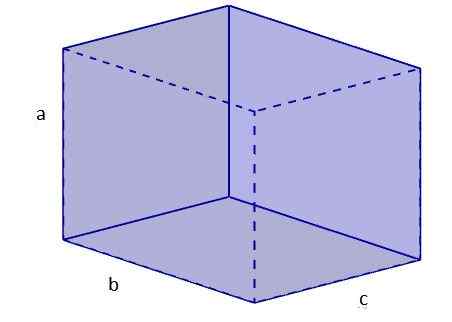
1. Calculamos a diagonal de um dos rostos, que colocaremos pela base. Para isso, usamos o teorema de Pitágoras. Vamos nomear essa diagonal d_b.

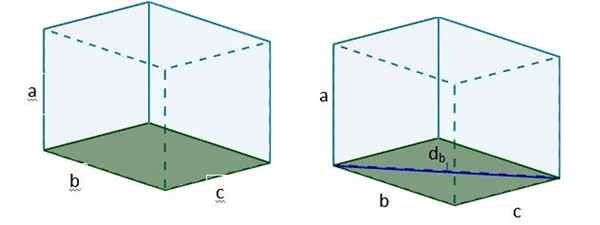
2. Então com d_b Podemos formar um novo triângulo retângulo, de modo que a hipotenusa deste triângulo seja a diagonal D buscada.

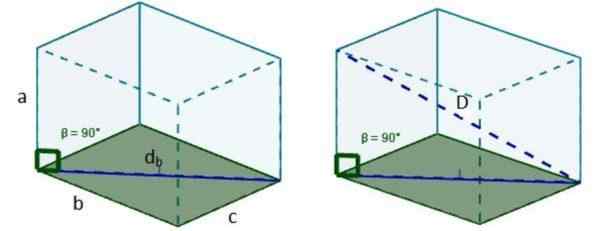
3. Usamos o teorema de Pitágoras novamente e temos que a duração dessa diagonal é:

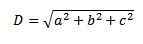
Outra maneira de calcular a diagonal de uma maneira mais gráfica é com a soma dos vetores livres.

Lembre -se de que dois vetores livres A e B são adicionados colocando a cauda do vetor B com a ponta do vetor a.

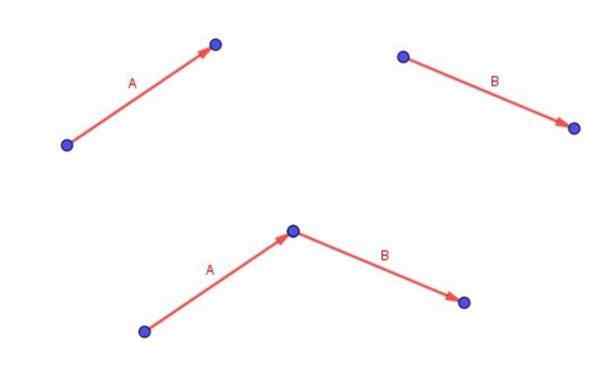
O vetor (a + b) é o que começa na cauda de A e termina na ponta de B.

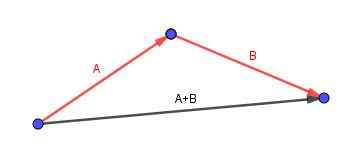
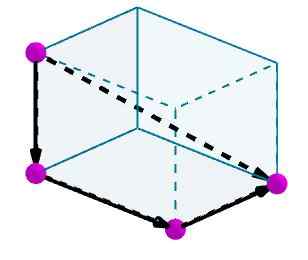
Considere um paralelepípedo ao qual queremos calcular uma diagonal. Identificamos as bordas com vetores orientados convenientes.

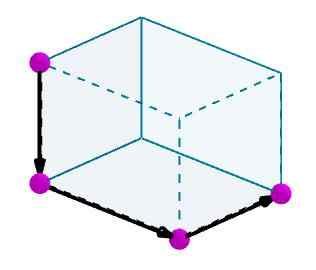
Em seguida, adicionamos esses vetores e o vetor resultante será a diagonal do paralelepípede.

Área de um paralelepiped

A área de um paralelepípede é dada pela soma de cada uma das áreas de seus rostos.

Se determinarmos um dos lados como a base,

PARA_eu + 2º_B = Área total

Para onde_eu É igual à soma das áreas de todos os lados adjacentes à base, chamada de área lateral e a_B É a área base.

Dependendo do tipo de paralelepípedo com o qual estamos trabalhando, podemos reescrever a fórmula.

Área de um ortoedro

É dado pela fórmula

A = 2 (ab + bc + ca).

Exemplo 1

Dado o seguinte ortoedro, com os lados a = 6 cm, b = 8 cm e c = 10 cm, calcule a área paralelepipe e o comprimento de sua diagonal.

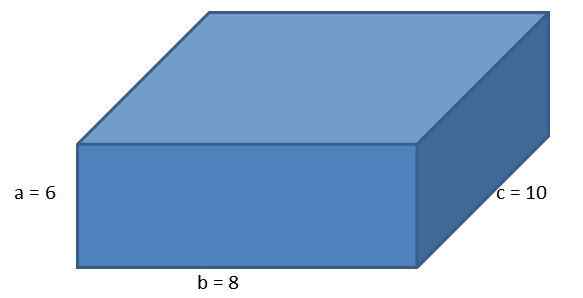
Usando a fórmula para a área de um ortoedro, temos que

A = 2 [(6) (8) + (8) (10) + (10) (6)] = 2 [48 + 80 + 60] = 2 [188] = 376 cm².

Observe que como um ortoedro é o comprimento de qualquer um de seus quatro diagonais é o mesmo.

Pode servir a você: Integral indefinido: propriedades, aplicações, cálculo (exemplos)

Usando o teorema de Pitágoras para o espaço, temos que

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Área do cubo

Como cada borda tem o mesmo comprimento, temos que A = B e A = C. Substituindo na fórmula anterior que temos

A = 2 (aa + aa + aa) = 2 (3a²) = 6a²

A = 6a²

Exemplo 2

A caixa de um console de jogo tem a forma de um cubo. Se queremos embrulhar esta caixa com papel de presente, quanto papel gastaríamos sabendo que a duração das bordas do cubo é de 45 cm?

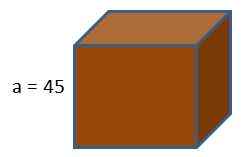
Usando a fórmula da área do cubo, conseguimos isso

A = 6 (45 cm)² = 6 (2025 cm²) = 12150 cm²

Área de um rhomboedro

Como todos os seus rostos são iguais, é suficiente calcular a área de um deles e multiplique por seis.

Temos que a área de um rombus pode ser calculada por suas diagonais com a seguinte fórmula

PARA_R = (Dd)/2

Usando esta fórmula, segue -se que a área total do rhomboedro é

PARA_T = 6 (dd)/2 = 3dd.

Exemplo 3

Os rostos do próximo rhomboedro são formados por um rombus cuja diagonal é d = 7 cm e d = 4 cm. Sua área será

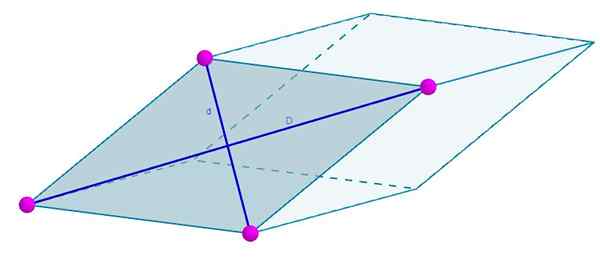
A = 3 (7 cm) (4 cm) = 84 cm².

Área de um rhomboiedro

Para calcular a área de um rhomboiedro, devemos calcular a área dos romboides que a compõem. Como os paralelepípedes cumprem a propriedade que os lados opostos têm a mesma área, podemos associar os lados em três pares.

Dessa forma, temos que sua área será

PARA_T = 2b₁h₁ + 2b₂h₂ + 2b₃h₃

Onde b_Yo são as bases associadas aos lados e H_Yo sua altura relativa correspondente às referidas bases.

Exemplo 4

Considere o seguinte paralelepiped,

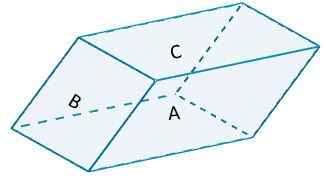
onde o lado a e o lado a '(o lado oposto) são baseados b = 10 e por altura h = 6. A área marcada terá um valor de

PARA₁ = 2 (10) (6) = 120

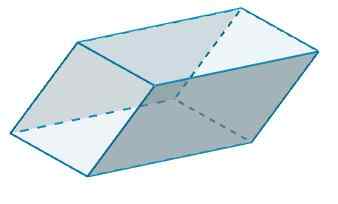
B e B 'têm B = 4 e H = 6, então

PARA₂ = 2 (4) (6) = 48

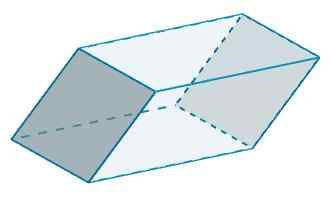
E C e C 'têm B = 10 e H = 5 também

PARA₃ = 2 (10) (5) = 100

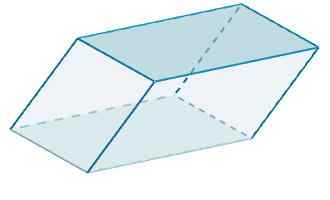
Finalmente a área de Rhomboiedro é

A = 120 + 48 + 100 = 268.

Volume de um paralelepiped

A fórmula que nos dá o volume de um paralelepírio é o produto da área de um de seus rostos devido à altura correspondente à referida face.

V = a_Ch_C

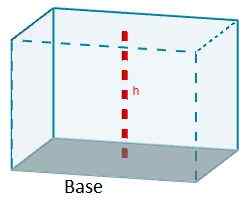
Dependendo do tipo de paralelepípede, esta fórmula pode ser simplificada.

Assim, temos, por exemplo, que o volume de um ortoedro seria dado por

V = abc.

Onde a, b e c representam o comprimento das bordas ortoedro.

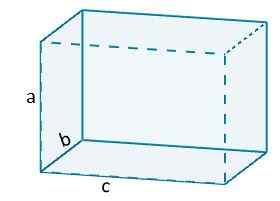
E no caso particular do cubo é

V = a³

Exemplo 1

Existem três modelos diferentes para caixas de biscoitos e você quer.

O primeiro é um cubo cuja borda tem um comprimento de A = 10 cm.

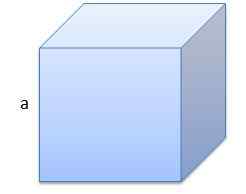
Seu volume será V = 1000 cm³

O segundo é B = 17 cm, C = 5 cm, D = 9 cm.

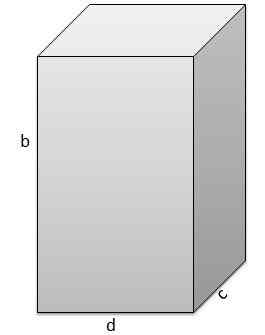
E, portanto, seu volume é v = 765 cm³

E o terceiro tem E = 9 cm, F = 9 cm e G = 13 cm.

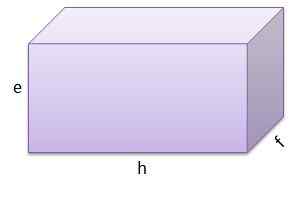
E seu volume é v = 1053 cm³

Pode atendê -lo: tipos de ângulos, características e exemplos

Portanto, a caixa com o maior volume é o terceiro.

Outro método para obter o volume de um paralelepípede é recorrer à álgebra vetorial. Em particular, o produto escalar triplo.

Uma das interpretações geométricas do produto triplo escalar é o do volume do paralelepipe, cujas bordas são três vetores que compartilham o mesmo vértice que um ponto de partida.

Dessa forma, se tivermos um paralelepípedo e queremos saber qual é o seu volume, é suficiente para representá -lo em um sistema de coordenadas em r³ coincidindo um de seus vértices com a origem.

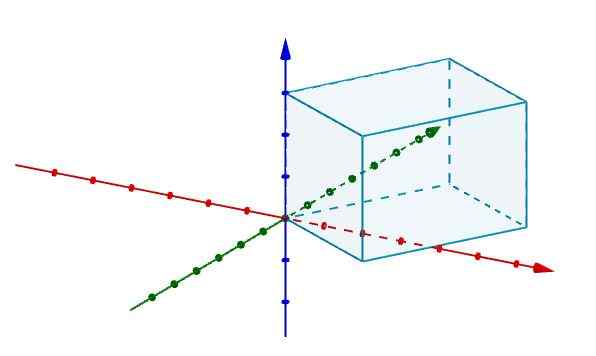
Em seguida, representamos as bordas que concordam na origem com os vetores, como mostrado na figura.

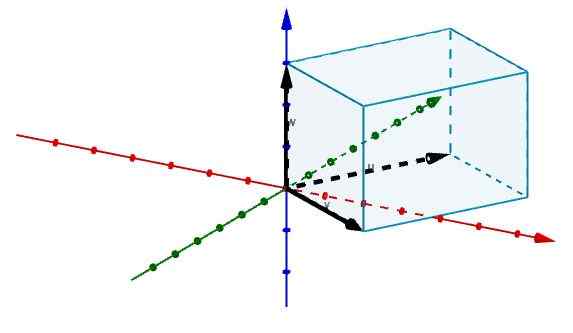
E dessa forma temos que o volume do referido paralelepipe é dado por

V = | AXB ∙ C |

Ou equivalente, o volume é o determinante da matriz 3 × 3, formada pelos componentes dos vetores da borda.

Exemplo 2

Representando o seguinte paralelepipe em r³ Podemos ver que os vetores que determinam são os seguintes

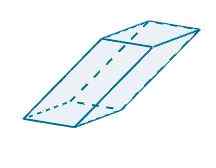
u = (-1, -3,0), v = (5, 0, 0) e w = (-0.25, -4, 4)

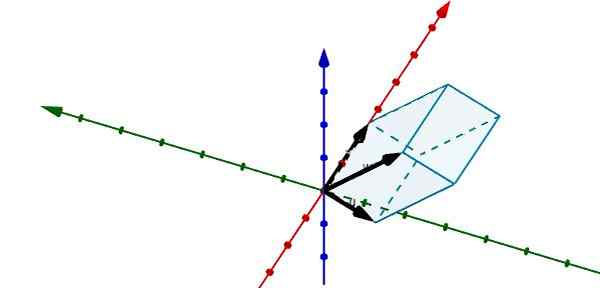
Usando o produto escalar triplo que temos

V = | (UXV) ∙ W |

Uxv = (-1, -3.0) x (5, 0, 0) = (0,0, -15)

(UXV) ∙ W = (0,0,- 15) ∙ (-0.25, -4, 4) = 0 + 0 + 4 ( - 15) = - 60

Isso conclui que v = 60

Considere agora o seguinte paralelepiped em r³ cujas bordas são determinadas pelos vetores

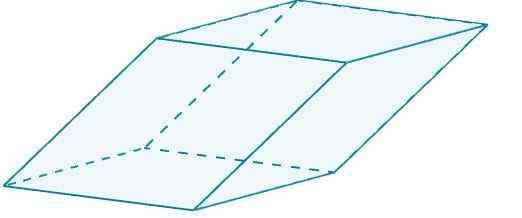
A = (2, 5, 0), b = (6, 1, 0) e c = (3, 4, 4)

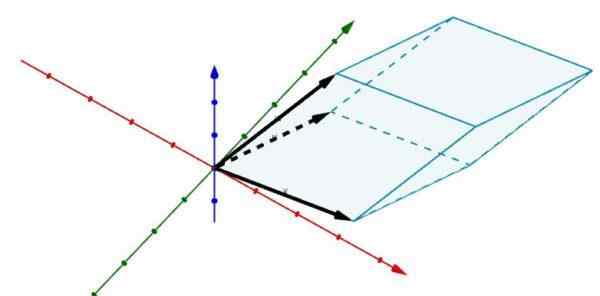
Usar determinantes nos dá isso

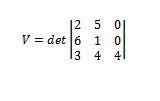
Assim, temos que o volume do referido paralelepípede é 112.

Ambos são maneiras equivalentes de calcular o volume.

Paralelepípedo perfeito

É conhecido como Euler Brick (ou Bloco Euler) em um ortoedro que cumpre a propriedade de que tanto o comprimento de suas bordas quanto o comprimento das diagonais de cada um de seus rostos são números inteiros.

Enquanto Euler não foi o primeiro cientista a estudar os ortoedores que conhecem essa propriedade, ele encontrou resultados interessantes sobre eles.

O menor tijolo Euler foi descoberto por Paul Halcke (1662-1731) e os comprimentos de suas bordas são A = 44, B = 117 e C = 240.

Um problema aberto na teoria dos números é o seguinte:

Existem ortoedores perfeitos?

Atualmente, essa pergunta ainda não tem resposta, pois não foi possível provar que não há corpos, mas ninguém foi encontrado.

O que foi demonstrado até agora é que o paralelepípedo perfeito faz. O primeiro a ser descoberto tem como comprimento de suas bordas os valores 103, 106 e 271.

Referências

1. Cara, r. (1981). Problemas não resolvidos na teoria dos números. Springer.
2. Landaverde, f. d. (1997). Geometria. Progresso.
3. Leithold, l. (1992). O cálculo com geometria analítica. Harla, s.PARA.
4. Rendon, a. (2004). Desenho técnico: Notebook de Atividade 3 2º Bacharelado. Tebar.
5. Resnick, r., Halliday, d., & Krane, K. (2001). Vol Physics. 1. México: Continental.