Papomudas

Qual é os Papomudas?

Ele Papomudas É um procedimento para resolver expressões algébricas. Seu acrônimo indica a ordem de prioridade das operações: parênteses, poderes, multiplicação, divisão, adição e subtração. Usando esta palavra, você pode lembrar facilmente a ordem em que uma expressão composta por várias operações deve ser resolvida.

Geralmente, em expressões numéricas, você pode encontrar várias operações aritméticas juntas, como somas, subtração, multiplicações e divisões, que também podem ser frações, poderes e raízes. Para resolvê -los, é necessário seguir um procedimento que garante que os resultados estejam corretos.

Uma expressão aritmética que consiste em uma combinação dessas operações deve ser resolvida de acordo com a prioridade da ordem, também conhecida como hierarquia de operações, estabelecida há muito tempo em convenções universais. Assim, todas as pessoas podem seguir o mesmo procedimento e obter o mesmo resultado.

Caracteristicas

O Papomudas é um procedimento padrão que estabelece a ordem que deve ser seguida quando uma expressão deve ser dada, que é composta por uma combinação de operações como soma da subtração, multiplicação e divisão.

Este procedimento estabelece a ordem de prioridade de uma operação em relação aos outros no momento em que serão; ou seja, cada operação tem uma mudança ou nível hierárquico a ser resolvido.

A ordem em que as diferentes operações de uma expressão devem ser resolvidas é dada por cada sigla da palavra papomudas. Dessa forma, você tem que:

1. PA: parênteses, suportes quadrados ou chaves.
2. PO: poderes e raízes.
3. MU: multiplicações.
4. D: Divisões.
5. A: Adições ou somas.
6. S: subtrações ou subtração.

Este procedimento também é chamado em inglês como PEMDAS; Lembrar facilmente que esta palavra está associada à frase: "Por favor, desculpe minha querida tia Sally”, Onde cada letra inicial corresponde a uma operação aritmética, da mesma maneira que as Papomudas.

Como resolvê -los?

Com base na hierarquia estabelecida por Papomudas para resolver as operações de uma expressão, é necessário cumprir a seguinte ordem:

• Primeiro, todas as operações que estão dentro dos símbolos de agrupamento, como parênteses, chaves, suportes e barras de fração devem ser resolvidas. Quando há símbolos de agrupamento dentro de outros, você deve começar a calcular de dentro.

Pode servir a você: sucessões quadráticas: exemplos, regra e exercícios resolvidos

Esses símbolos são usados ​​para alterar a ordem em que as operações são resolvidas, porque o que está sempre dentro deles deve sempre ser resolvido.

• Então os poderes e raízes são resolvidos.
• Em terceiro lugar, multiplicações e divisões são resolvidas. Estes têm a mesma ordem de prioridade; Portanto, quando essas duas operações são encontradas em uma expressão, a que aparece primeiro deve ser resolvida, lendo a expressão da esquerda para a direita.
• Em última análise.
• As operações nunca devem ser misturadas quando lidas da esquerda para a direita, você sempre deve seguir a ordem de prioridade ou hierarquia estabelecida pelos Papomudas.

É importante lembrar que o resultado de cada operação deve ser colocado na mesma ordem em relação aos outros, e todas as etapas intermediárias devem ser separadas por um sinal até atingir o resultado final.

Aplicativo

O procedimento de Papomudas é usado quando você tem uma combinação de operações diferentes. Levando em consideração como eles são resolvidos, isso pode ser aplicado em:

Expressões contendo somas e subtrações

É uma das operações mais simples, porque ambas têm a mesma ordem de prioridade, de modo que ela deve ser resolvida a partir da esquerda para a direita na expressão; por exemplo:

22 -15 + 8 +6 = 21.

Expressões contendo somas, subtração e multiplicações

Nesse caso, a operação de maior prioridade é a multiplicação, então as somas e a subtração são resolvidas (a que é a primeira na expressão). Por exemplo:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Expressões contendo soma, multiplicação e divisão de subtração

Nesse caso, há uma combinação de todas as operações. Começa resolvendo a multiplicação e a divisão que têm prioridade superior, depois as somas e a subtração. Lendo a expressão da esquerda para a direita, ela é resolvida de acordo com sua hierarquia e posição dentro da expressão; por exemplo:

Pode servir você: Mumm

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Expressões contendo soma, subtração, multiplicação, divisão e poderes

Nesse caso, um dos números é elevado a um poder, que dentro do nível de prioridade deve ser resolvido primeiro e depois resolver multiplicações e divisões e, finalmente, as somas e a subtração:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

Como os poderes, as raízes também têm a segunda ordem de prioridade; Portanto, em expressões que os contêm, eles devem primeiro ser resolvidos do que multiplicações, divisões, somas e subtração:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Expressões que usam símbolos de agrupamento

Quando sinais são usados, como parênteses, chaves, suportes e barras de frações, que estão dentro delas são resolvidas primeiro, independentemente da ordem de prioridade das operações que ela contém em relação àqueles fora disso, como se lidar com um separado expressão:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Se existem várias operações, elas devem ser resolvidas por ordem hierárquica. Em seguida, as outras operações que compõem a expressão são resolvidas; por exemplo:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

Em algumas expressões, são usados ​​símbolos de agrupamento dentro de outros, como quando é necessário mudar o sinal de uma operação. Nesses casos, deve começar resolvendo de dentro para fora; isto é, simplificando os símbolos de agrupamento que estão no centro de uma expressão.

Geralmente, a ordem para resolver operações contidas nesses símbolos é: primeiro resolva o que está entre parênteses (), depois colchetes [] e finalmente as chaves .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Pode servir a você: probabilidade teórica: como divulgá -lo, exemplos, exercícios

= 90 - 3 _* 24

= 90 - 72

= 18.

Exercícios

Primeiro exercício

Encontre o valor da seguinte expressão:

vinte² + √225 - 155 + 130.

Solução

Aplicando os papomudas, os poderes e as raízes devem ser resolvidos primeiro e depois adiciona e subtração. Nesse caso, as duas primeiras operações pertencem à mesma ordem, então a que é primeiro é resolvida, a partir da esquerda para a direita:

vinte² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Em seguida, adicione e subtração, começando à esquerda também:

400 + 15 -155 + 130

= 390.

Segundo exercício

Encontre o valor da seguinte expressão:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Solução

Começa resolvendo as operações que estão dentro dos parênteses, seguindo a ordem hierárquica que eles possuem de acordo com os Papomudas.

Primeiro, os poderes dos primeiros parênteses são resolvidos, então as operações do segundo parêntese são resolvidas. Como eles pertencem à mesma ordem, a primeira operação da expressão é resolvida:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216- 729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Como as operações nos parênteses já foram resolvidas, agora a divisão que tem a maior hierarquia continua:

[- (-513) ÷ (3)] = [- (-171)]].

Finalmente, os parênteses que separam o sinal menos (-) do resultado, que neste caso é negativo, indica que uma multiplicação desses sinais deve ser feita. Assim, o resultado da expressão é:

[- (-171)] = 171.

Terceiro exercício

Encontre o valor da seguinte expressão:

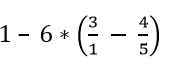
Solução

As frações que estão dentro dos parênteses são resolvidas:

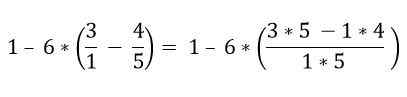
Dentro dos parênteses, existem várias operações. As multiplicações são resolvidas pela primeira vez e depois as subtrações; Nesse caso, a barra de fração é considerada como um símbolo de agrupamento e não como uma divisão; portanto, as operações da parte superior e inferior devem ser resolvidas:

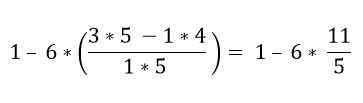
Por ordem hierárquica, a multiplicação deve ser resolvida:

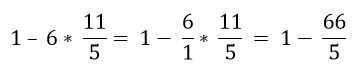
Finalmente, a subtração é resolvida: