Orthoedro fórmulas, área, volume, diagonal, exemplos

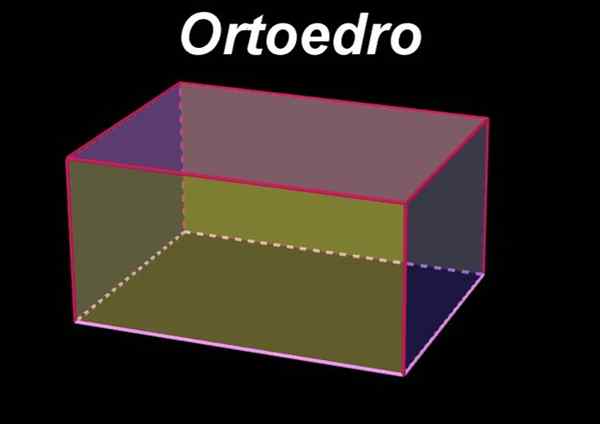
Ele Orthoedro É uma figura geométrica volumétrica ou tridimensional que é caracterizada por ter seis faces retangulares, de modo que faces opostas estão em planos paralelos e são retângulos idênticos ou congruentes entre si. Por outro lado, os rostos adjacentes a um determinado rosto estão em aviões perpendiculares à do rosto inicial.

Também pode ser considerado quando Orthoedro como um prisma da base retangular ortogonal, em que ângulos de dihedros Formados pelos planos de dois lidados adjacentes a uma borda comum, eles medem 90º. O ângulo diédrico entre duas faces é medido na interseção de faces com um plano perpendicular e comum para eles.

figura 1. Orthoedro. Fonte: f. Zapata com geogebra.

Da mesma forma, o Orthoedro é um retângulo paralelepiped, já que isso é definido para o paralelepípedo como a figura volumétrica de seis faces, que são paralelas dois a dois.

Em qualquer paralelepípedia, as faces são paralelogramas, mas no retângulo paralelepipe as faces devem ser retangulares.

[TOC]

Partes do Orthoedro

As partes de um poliedro, como o Orthoedro, são:

-Arestas

-Vértices 

-Rostos

O ângulo entre duas bordas de uma face do ortoedro coincide com o ângulo diédrico formado por suas outras duas faces adjacentes a cada uma das bordas, formando ângulo reto. A imagem a seguir esclarece cada conceito:

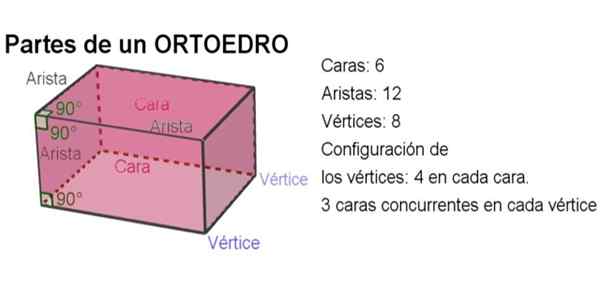Figura 2. Partes de um ortoedro. Fonte: f. Zapata com geogebra.

-No total, um ortoedro tem 6 faces, 12 arestas e 8 vértices.

-O ângulo entre duas bordas é um ângulo reto.

-O ângulo diédrico entre dois lados também é reto.

-Em cada rosto, existem quatro vértices e em cada vértice três rostos mutuamente ortogonais participam.

Pode atendê -lo: o que é um número Capicúa? Propriedades e exemplos

Fórmulas Orthoedro

Área

A superfície ou área de um Orthoedro É a soma das áreas de seus rostos.

Se as três arestas que concordam em um vértice têm medidas A, B e C, como mostrado na Figura 3, a face frontal tem uma área C⋅b E a face de fundo também possui uma área C⋅b.

Então, os dois rostos laterais têm uma área A⋅b cada uma. E, finalmente, os rostos do piso e o telhado têm área A⋅c cada uma.

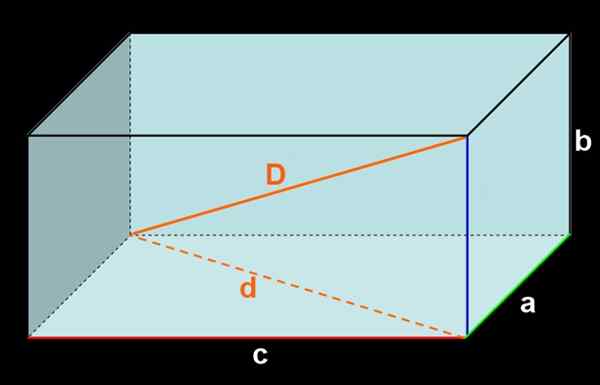Figura 3. Ortoedro de dimensões a, b, c. Diagonal interno D e diagonal externa D.

Adicionando a área de todas as faces é obtida:

A = 2⋅c⋅b + 2⋅A⋅B + 2⋅A

Desenhando fator comum e ordenando os termos:

A = 2⋅ (a⋅b + b⋅c + c⋅a)

Volume

Se o Orthoedro é considerado um prisma, seu volume será calculado da seguinte forma:

Volume = área base do prisma x a altura do prisma

Nesse caso, o piso das dimensões é considerado um retangular c e para, Então a área base é C⋅A.

A altura é dada pelo comprimento b Das bordas ortogonais para as laterais para e c.

Multiplicando a área base (A⋅c) por altura b Você tem o volume V Do Orthoedro:

V = a⋅b⋅c

Diagonal interna

Em um ortoedro, existem dois tipos de diagonais: diagonais externas e diagonais internas.

As diagonais externas estão em faces retangulares, enquanto as diagonais internas são os segmentos que se juntam a dois vértices opostos, sendo entendidos por vértices opostos que não compartilham nenhuma vantagem.

Em um ortoedro, existem quatro diagonais internos, toda a mesma medida. A duração das diagonais internas pode ser obtida na aplicação do teorema de Pitágoras para retângulos.

Pode atendê -lo: funções trigonométricas: básico, no avião cartesiano, exemplos, exercícios

O comprimento d da diagonal externa do piso ortoedro cumpre o relacionamento pitagórico:

d² = a² + c²

Da mesma forma, a diagonal de medição interior do relacionamento pitagoroso:

D² = d² + b².

Combinando as duas expressões anteriores que você tem:

D² = a² + c² + b².

Finalmente, a duração de qualquer uma das diagonais internas do Orthoedro é dada pela seguinte fórmula:

D = √ (a² + b² + c² ). 

Exemplos

- Exemplo 1

Um pedreiro constrói um tanque em forma de ortoedro cujas dimensões internas são: 6 m x 4 m de base e 2 m de altura. É solicitado:

a) determinar a superfície interna do tanque se estiver completamente aberta em sua parte superior. 

b) Calcule o volume do espaço interior do tanque.

c) Encontre o comprimento de uma diagonal interior.

d) Qual é a capacidade do tanque em litros?

Solução para

Tomaremos as dimensões da base retangular A = 4 me

A área de um ortoedro com as dimensões dada é dada pelo seguinte relacionamento:

A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)

Quer dizer:

A = 2⋅ (8 m² + 12 m² + 24 m²) = 2⋅ (44 m²) = 88 m²

O resultado anterior é a área do Orthoedro fechada com as dimensões dadas, mas como é um tanque completamente descoberto em sua parte superior, para obter a superfície das paredes internas do tanque, a área da tampa que faltava aquilo é:

C⋅A = 6 m ⋅ 4 m = 24 m².

Finalmente, a superfície interior do tanque será: s = 88 m² - 24 m² = 64 m².

Solução b

O volume interior do tanque é dado pelo volume de um ortoedro das dimensões internas do tanque:

V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m³.

Solução c

A diagonal interior de um octaedro com as dimensões do interior do tanque tem um comprimento dado por:

Pode atendê -lo: variável aleatória contínua

√ (a² + b² + c² ) = √ ((4 m)² + (2 m)² + (6 m)² )

Executando as operações indicadas que temos:

D = √ (16 m² + 4 m² + 36 m² ) = √ (56 m²) = 2√ (14) m = 7,48 m.

Solução d

Para calcular a capacidade do tanque em litros, é necessário saber que o volume de um decímetro cúbico é equivalente à capacidade de um litro. Foi calculado anteriormente em volume em metros cúbicos, mas deve ser transformado em decímetros cúbicos e depois em litros:

V = 48 m³ = 48 (10 dm)³ = 4.800 dm³ = 4.800 l

- Exercício 2

Um aquário de vidro tem uma forma cúbica de 25 cm. Determine a área em M², O volume em litros e o comprimento de uma diagonal interior em CM.

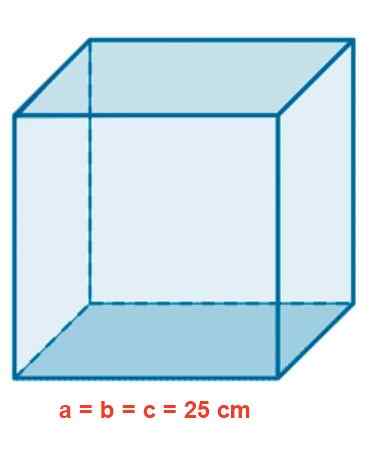Figura 4. Aquário de vidro cúbico.

Solução

A área é calculada pela mesma fórmula Orthoedro, mas levando em consideração que todas as dimensões são idênticas:

A = 2⋅ (3 a⋅a) = 6⋅ A² = 6⋅ (25 cm)² = 1.250 cm²

O volume do cubo é dado por:

V = a³ = (25 cm)³ = 15.625 cm³ = 15.625 (0,1 dm)³ = 15.625 dm³ = 15.625 l.

O comprimento d da diagonal interior é:

D = √ (3ª²) = 25√ (3) cm = 43,30 cm.

Referências

1. Arias j. Geogebra: Prism. Recuperado de: youtube.com.
2. Cálculo.DC. Exercícios e problemas resolvidos em áreas e volumes. Recuperado de: cálculo.DC.
3. Salvador r. Pirâmide + orthoedro com geogebra (IHM). Recuperado de: youtube.com
4. Weisstein, Eric. "Ortoedro". Mathworld. Pesquisa de Wolfram.
5. Wikipedia. Orthoedro. Recuperado de: é.Wikipedia.com