Notação desenvolvida o que é, exemplos e exercícios
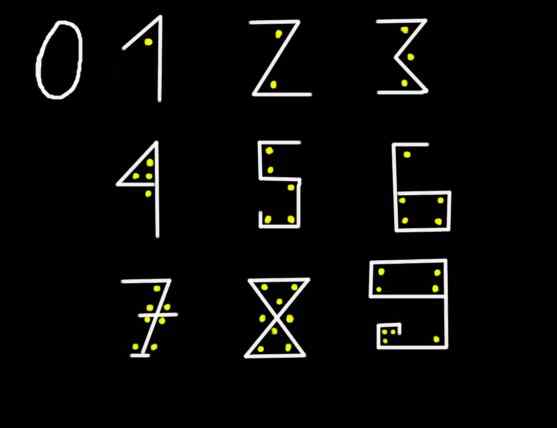
- 1485
- 274
- Orlando MacGyver
O notação desenvolvida É aquele em que uma figura numérica é expressa como uma soma na qual o valor posicional de cada dígito que forma o número é levado em consideração.
Por exemplo, ao escrever uma figura como 2345 cada dígito tem uma hierarquia posicional. Leitura do dígito extremo direito à esquerda, a hierarquia ou valor está crescendo.
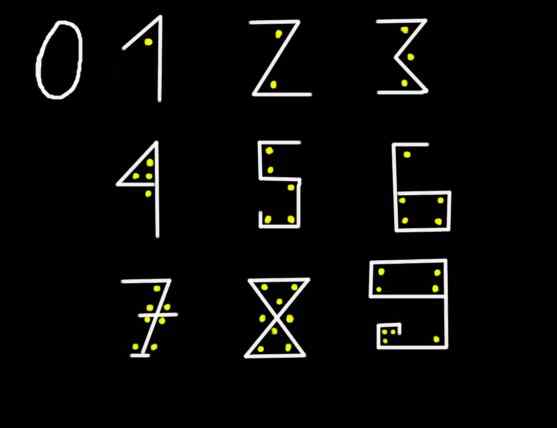 figura 1. Com nove grafemas, é possível representar qualquer figura.
figura 1. Com nove grafemas, é possível representar qualquer figura. Na Figura 2345, o dígito 5 representa cinco unidades, o dígito 4 representa quatro dezenas, o 3 corresponde à terceira posição da esquerda para a direita e, portanto, os 3 representam três centenas, finalmente os 2 representam dois mil. Ou seja, em notação desenvolvida ou estendida, a Figura 2345 é escrita assim:
2345 = 2 milhares + 3 cem + 4 dezenas + 5 unidades
Mas também pode ser expresso da seguinte maneira:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
A Figura 2345 também pode ser escrita como a soma dos poderes de 10:
2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0
Onde o circunferência significa aumentar o expoente indicado. Por exemplo, 10^3 = 10 x 10 x 10 = 1000. Outra maneira de escrever os expoentes é através de uma supervisão:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100
[TOC]
Sistema de numeração posicional
O sistema de números árabes são os números usados diariamente na grande maioria dos continentes e países do mundo. Os números árabes são um sistema base 10 porque dez símbolos ou grafemas são usados para escrever qualquer número. Esses dez símbolos são:
0 1 2 3 4 5 6 7 8 9
Com apenas um desses símbolos, as figuras entre zero e nove podem ser expressas. Para expressar números maiores que nove, o sistema posicional baseado em dez. A Figura 10 é uma dúzia e zero unidades. A Figura 11 é uma dúzia e uma unidade. A Figura 123 (cento e vinte e três) é cento, duas dezenas e três unidades. Escrito na forma de poderes de dez, o número 123 será:
Pode atendê -lo: 60 divisores1 × 10^2 + 2 × 10^1 + 3 × 10^0
Onde:
10^2 = 10 x 10 = 100
10^1 = 10
10^0 = 1.
Com este exemplo, fica claro que a posição do dígito no final é a posição 0 e representa o número de unidades, o do segundo dígito da direita para a esquerda é a posição 1 e representa o número de dezenas, o terceiro dígito (direita para a esquerda) tem a posição 2 e representa as centenas.
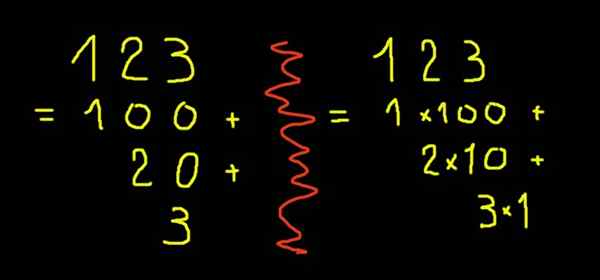 Figura 2. Notação desenvolvida da Figura 123.
Figura 2. Notação desenvolvida da Figura 123. Números fracionários ou decimais
Com o sistema posicional decimal, também é possível.
Para representar a fração ½ no sistema decimal árabe, ou seja, metade da unidade é escrita:
½ = 0,5
Para alcançar essa expressão em nosso sistema com base em 10, as seguintes operações foram feitas:
1- Multiplique numerador e denominador para 5 para ter a fração equivalente 5/10 = 1/2.
2- A divisão por 10 é equivalente a multiplicar pelo poder com base em dez com expoente menos um (10^-1), ou seja, 5/10 = 5 × 10^-1.
3- O expoente negativo indica quantas vezes o dígito indicado na posição da unidade é executado ou posicionado; no nosso caso, seria 0,5.
4- ½ = 0,5 em notação estendida de que está escrita assim:
0,5 = 0x10^0 + 5 × 10^-1
Onde 10^-1 = 0,1 é uma décima (a fração correspondente à unidade dividida em 10 partes iguais).
Dessa forma, o número 0,5 corresponde a cinco décimos, mas o número 0,05 corresponde a 5 centésimos e 0,005 a 5 milésimos.
Pode atendê -lo: por que a álgebra é importante em certas situações da vida cotidiana?Exemplos de notação desenvolvidos
Exemplo 1
Dado o número 40201 na notação padrão, converta -a na notação desenvolvida.
Solução:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Exemplo 2
Escreva a fração ¾ em notação estendida.
Solução:
Nesse caso, existem três quartos da unidade.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10^-1 + 5 × 10^-2.
Disse em palavras que seria assim:
A fração ¾ corresponde a sete décimos mais quinhentos centésimos.
Exercícios de notação desenvolvidos
Exercício 1
Diga em palavras a expressão desenvolvida da figura 40201 do Exemplo 1.
Solução:
A notação desenvolvida é assim:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Que na linguagem da palavra é dito:
Quatro dezenas de milhares, mais milhares, além de duzentos, mais zero dezenas, além de uma unidade.
Exercício 2
Expressar nas palavras a figura anterior e quebrar a frase correspondente desenvolvida.
Solução:
O número 40201 em palavras é expresso da seguinte maneira:
Quarenta mil duzentos e dois
A frase anterior pode se desenvolver como:
40 × 1000 + 2 × 100 + 1
Pode -se dizer que a maneira de pronunciar as figuras é uma maneira meio desenvolvida de expressá -lo.
Exercício 3
Escreva a maneira desenvolvida número 7/3.
Solução:
É uma figura expressa como uma fração inadequada, pois como o numerador é maior que o denominador, a figura é maior que a unidade.
Esta fração inadequada pode ser quebrada como a soma das frações 6/3 + 1/3. A primeira das frações resulta em um número inteiro 2, enquanto 1/3 = 0,333333, onde o dígito 3 é repetido indefinidamente. Para que a expressão decimal desenvolvida da figura 7/3 seja sempre uma expressão aproximada:
Pode servir a você: quadrilateral: elementos, propriedades, classificação, exemplos7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.
Exercício 6
Escreva em notação padrão e depois desenvolveu o número: Vinte -três bilhões de duzentos e cinquenta milhões quinhentos e vinte e mil mil e trezentos vinte e cinco com três vinte e três milésimos.
Solução:
Deve -se lembrar que um Millardo é o equivalente a um bilhão. Palavra Millardo Foi aceito pela Academia Real Espanhola em 1995, a pedido do falecido presidente venezuelano Rafael Caldera, membro da Academia de Linguagem Venezuelana. Nesse caso, a figura da notação padrão é escrita da seguinte maneira:
23.2501526.325.023
23 bilhões + 250 milhões + 526 mil + 325 unidades + 23 milésimos.
23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3
Finalmente, a figura na notação desenvolvida está escrita:
2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.
Referências
- Academia Khan. Tabelas de valor posicional. Recuperado de: é.Khanacademy.org
- Academia Khan. Escreva um número desenvolvido (vídeo). Recuperado de: é.Khanacademy.org
- Ifrah, Geoges (1998): História Universal das Figuras. Espasa Calpe s.PARA.
- Wikipedia. Notação posicional. Recuperado de: é.Wikipedia.com
- Wikipedia. Millardo. Recuperado de: é.Wikipedia.com
- « Estrutura de óxido de fósforo (v), propriedades, obtenção, uso, riscos
- Estrutura de fosfato de alumínio (alpo4), propriedades, obtenção, uso »

