Números primos característicos, exemplos, exercícios

O números primos, Também chamados de primos absolutos, são aqueles números naturais que são divisíveis apenas entre si e 1. Nesta categoria, números como: 2, 3, 5, 7, 11, 13, 17, 19, 23 e muitos mais vêm nesta categoria.

Por outro lado, um número composto é divisível por si só, por 1 e pelo menos mais um número. Temos, por exemplo, em 12, que é divisível por 1, 2, 4, 6 e 12. Por convenção, o 1 não está incluído na lista de números primos ou nos compostos.

figura 1. Alguns números primos. Fonte: Wikimedia Commons.

O conhecimento dos números primos data dos tempos remotos; Os antigos egípcios já os manipularam e certamente eram conhecidos muito antes.

Esses números são muito importantes, pois qualquer número natural pode ser representado pelo produto de números primos, sendo essa representação única, exceto na ordem dos fatores.

Este fato está totalmente estabelecido em um teorema chamado O teorema fundamental da aritmética, que afirma que os números que não são primos são necessariamente compostos por produtos de números que são.

[TOC]

Características dos números primos

Abaixo das principais características dos números primos:

-Eles são infinitos, pois, por mais grande um número primo, sempre pode ser encontrado.

-Se um número primo p não se divide exatamente em outro número para, É então dito que p e para Eles são primos uns com os outros. Quando isso acontece, o único divisor comum ambos é 1.

Não é necessário para Seja primo absoluto. Por exemplo, os 5 são primo e, embora os 12 não sejam, ambos os números são primos entre si, já que os dois têm um divisor comum para 1.

-Quando um número primo p Divida um poder do número n, Também divide um n. Considere 100, que é um poder de 10, especificamente 10². Acontece que os 2 dividem 100 e 10.

-Todos os números primos são ímpares, exceto 2, portanto, seu último dígito é 1, 3, 7 ou 9. O 5 não está incluído, porque, embora seja estranho e primo, nunca é a figura final de outro número primo. De fato, todos os números que terminam em 5 são múltiplos disso e, portanto, não são primos.

Pode atendê -lo: simetria central: propriedades, exemplos e exercícios

-Sim p É primo e divisor do produto de dois números para.b, então p Divida um deles. Por exemplo, o principal número 3 divide o produto 9 x 11 = 99, já que 3 é um divisor de 9.

Como saber se um número é primo

O Primalidade É o nome dado à qualidade de ser primo. Bem, matemática francesa Pequeno teorema de Fermat, Isso diz isso:

"Dado um número natural de primo p e qualquer número natural para maior que 0, é cumprido que para^p - para É um múltiplo de p, sempre e quando p ser primo ".

Podemos corroborar isso usando números pequenos, por exemplo, suponha P = 4, que já sabemos que não é primo e a = 6:

6⁴ - 6 = 1296 - 6 = 1290

O número 1290 não é exatamente divisível entre 4, portanto 4 não é um número primo.

Vamos fazer o teste agora com p = 5, que é primo e a = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 é divisível entre 5, pois qualquer número que termina em 0 ou 5 é. De fato 7760/5 = 1554. Como o pequeno teorema de Fermat é cumprido, podemos garantir que 5 seja um número primo.

O teste através do teorema é eficaz e direto com pequenos números, nos quais a operação é fácil de executar, mas o que fazer se eles nos pedir para descobrir a primalidade de um grande número?

Nesse caso, o número é dividido sucessivamente entre todos os números primos menores, até que alguma divisão exata ou que o quociente seja menor que o divisor.

Se alguma divisão for exata, significa que o número é composto e se o quociente for menor que o divisor, significa que o número é primo. Vamos colocá -lo em prática no ano resolvido 2.

Maneiras de encontrar um número primo

Existem números primos infinitos e não há fórmula única para determinar. No entanto, observar alguns números primos como esses:

Pode servir a você: ângulo nulo: definição e características, exemplos, exercícios

3, 7, 31, 127 ..

Observa -se que eles estão na forma 2ⁿ - 1, com n = 2, 3, 5, 7, 9 ... Garantimos:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Mas não podemos garantir que em geral 2ⁿ - 1 ser primo, porque existem alguns valores de n para o qual não funciona, por exemplo, em 4:

2⁴ - 1 = 16 - 1 = 15

E o número 15 não é primo, pois termina em 5. No entanto, um dos maiores números primos conhecidos, encontrados por cálculos feitos por computador, está na forma 2ⁿ - 1 com:

N = 57.885.161

O Fórmula de Mersenne Garanta -nos que 2^p - 1 é sempre primo, desde que p Seja primo também. Por exemplo, o 31 é primo, então é certo que 2³¹ - 1 também é:

2³¹ - 1 = 2.147.483.647

No entanto, a fórmula permite que apenas alguns números primos sejam determinados, não todos.

Fórmula de Euler

O polinômio a seguir permite encontrar números primos, desde que n esteja entre 0 e 39:

P (n) = n² + N + 41

Mais tarde, na seção de exercícios resolvidos, há um exemplo de seu uso.

A triagem Eratostenes

Eratóstenes era um físico e matemático da Grécia antiga que viveu no terceiro século para.C. Ele desenvolveu um método gráfico de encontrar os números primos que podemos colocar em prática com pequenos números, é chamado de tela Eratóstenes (uma tela é como um filtro).

-Os números são colocados em uma mesa como a mostrada na animação.

-Então os números pares são rotulados, exceto os 2 que sabemos que é primo. Todos os outros são múltiplos disso e, portanto, não são primos.

-Os múltiplos de 3, 5, 7 e 11 também são marcados, excluindo todos porque sabemos que eles são primos.

-Os múltiplos de 4, 6, 8, 9 e 10 já estão marcados, porque são compostos e, portanto, múltiplos de qualquer um dos primos indicados.

Pode atendê -lo: História da trigonometria de suas origens

-Finalmente, os números restantes não estão marcados são primos.

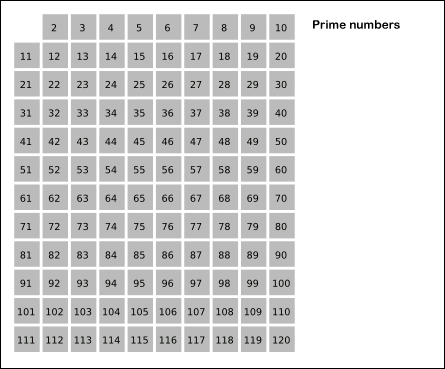Figura 2. Animação de triagem de Eratostenes. Fonte: Wikimedia Commons.

Exercícios

- Exercício 1

Usando o polinômio Euler para números primos, encontre 3 números maiores que 100.

Solução

Este é o polinômio que Euler propôs encontrar números primos, que opera para n valores entre 0 e 39.

P (n) = n² + N + 41

Através da Tanteo, selecionamos um valor de n, por exemplo, n = 8:

P (8) = 8² + 8 + 41 = 113

Como n = 8 produz um número primo maior que 100, avaliamos o polinômio para n = 9 e n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Exercício 2

Descubra se os seguintes números são primos:

a) 13

b) 191

Solução para

O 13 é pequeno o suficiente para usar o pequeno teorema de Fermat e a ajuda da calculadora.

Usamos A = 2 para que os números não sejam muito grandes, embora também possam ser usados ​​a = 3, 4 ou 5:

2¹³ - 2 = 8190

8190 é divisível entre 2, pois é par, portanto 13 é primo. O leitor pode corroborá -lo fazendo o mesmo teste com a = 3.

Solução b

191 é muito grande para experimentar o teorema e uma calculadora comum, mas podemos levar a divisão entre cada número primo. Omitimos dividir por 2 porque 191 não é par e a divisão não será exata ou a proporção menor que 2.

Tentamos dividir por 3:

191/3 = 63.666…

E não dá exato, nem o quociente é menor que o divisor (63.666 ... é maior que 3)

Continuamos testando 191 pelos primos 5, 7, 11, 13 e a divisão exata não é alcançada, nem a proporção menor que o divisor. Até que se divida entre 17:

191/17 = 11, 2352 ..

Como não é exato e 11.2352 ... é menor que 17, o número 191 é primo.

Referências

1. Baldor, a. 1986. Aritmética. Edições e distribuições Codex.
2. Prieto, c. Números primos. Recuperado de: páginas.Matem.Unam.mx.
3. Propriedades de números primos. Recuperado de: mae.Ufl.Edu.
4. Smartick. Números Primo: Como encontrá -los com a peneira de Eratostenes. Recuperado de: Smartick.é.
5. Wikipedia. Número primo. Recuperado de: é.Wikipedia.org.