Propriedades de números complexos, exemplos, operações

O números complexos Eles são o conjunto numérico que cobre os números reais e todas as raízes dos polinômios, incluindo as raízes uniformes dos números negativos. Essas raízes não existem no conjunto de números reais, mas em números complexos é a solução.

Um número complexo consiste em uma parte real e outra chamada "imaginária". A parte real é chamada para, Por exemplo, e a parte imaginária Ib, com para e b números reais e "eu" gosto do Unidade imaginária. Dessa maneira, o número complexo assume o formulário:

Z = a + ib

figura 1.- Representação binomial de um número complexo em termos de parte real e parte imaginária. Fonte: Pixabay.

Exemplos de números complexos são 2 - 3i, -πi, 1 + (1/2) I. Mas antes de operar com eles, vamos ver de onde a unidade imaginária se origina Yo, Considerando esta equação quadrática:

x² - 10x + 34 = 0

Em que a = 1, b = -10 e c = 34.

Quando a fórmula do solvente é aplicada para determinar a solução, encontramos o seguinte:

Como determinar o valor de √-36? Não há número real de que o quadrado seja uma quantidade negativa. Então conclui -se que esta equação não tem soluções reais.

No entanto, podemos escrever isso:

√-36 = √-6² = √6² (-1) = 6√-1

Se definirmos um certo valor x tal que:

x² = -1

Então:

x = ± √-1

E a equação anterior teria uma solução. Portanto, a unidade imaginária foi definida como:

I = √-1

E assim:

√-36 = 6i

Muitos matemáticos da antiguidade trabalharam na solução de problemas semelhantes, destacando o Renaissance Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) e Raffaele Bombelli (1526-1572).

Anos depois, René Descartes (1596-1650) chamou "imaginário" para quantidades como o √-36 do exemplo. Por esse motivo, o √-1 é conhecido como o Unidade imaginária.

[TOC]

Propriedades de números complexos

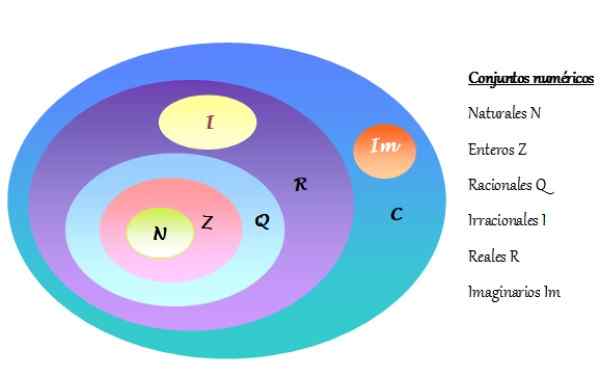
-O conjunto de números complexos é indicado como C e inclui números reais r e números imaginários im. Os conjuntos numéricos são representados em um diagrama de Venn, como mostrado na figura a seguir:

Pode atendê -lo: exercícios de fatoração resolvidos Figura 2. Diagrama de Venn de conjuntos numéricos. Fonte: f. Zapata.

-Todo número complexo consiste em uma parte real e outra parte imaginária.

-Quando a parte imaginária de um número complexo é 0, é um número real puro.

-Se a parte real de um número complexo for 0, o número é puro imaginário.

-Dois números complexos são os mesmos se sua respectiva parte real e parte imaginária forem iguais.

-Com os números complexos, são realizadas as operações conhecidas de somas, subtração, multiplicação, produto e empoderamento, resultando em outro número complexo.

Representação de números complexos

Números complexos podem ser representados de várias maneiras. Aqui estão os principais:

- Forma binômica

É a forma dada no começo, onde z é o número complexo, para é a parte real, b é a parte imaginária e Yo É a unidade imaginária:

Z = a + ib

Ou também:

Z = x + iy

Uma maneira de representar graficamente o número complexo é através do plano complexo mostrado nesta figura. O eixo imaginário é vertical, enquanto o eixo real é horizontal e denota como re.

O número complexo z Está representado neste avião como um ponto de coordenada (X, y) qualquer (A, b), Como é feito com os pontos do avião real.

A distância da origem ao ponto Z é o módulo do número complexo, indicado como r, enquanto φ é o ângulo que se forma r Com o eixo real.

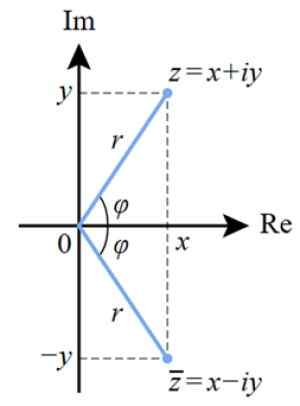Figura 3. Representação de um número complexo no plano complexo. Fonte: Wikimedia Commons.

Esta representação está intimamente relacionada à dos vetores no plano real. O valor de r corresponde a módulo do número complexo.

Pode atendê-lo: Método Gauss-Seidel: Explicação, Aplicações, Exemplos

- Forma polar

A forma polar consiste em expressar o número complexo, dando os valores de r e de φ. Se olharmos para a figura, o valor de r Corresponde à hipotenusa de um triângulo certo. As categorias valem para e b, o bem x e e.

Na forma binomial ou binomial, podemos passar para a forma polar por:

R = √x²+e²

O ângulo φ É o que forma o segmento R com o eixo horizontal ou eixo imaginário. É conhecido como argumento do número complexo. Desta maneira:

φ = arctg (y/x)

O argumento tem valores infinitos, levando em consideração que toda vez que um retorno é girado, que vale 2π radianes, r novamente ocupa a mesma posição. Dessa maneira em geral, o argumento de Z, denotado arg (z), é expresso da seguinte forma:

Arg (z) = φ + 2kπ

Onde k é inteiro e serve para indicar a quantidade de voltas giradas: 2, 3, 4 .. . O sinal indica o significado da rotação, se o tempo ou o anti -marário for feito.

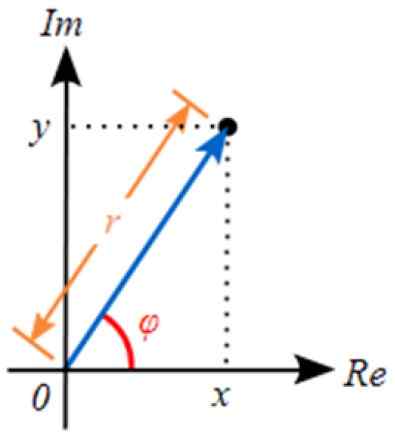Figura 4. Representação polar de um número complexo no plano complexo. Fonte: Wikimedia Commons.

E se queremos passar na forma polar para a forma binomial, usamos motivos trigonométricos. A partir da figura anterior, podemos ver que:

x = r cos φ

y = r sen φ

Dessa maneira, z = r (cos φ+i sin φ)

Que é abreviado assim:

z = r cis φ

Exemplos de números complexos

Os seguintes números complexos são dados binomialmente:

a) 3 + eu

b) 4

d) -6i

E estes em um torque ordenado:

a) (-5, -3)

b) (0, 9)

c) (7.0)

Finalmente, este grupo recebe polar ou trigonométrico:

a) √2 cis 45º

b) √3 cis 30º

Pode servir a você: distribuição hipergeométrica: fórmulas, equações, modelo

c) 2 cis 315º

Para que servem?

A utilidade dos números complexos vai além da resolução da equação de segundo grau mostrada no início, pois são essenciais no campo da engenharia e da física, especialmente em:

-O estudo de ondas eletromagnéticas

-Análise alternativa de corrente e tensão

-A modelagem de todos os tipos de sinais

-Teoria da relatividade, onde o tempo é assumido como uma magnitude imaginária.

Operações com números complexos

Com os números complexos, podemos executar todas as operações que são feitas com o real. Alguns são mais fáceis de fazer se os números vieram binomicamente, como soma e subtração. Por outro lado, multiplicação e divisão são mais simples se forem realizadas com a forma polar.

Vejamos alguns exemplos:

- Exemplo 1

Adicione z₁ = 2 + 5i e z₂ = -3 -8i

Solução

As peças reais são adicionadas separadamente das peças imaginárias:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Exemplo 2

Multiplique z₁ = 4 cis 45º e z₂ = 5 cis 120º

Solução

Pode -se demonstrar que o produto de dois números complexos em polar ou trigonométrico é dado por:

z₁ . z₂ = r₁.r₂ Cis (φ₁ + φ₂)

De acordo com isso:

z₁ . z₂ = (4 × 5) cis (45 + 120) = 20 cis 165º

Aplicativo

Uma aplicação simples de números complexos é encontrar todas as raízes de uma equação polinomial, como a mostrada no início do artigo.

No caso da Equação X² - 10x + 34 = 0, ao aplicar a fórmula do solvente, é obtido:

Portanto, as soluções são:

x₁ = 5 + 3i

x₂ = 5 - 3i

Referências

1. Earl, r. Números complexos. Recuperado de: matemática.boi.AC.Reino Unido.
2. Figuera, j. 2000. Matemática 1ª. Diversificado. Edições Co-Bo.
3. Hoffmann, J. 2005. Seleção de questões de matemática. Monfort Publications.
4. Jiménez, r. 2008. Álgebra. Prentice Hall.
5. Wikipedia. Números complexos. Recuperado de: em.Wikipedia.org