Ângulos e triângulos

Os ângulos e triângulos fazem parte da geometria plana. Shuttersock

O que são ângulos e triângulos?

A ângulo É a região do avião delimitada por duas semi -rigorosas com um ponto de origem em comum. Este ponto é conhecido como o vértice, Enquanto o semi -forte é chamado lados. Por outro lado, um triângulo É uma figura de três ângulos e três lados, com três vértices.

Vamos falar sobre os ângulos primeiro.

Ângulos

Existem várias maneiras de denotar os ângulos: através de letras gregas como α, β, γ, ao qual um sotaque circunflexo pode ser adicionado; com letras maiúsculas estofadas ou minúsculas, A, B, C, A, B, C; números, como 1, 2, 3 ... ou usando o símbolo do ângulo porte.

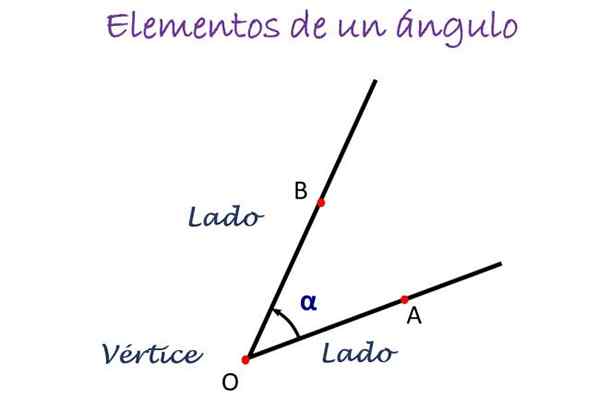Os principais elementos de um ângulo. Fonte: f. Zapata

Na figura acima, o ângulo é medido do lado A a B, indicado pela direção da seta, e no centro a letra que denota o vértice é colocado, que é normalmente ou. O ângulo é então indicado como ero AOB.

Quando o ângulo é medido em um sentido anti -horium, um sinal de A +é arbitrariamente atribuído e, se for medido em um cronograma, um sinal -para distingui -los.

A medida dos ângulos é realizada por meio de um transportador, que consiste em uma folha de plástico semicircular, como a mostrada abaixo. O semicírculo é dividido em 180 partes iguais, cada chamada grau.

Para medir, o vértice do ângulo é coincidido com o ponto central do transportador, indicado com a flecha, e o lado inicial com uma das bordas, interna ou externa. O lado final cruza algumas das marcas do transportador, sendo essa medida o ângulo.

Pode atendê -lo: regra empírica: como aplicá -la, para que serve, exercícios resolvidos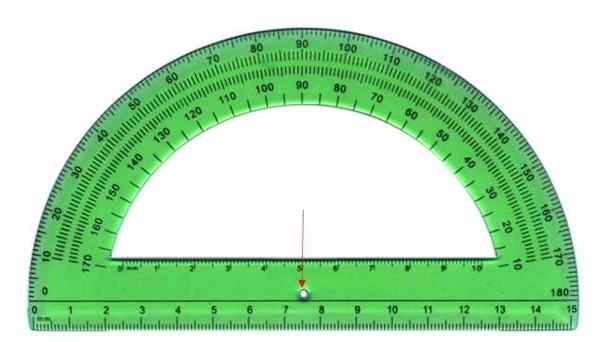O transportador é o instrumento para medir os ângulos. Fonte: Wikimedia Commons

Tipos de ângulos

Um dos critérios mais utilizados para classificar os ângulos está de acordo com sua medida. Portanto, um ângulo pode ser:

• Nulo, mede 0º.
• Afiado, cuja medida está entre 0 e 90º.
• Reto, Mede exatamente 90º.
• Obtuso, É maior que 90º e menos de 180º.
• Plano, Sua medida é igual a 180º.
• Completo, representa uma curva completa e mede 360º.

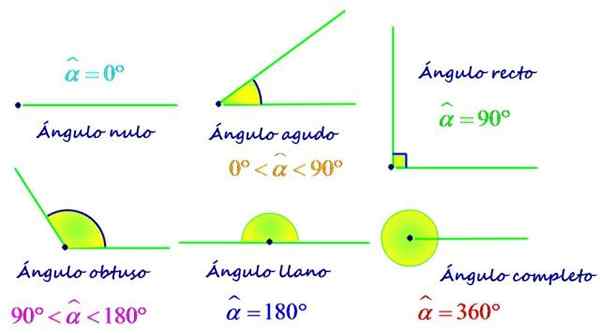Tipos de ângulos de acordo com sua medida. Fonte: f. Zapata.

De acordo com a relação entre sua medida e a do ângulo plano, que é 180º, os ângulos também podem ser classificados como:

• Côncavo, Se mede menos de 180º. Portanto, os ângulos agudos, retos e obtusos são côncavos, pois sua medida é sempre menor que 180º (veja a figura acima).
• Convexo, Se sua medida for maior que 180º, pois os ângulos de 270º e 360º.

Ângulos de acordo com a soma de suas medidas e de acordo com a posição de seus lados

Dois ângulos porte A e porte B podem ser:

• Complementar, Se a soma de suas medidas for igual a 90º.
• Suplementar, Ao adicionar as respectivas medidas, 180º é obtido.
• Conjugado, Se esta soma for igual a 360º.

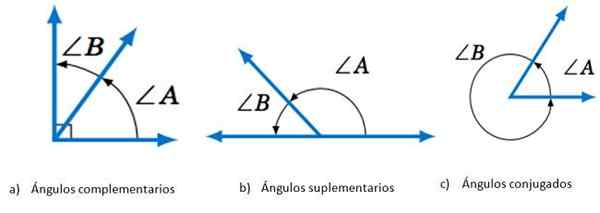Ângulos de acordo com a soma de suas medidas. Fonte: Mathematics Librettexts.

Quanto à posição de seus lados, dois ângulos podem ser:

• Em uma sequência, Quando o vértice e um dos lados têm em comum.
• Adjacente, Se eles são consecutivos, mas os lados não comuns são opostos, então eles também são suplementares.
• Oposto pelo vértice, Quando eles têm o vértice comum, e os lados dos ângulos são prolongados na direção oposta.

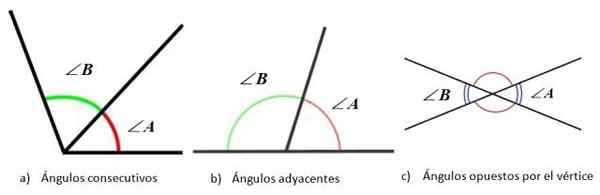Ângulos de acordo com a posição relativa entre os lados. Fonte: f. Zapata

Triângulos

O triângulo é uma figura geométrica plana e fechada, pertencente à família dos polígonos, com três lados compostos de linhas que são cortadas duas a duas, gerando três ângulos.

Pode servir a você: Função Bijectiva: O que é, como é feito, exemplos, exercícios

Seus elementos básicos são:

• Vértices, que são os pontos de interseção das linhas acima mencionadas.
• Lados, um total de 3 e isso consiste nos segmentos de linhas que se conectam aos vértices.
• Ângulos internos, Também no número de 3, cuja soma é sempre igual a 180º.

Geralmente, os lados são denotados com letras latinas minúsculas, os vértices com letras maiúsculas e os ângulos com letras minúsculas e minúsculas, mas outras notações também são possíveis.

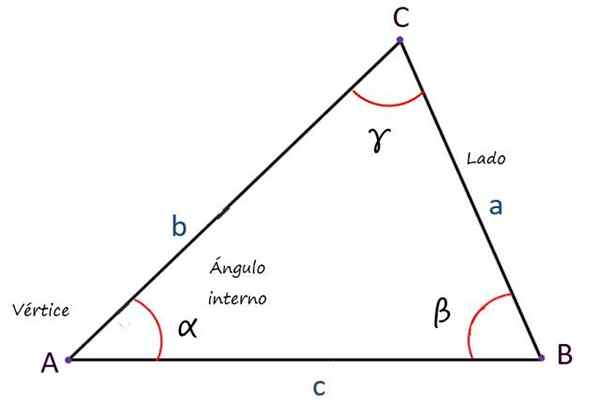Principais elementos de um triângulo. Fonte: f. Zapata

Tipos de triângulos

Triângulos de acordo com a forma de seus lados

De acordo com este critério, os triângulos podem ser:

• Equilaterais, Se seus três lados têm a mesma medida.
• Isósceles, Quando apenas dois lados têm igual medida, enquanto o terceiro é diferente.
• Escaleno, Se os três lados tiverem tamanho diferente.

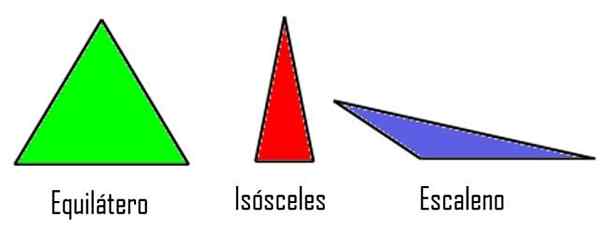Triângulos de acordo com os lados. Wikimedia modificada Commons

Triângulos de acordo com seus ângulos internos

Este critério é baseado nos tipos de ângulo interno do triângulo. De acordo com isso, um triângulo pode ser:

• Acutangle, Quando os três ângulos internos do triângulo são agudos.
• Retângulo, Se o triângulo tiver um ângulo de medida interno igual a 90º.
• Obtuso, Um dos ângulos internos do triângulo é obtuso.

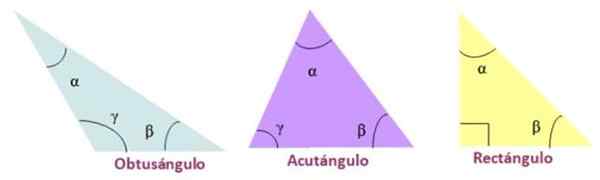Tipos de triângulo de acordo com seus ângulos internos. Fonte: f. Zapata

Segmentos de triângulo notáveis

Entre os segmentos notáveis ​​de qualquer triângulo, eles têm:

• Mediana, segmento direcionado de um vértice, diretamente para o lado oposto.
• MediaTrix, É um segmento pertencente à linha perpendicular ao lado, que se cruza para o ponto médio desse lado.
• Bissetor, segmento que divide um ângulo interno em duas partes iguais, e que se estende ao lado oposto ao ângulo.
• Altura, segmento perpendicular ao lado, que se estende ao vértice oposto.

Pode atendê -lo: interpolação de Lagrange

Três médios, três mediatrices podem ser rastreados e assim por diante.

Centros de triângulo

Em qualquer triângulo, os seguintes pontos se destacam (veja a figura a seguir):

• Baricentro g, Também às vezes chamado centróide do triângulo, é o ponto de interseção das medianas e é sempre interior ao triângulo.
• Ortocenter h, ponto em que as três alturas se cruzam.
• Circunncentro ou, É o ponto de interseção de mediatrices. Pode ser encontrado fora do triângulo, se isso for obtuso, enquanto, no triângulo retângulo, ou coincide com o ponto médio da hipotenusa.
• No centro, Ponto de interseção para bissetores de triângulo.
• Euler reto, reto que une o baricenter, o ortocentro e o circunncentro, em qualquer triângulo que não seja equilateral. É sempre cumprido que o comprimento do segmento Hg é o dobro do segmento Go.

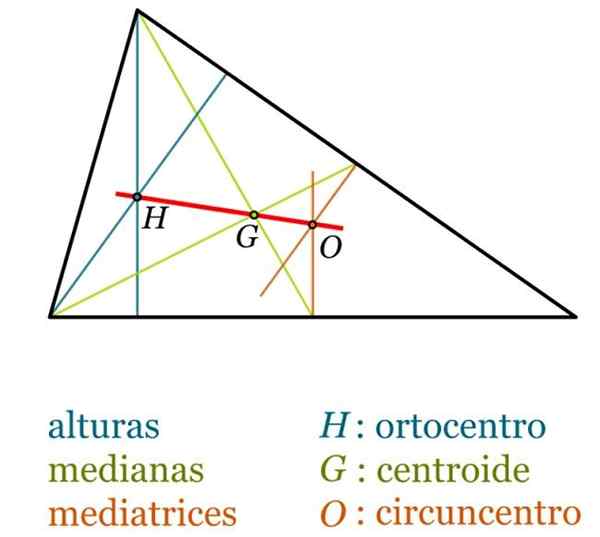Pontos notáveis ​​e segmentos do triângulo. Fonte: Wikimedia Commons

Área de um triângulo

Para calcular a área A do triângulo, a seguinte fórmula é usada, de natureza geral:

A = base × altura / 2

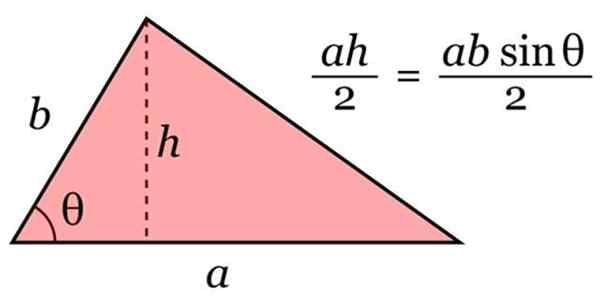Área do triângulo. Fonte: Wikimedia Commons

Fórmula Herón

Conhecendo a duração de todos os lados do triângulo, a seguinte fórmula, conhecida como Fórmula Herón, Permite que você encontre a área A:

Aqui, os lados do triângulo são A, B e C, enquanto S_p é o semi -perímetro, isto é, metade do perímetro p = a + b + c.

Referências

1. Alexander, d. 2013. Geometria. 5 ª. Edição. Cengage Learning.
2. Ângulos. Matemática Librettexts. Recuperado de: matemática.Librettexts.org.
3. Jiménez, René. 2010. Matemática II (geometria e trigonometria). 2º. Edição. Pearson.
4. Fórmulas do Universo. Triângulo. Recuperado de: universoformulas.com.
5. Zapata, f. Triângulos: história, elementos, classificação, propriedades. Recuperado de: Lifer.com.