Multiplicação de frações como é feito, exemplos, exercícios

O Multiplicação de frações É uma operação aritmética entre duas ou mais frações que dão origem a uma nova fração. Seu numerador está multiplicando os numeradores das frações participantes, e o denominador é da mesma maneira.

Vamos ver com um exemplo na imagem a seguir. Suponha que haja duas frações A/B e C/D, com B e D diferentes de 0.

figura 1. A multiplicação de frações é uma operação que é feita online. Fonte: f. Zapata.

Para realizar a multiplicação entre eles, o produto é feito entre os numeradores e também o dos denominadores. Dessa maneira.

Este procedimento é facilmente estendido à multiplicação de três e mais frações. Vamos ver mais detalhes abaixo.

Como é feita a multiplicação de frações?

O produto pode ser simbolizado com uma cruz ou com um ponto intercalado entre frações. Além disso, deve -se levar em consideração que as frações podem ter um sinal positivo ou um sinal negativo, por isso é necessário ter cuidado para seguir a regra de sinais:

-Quando dois números de sinal igual são multiplicados, o produto é positivo.

-Se duas quantidades de sinais diferentes forem multiplicadas, o resultado será negativo.

Desta maneira:

Depois que o procedimento é realizado, a fração é simplificada, se possível. Este no caso de numerador e denominador não serem primos. Por exemplo:

Se o numerador e o denominador das frações participantes não forem primos, é conveniente simplificá -las antes de fazer a multiplicação de frações. Dessa forma, números menores e mais gerenciáveis ​​são obtidos ao executar os produtos.

Pode atendê -lo: quantas soluções uma equação quadrática tem?

Propriedades das frações multiplicação

Produto por 0

Qualquer fração multiplicada por 0 é igual a 0:

Produto por 1

Qualquer fração multiplicada por 1 é igual a si mesma:

Portanto, o 1 é considerado elemento neutro de multiplicação. Observe que todo o número 1 tem uma expressão fracionária:

De tal maneira que podemos multiplicar para 1 por qualquer fração, por meio da regra já explicada. Então:

Propriedade comutativa

A multiplicação de frações é comutativa, o que significa que a ordem dos fatores não altera o produto:

Propriedade associativa

A multiplicação de frações também é associativa, podemos verificar multiplicando três frações:

Onde, como sempre, os denominadores B, D e F são diferentes de 0.

Em palavras: se vamos multiplicar três frações, podemos optar por fazer o produto dos dois primeiros e multiplicar o resultado pela terceira fração. Ou multiplique os dois últimos e seu resultado finalmente o multiplique pela primeira das frações.

Qualquer que seja a ordem escolhida, o resultado será o mesmo. Vamos verificar:

Para executar a operação, as duas primeiras frações foram multiplicadas da esquerda para a direita. O resultado foi multiplicado por sua vez pela terceira fração para obter o resultado final.

A outra alternativa é multiplicar as duas últimas frações, deixando a primeira espera. O leitor pode ver que o resultado intermediário consiste em duas frações diferentes daquelas obtidas da outra maneira. Mas o resultado final é o mesmo:

Propriedade distributiva sobre a soma

Deixe três frações A/B, C/D e E/F, com B, D e F diferentes de 0. A multiplicação é distributiva em relação à soma.

Suponha que queremos executar a seguinte operação:

A maneira de executá -lo, através desta propriedade, é a seguinte:

Pode atendê -lo: Teste de Tukey: O que é, em caso de exemplo, exercício resolvido

Portanto, o produto de um número para a soma de outros dois pode ser feito adicionando dois produtos: o primeiro para o segundo e o primeiro pelo terceiro. É muito simples por um exemplo:

O resultado final parece simplificado ao máximo, conforme explicado acima.

Exemplos

Multiplicação de uma fração por um número inteiro

Suponha que você queira multiplicar uma fração A/B por um número inteiro n:

Vimos anteriormente que o número 1 pode ser expresso como uma fração, simplesmente colocando como denominador em 1. Podemos fazer o mesmo com qualquer número inteiro n, já que dividi -lo por 1 não o altera. Então:

Por exemplo:

Exemplo 2: multiplicação de uma fração por um número misto

Um número misto ou fração mista, é aquela que tem uma parte inteira e uma parte fracionária. Para realizar o produto desse número, seja com uma fração, outro número misto ou com um número inteiro, é necessário transformá -lo por sua vez em fração.

A fração que representa um número misto é um Fração imprópria, A cujo numerador tem maior valor absoluto que o denominador.

Podemos obtê -lo através da soma de toda a parte, convenientemente expressa como uma fração colocando um 1 como denominador, mais a parte fracionária.

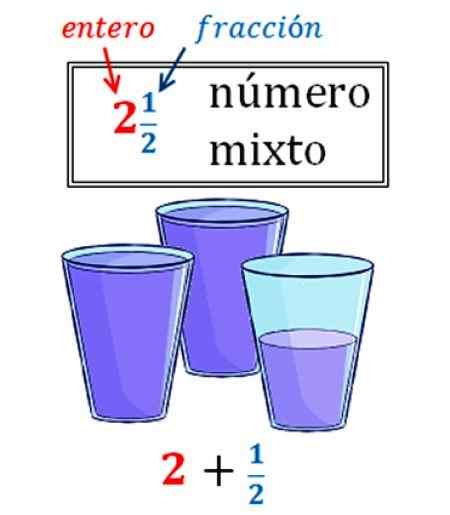Figura 2. Um número misto transformado em fração. Fonte: Wikimedia Commons.

Na imagem, há um exemplo de número misto, que demonstra a frequência. Temos 2 copos e meio de água, que como um número misto são expressos assim:

2 ½

Temos a fração inadequada que a representa:

Agora suponha que queremos encontrar as 3/4 partes de dois copos e meio de água. O que devemos fazer é multiplicar 3/4 pela fração inadequada obtida:

Pode servir a você: Distribuição de Poisson: fórmulas, equações, modelo, propriedades

Exercícios resolvidos

Exercício 1

Realize a seguinte operação:

Solução

O número 1 ¾ é um número misto. Toda a sua parte é 1 e sua parte fracionária é ¾. Se executarmos a operação: 1 + ¾, o número misto será transformado em uma fração inadequada.

1 + ¾ = (4 + 3) /4 = 7/4

Depois que o número misto da fração inadequada é transformada, a operação de multiplicação é realizada como de costume:

Exercício 2

A idade de José é ½ dos 2/3 da idade de Manuel. Se Manuel tem 24 anos, qual é a idade de José?

Solução

Deixe X a era de José, um desconhecido que devemos encontrar. A declaração nos diz que a idade de Manuel é de 24 anos, portanto esse valor é conhecido.

Para determinar a idade de José, realizamos as operações indicadas pela declaração: "A idade de José é ½ dos 2/3 da idade de Manuel".

Esta é a multiplicação de duas frações para um número inteiro:

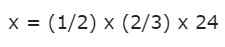
Podemos multiplicar as duas primeiras frações de acordo com as regras descritas antes. Por sua vez, o número 24 é um número inteiro, mas já sabemos que não há problema em transformá -lo em uma fração, simplesmente colocando um 1 como denominador:

Podemos simplificar bastante a operação, observando que o 2 no numerador da segunda fração é imediatamente cancelado com o 2 que é como um denominador no primeiro.

É isso que nos resta depois do cancelamento:

Portanto, José tem 8 anos.

Referências

1. Baldor, a. 1986. Aritmética. Edições e distribuições Codex.
2. Carena, m. 2019. Manual de Matemática. Universidade Nacional da Costa.
3. Jiménez, r. 2008. Álgebra. Prentice Hall.
4. Sangaku Maths. Multiplicação de frações. Recuperado de: sangakoo.com.
5. Smartick. Multiplicação de frações. Recuperado de: Smartick.é.