Método húngaro o que consiste, exemplo

Ele Método húngaro É um algoritmo usado em problemas de alocação quando você deseja minimizar o custo. Ou seja, é usado para encontrar o custo mínimo, atribuindo várias pessoas a várias atividades com base no custo mais baixo. Cada atividade deve ser atribuída a uma pessoa diferente.

Um problema de atribuição é um tipo especial de problema de programação linear, onde o objetivo é minimizar o custo ou o tempo de concluir uma quantidade de trabalho de várias pessoas.

Fonte: Pixabay.com

Uma das características importantes do problema de alocação é que apenas um trabalho (ou trabalhador) é atribuído a uma máquina (ou projeto).

Este método foi desenvolvido pelo matemático húngaro D. Konig. Por esse motivo, é conhecido como método húngaro para problemas de alocação. Também é conhecido como algoritmo de atribuição Kuhn-Munkres.

Qualquer problema de alocação pode ser resolvido facilmente aplicando este método que consiste em duas fases:

- Com a primeira fase, há reduções de linhas e reduções de coluna.

- Na segunda fase, a solução em uma base iterativa é otimizada.

[TOC]

Qual é o método húngaro?

O método húngaro consiste em quatro etapas. As duas primeiras etapas são executadas apenas uma vez, enquanto as etapas 3 e 4 são repetidas até encontrar uma atribuição ideal.

É considerado um fato de entrada para uma matriz quadrada de ordem n por n, que deve conter apenas elementos não negativos.

Para um determinado problema, se o número de linhas na matriz não for igual ao número de colunas, uma linha fictícia ou uma coluna fictícia deve ser adicionada, dependendo do caso. Os custos de atribuição para essas células fictícios são sempre atribuídos como zero.

Etapa 1: subtrair os mínimos de cada linha

Para cada linha da matriz, o elemento é selecionado com o menor valor e subtrações de cada elemento nessa linha.

Pode atendê -lo: qual é o ativo atual? (Com exemplos)

Etapa 2: subtrair os mínimos de cada coluna

Da mesma forma, o elemento com o menor valor é selecionado para cada coluna e subtraí -lo de cada elemento nessa coluna.

Etapa 3: Cubra todos os zeros com um número mínimo de linhas

Todos os zeros devem ser cobertos na matriz resultante da etapa 2 usando um número mínimo de linhas horizontais e verticais, por linhas ou colunas.

Se forem necessários linhas totais para cobrir todos os zeros, sendo N igual ao tamanho n por n da matriz, haverá uma atribuição ideal entre os zeros e, portanto, o algoritmo para.

Caso contrário, se menos linhas forem necessárias para cobrir todos os zeros na matriz, ela continua com a etapa 4.

Etapa 4: Crie zeros adicionais

O menor elemento da matriz (chamado k) é selecionado que não é coberto por uma das linhas feitas na etapa 3.

O valor de K de todos os elementos que não são cobertos por linhas é subtraído. Posteriormente, o valor de k é adicionado a todos os elementos cobertos pela interseção de duas linhas.

Os elementos cobertos por uma única linha são deixados como são. Depois de executar esta etapa, você retorna à etapa 3.

Atribuição ideal

Depois que o algoritmo é interrompido na etapa 3, um conjunto de zeros é escolhido para que cada linha e cada coluna tenha apenas um zero selecionado.

Se neste processo de seleção não houver zero em uma linha ou coluna, um desses zeros será escolhido. Os zeros restantes são eliminados nessa coluna ou linha, repetindo o mesmo para as outras tarefas também.

Pode atendê -lo: macrolocalização

Se não houver uma alocação única de zeros, significa que existem várias soluções. No entanto, o custo permanecerá o mesmo para os diferentes conjuntos de alocações.

Qualquer linha ou coluna fictícia que foi adicionada é eliminada. Os zeros escolhidos nesta matriz final correspondem à tarefa ideal necessária na matriz original.

Exemplo

Considere uma empresa em que existem quatro atividades (A1, A2, A3, A4) que devem ser executadas por quatro trabalhadores (T1, T2, T3, T4). Uma atividade por trabalhador deve ser atribuída.

A matriz a seguir mostra o custo de atribuir um determinado trabalhador a uma determinada atividade. O objetivo perseguido é minimizar o custo total da tarefa composta por essas quatro atividades.

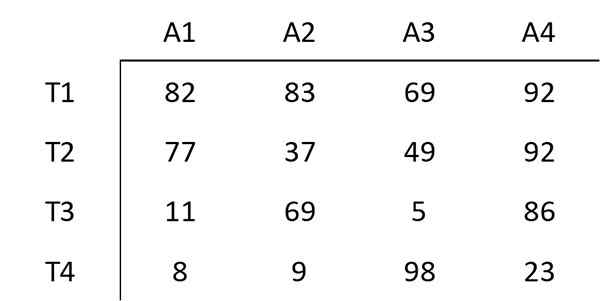
Etapa 1: subtrair os mínimos de cada linha

O elemento começa com o valor mínimo de cada linha dos outros elementos dessa linha. Por exemplo, o menor elemento na primeira linha é 69. Portanto, 69 de cada elemento são subtraídos na primeira linha. A matriz resultante é:

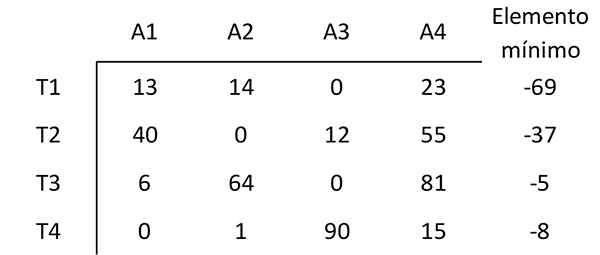
Etapa 2: subtrair os mínimos de cada coluna

Da mesma forma, o elemento é subtraído com o valor mínimo de cada coluna dos outros elementos dessa coluna, obtendo a seguinte matriz:

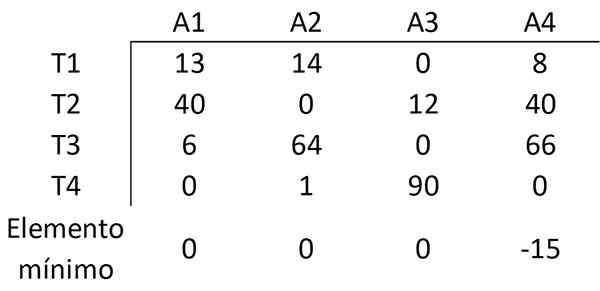
Etapa 3: Cubra todos os zeros com um número mínimo de linhas

Agora, o número mínimo de linhas (horizontal ou vertical) será determinado que são necessários para cobrir todos os zeros na matriz. Todos os zeros podem ser cobertos usando 3 linhas:

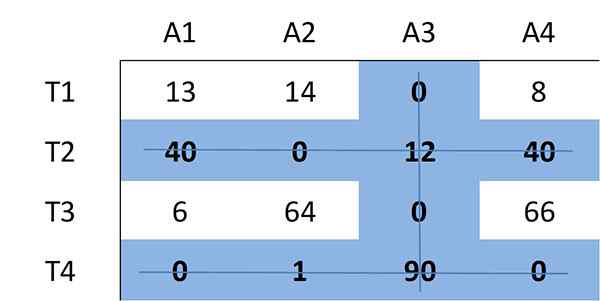
Como o número de linhas necessárias é três e é menor que o tamanho da matriz (n = 4), continua com a etapa 4.

Pode atendê -lo: Gerenciamento de projetos: o que é, fases, objetivos, exemplos

Etapa 4: Crie zeros adicionais

O elemento mais baixo não coberto pelas linhas é selecionado, cujo valor é 6. Este valor de todos os elementos não cobertos é subtraído e esse mesmo valor é adicionado a todos os elementos cobertos pela interseção de duas linhas. Isso resulta na seguinte matriz:

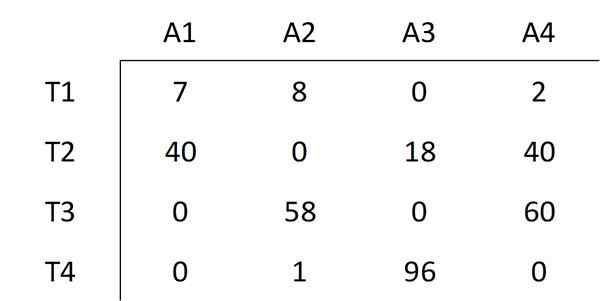
Conforme indicado no método húngaro, a etapa número três deve ser realizada novamente.

Etapa 3 (repetição)

Novamente, o número mínimo de linhas necessárias para cobrir todos os zeros na matriz é determinado. Desta vez, quatro linhas são necessárias:

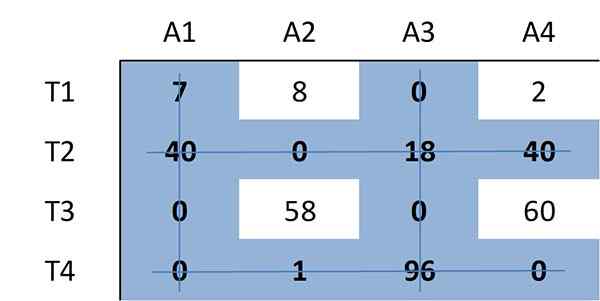
Como o número de linhas necessárias é 4, igual ao tamanho da matriz (n = 4), há uma atribuição ideal entre os zeros na matriz. Portanto, o algoritmo para.

Atribuição ideal

Conforme indicado pelo método, a seleção feita dos seguintes Zeros corresponde a uma atribuição ideal:

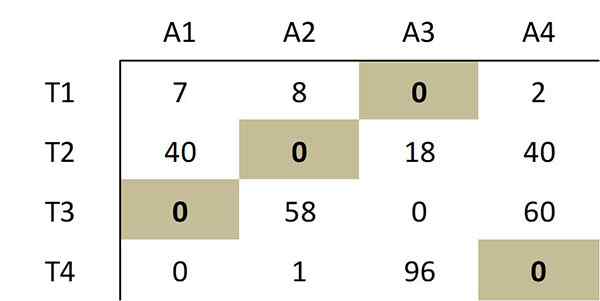
Esta seleção de Zeros corresponde à seguinte alocação ideal na matriz de custo original:

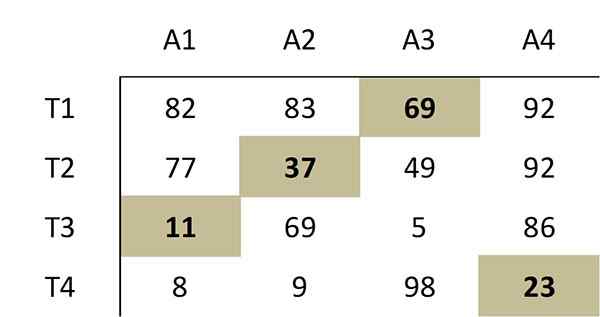
Portanto, o trabalhador 1 deve realizar a atividade 3, o trabalhador 2, a atividade 2, o trabalhador 3, a atividade 1 e o trabalhador 4 devem realizar a atividade 4. O custo total desta atribuição ideal é 69+37+11+23 = 140.

Referências

1. Algoritmo da Hungria (2019). O algoritmo da Hungria. Retirado de: HungarianalGorithm.com.
2. Estudo (2019). Usando o algoritmo da Hungria para resolver problemas de atribuição. Retirado de: Estudo.com.
3. Wisdom Jobs (2018). Hungria Método para resolver o problema de atribuição - técnicas quantitativas para gerenciamento. Retirado de: wisdomjobs.com.
4. Geeks for Geeks (2019). Algoritmo da Hungria para problema de atribuição. Retirado de: geeksforgeeks.org.
5. Karleight Moore, Nathan Landman (2019). Hungria Algoritmo máximo de correspondência. Brilhante. Tirado de: brilhante.org.