Movimento pendular

O que é movimento pendular?

Ele movimento pendular É um movimento giratório feito por um objeto mais ou menos pesado, chamado pêndulo, suspenso por uma corda ou haste leve, fixada em sua outra extremidade.

O pêndulo é conferido um impulso inicial e pode oscilar, dessa maneira o objeto descreve arcos de ida e volta. Este é o princípio da operação de relógios de pêndulo, balanços, cadeiras de balanço e METRONOMES de pêndulo, usado para marcar os tempos da música.

Pêndulo oscilando, mostrando velocidade e aceleração (Wikipedia.org)

Diz -se que, em 1581, Galileu Galilei observou o influência de uma lâmpada na catedral de Pisa, observando que, embora a amplitude da oscilação do castiçal estivesse diminuindo por causa do atrito com o ar, não a duração da duração da duração da duração da duração do ciclo.

Isso chamou a atenção de Galileu, que decidiu continuar com o estudo e determinou que o período do pêndulo não depende da massa, mas da raiz quadrada do comprimento da corda, como será visto mais tarde.

Características do movimento pendular

Um pêndulo é muito fácil de construir, pois é suficiente com um prumo pendurado em um fio de algodão e segura na outra extremidade com os dedos ou amarrá -lo a um suporte como uma unha.

Após o pequeno impulso inicial, o peso é responsável por manter o pêndulo oscilando, embora o atrito esteja diminuindo a amplitude do movimento, até que finalmente cessa.

A principal característica do movimento pendente é ser repetitivo, porque é um movimento de influência. Agora, para facilitar seu estudo, é conveniente fazer algumas simplificações para se concentrar em um modelo mais simples, chamado pêndulo simples.

O pêndulo simples

A criança no balanço pode ser modelada como um pêndulo simples

É um sistema ideal que consiste em um prumo, considerado uma massa pontual m, sujeito a uma corda de comprimento leve e não extensível eu. As características deste sistema são:

• Ter um movimento repetitivo e periódico, consistindo em ir e voltar um arco de circunferência de raio igual a l.
• Não leva em consideração o atrito.
• A amplitude do movimento é pequena (< 5º).
• O período é independente da massa m, E depende apenas do comprimento eu do pêndulo.

Pode atendê -lo: vetor resultante: cálculo, exemplos, exercícios

Fórmulas e equações

A seguir, é um simples diagrama de pêndulo, no qual duas forças agem: o peso P de magnitude mg, que é direcionada verticalmente para baixo e a tensão T Na corda. Eles não são considerados atrito.

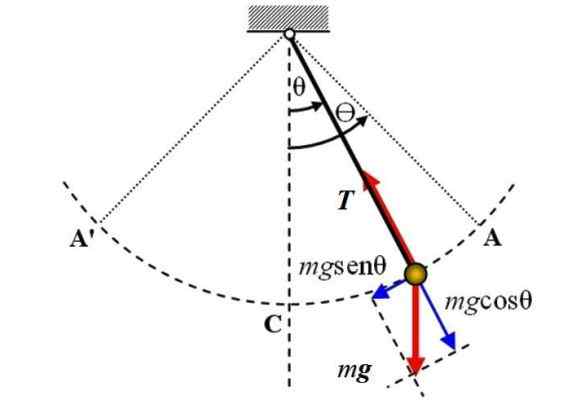Diagrama do corpo livre do pêndulo simples. Fonte: Wikimedia Commons.

O eixo de referência é o eixo vertical e coincide com a posição θ = 0, a partir daí, o deslocamento angular θ é medido, em uma direção ou outra. O sinal + pode ser atribuído à direita na figura.

Para estudar o movimento do pêndulo, um sistema de coordenadas é escolhido com a origem no próprio pêndulo. Este sistema tem uma coordenada tangencial ao arco de circunferência da A'CA descrito pelo pêndulo, bem como uma coordenada radial, direcionada para o centro da trajetória.

No momento mostrado na figura, o pêndulo está se movendo para a direita, mas o componente tangencial da gravidade, chamado f_t, é responsável por fazê -lo retornar. É avisado sobre a figura que esse componente faz sentido contrário ao movimento.

Quanto à tensão na corda, ela é equilibrada com o componente do peso mgcosθ.

A força líquida é, então, aquele chamado f_t E pela segunda lei de Newton, é igual ao produto Mass × Aceleração, E este, por sua vez, é o segundo derivado do deslocamento linear s, O que é o arco viajado pelo pêndulo. Então:

Deslocamento angular 

A equação deve ser expressa em termos de uma única variável, lembrando que o deslocamento angular θ e o arco viajado são relacionados pela equação:

Pode servir a você: Segunda Lei da Termodinâmica: Fórmulas, Equações, Exemplos

s = l.θ

A massa é cancelada de ambos os lados e, se a amplitude for pequena, o ângulo θ também, de uma maneira que a abordagem a seguir é válida:

sin θ ≈ θ

Com isso, a seguinte equação diferencial para variável θ (t) é obtida:

Esta equação é muito fácil de resolver, pois sua solução é uma função cuja segunda derivada é a própria função. Existem três alternativas: um cosseno, um peito ou um exponencial. A função cosseno é escolhida para deslocamento angular θ (t), pois é uma função bem conhecida e fácil de lidar.

O leitor pode verificar, derivando duas vezes, se a seguinte função satisfaz a equação diferencial:

θ (t) = θ_m cos (ωt + φ)

Onde θ_m É o ângulo máximo que o pêndulo se move em relação à frequência vertical e angular ω é:

A constante φ é adicionada para dar generalidade à solução e se encaixa de acordo com as condições iniciais.

Equação do período

O período T do movimento é o tempo necessário para executar um ciclo e é definido como:

Substituindo ω:

Como estabelecido anteriormente, o período não depende da massa do pêndulo, mas apenas de seu comprimento.

Exemplos de movimento pendular

Medida da frequência cardíaca

Galileu teve a ocorrência de medir a frequência cardíaca das pessoas, ajustando o comprimento do pêndulo até o período com as pulsações do coração de uma pessoa coincidem.

O relógio do pêndulo

Este é sem dúvida um dos exemplos de movimento pendular mais familiares. A fabricação de relógios Pendulum tem ciência e arte. O físico holandês Christian Huygens (1629-1695) desenvolveu o primeiro relógio Pendulum em 1656, com base no estudo feito anos atrás por Galileu.

Pode atendê -lo: Óptica ondulada

Pendulum de Foucault

Foucault Pendulum. Fonte: Wikimedia Commons.

É um pêndulo um pouco diferente do descrito acima, pois é capaz de girar em qualquer plano vertical. Foi criado pelo físico francês Léon Foucault (1819-1868) e é usado para visualizar a rotação da terra.

Exercício resolvido

Um pêndulo simples passa a cada 0.5 s para a posição de equilíbrio. Qual é a duração do fio?

Solução

Como o período é o tempo que leva para fazer um ciclo completo, no qual passa duas vezes pela posição de equilíbrio: um primeiro e o outro de volta: então:

T = 2 × 0.5 s = 1 s

De:

O comprimento l do fio é limpo:

O tópico mede 0.25 m ou 25 cm de comprimento.

Referências

1. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dinâmico. Editado por Douglas Figueroa (USB).
2. Giambattista, a. 2010. Física. 2º. Ed. McGraw Hill.
3. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed Prentice Hall.
4. Katz, d. 2013. Física para cientistas e engenheiros. Fundações e conexões. Cengage Learning.
5. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia.  Pearson.