Momento de torção

Explicamos qual é a hora da torção, suas características, fórmulas, unidades, aplicações e exercícios para resolver

Qual é a hora da torção?

Ele Momento de torção, Torque ou momento de força é a capacidade de uma força de causar uma curva. Etimologicamente, é chamado de torque como uma derivação da palavra em inglês Torque, de latim Torquere (torção).

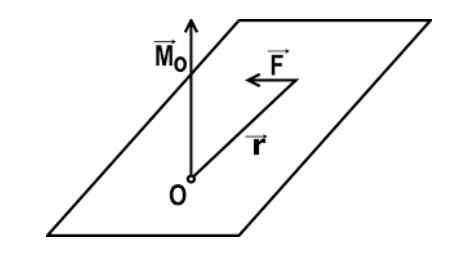
O tempo de torção (com relação a um certo ponto) é a magnitude física que resulta da execução do produto vetorial entre os vetores de posição do ponto em que a força é aplicada e a da força exercida (na ordem indicada). Este momento depende de três elementos principais.

O primeiro desses elementos é a magnitude da força aplicada, a segunda é a distância entre o ponto em que se aplica e o ponto em relação ao corpo gira (também chamado de braço da alavanca), e o terceiro elemento é a aplicação de ângulo de disse força.

Maior força, maior turno é causada. O mesmo vale para o braço da alavanca: quanto maior a distância entre o ponto em que a força e o ponto é aplicado em relação ao produzido pelo turno, maior isso será.

Logicamente, o tempo da torção é de especial interesse em construção e indústria, bem como está presente em inúmeras aplicações domésticas, como quando uma porca é espremida com uma chave em inglês.

Fórmulas

A expressão matemática do momento de torção de uma força em relação a um ponto ou é dada por: m = r x f

Nesta expressão r é o vetor que une o ponto de O com o ponto P da aplicação da força, e F é o vetor da força aplicada.

Pode atendê -lo: eletrodinâmica

As unidades de medida do momento são n ∙ m, que, embora dimensionalmente equivalentes a julho (j), têm um significado diferente e não devem ser confundidas.

Portanto, o módulo de momento de torque leva o valor dado pela seguinte expressão:

M = r ∙ f ∙ sen α

Nesta expressão, α é o ângulo entre o vetor de força e o vetor r ou o braço da alavanca. O tempo de torção é considerado positivo se o corpo girar na direção oposta às agulhas do relógio; Pelo contrário, é negativo quando se transforma em um cronograma.

Unidades

A unidade de medida da torção é o produto de uma unidade de força por uma unidade de distância. Especificamente, no sistema internacional de unidades, o metrô de Newton é usado cujo símbolo é n • m.

No nível dimensional, o metrô de Newton pode parecer equivalente a julho; No entanto, em nenhum caso deve ser usado para expressar momentos. Julho é uma unidade para medir obras ou energias que, do ponto de vista conceitual, são muito diferentes dos momentos de torção.

Da mesma forma, o momento de torção apresenta um personagem vetorial, que é o trabalho e a energia da escala.

Características do momento de torção

A partir do visto, segue -se que o momento de torção de uma força em relação a um ponto representa a capacidade de uma força ou conjunto de forças de modificar a rotação do referido corpo ao redor de um eixo que passa pelo ponto.

Portanto, o momento da torção gera uma aceleração angular no corpo e é uma magnitude de um personagem vetorial (para que seja definido de um módulo, uma direção e um sentido) que estão presentes nos mecanismos que foram submetidos a torção ou flexão.

Pode atendê -lo: Vy Canis majoris: descoberta, características, estrutura, treinamento e evolução

O tempo de torção será anulado se o vetor de força e o vetor r tiverem a mesma direção, pois nesse caso o valor de sen α será anulado.

Torque resultante

Dado um certo corpo em que uma série força age, se as forças aplicadas agirem no mesmo plano, o momento de torção resulta da aplicação de todas essas forças; É a soma dos momentos de torção como conseqüência de cada força. Portanto, é cumprido que:

M_T = ∑ m = m₁ + M_{2 +} M₃ +..

Obviamente, é necessário levar em consideração o critério de sinais para momentos de torção, conforme explicado acima.

Formulários

O torque está presente em aplicações tão todos os dias como apertar uma porca com uma chave inglesa, ou abrindo ou fechando uma torneira ou uma porta.

No entanto, seus aplicativos vão muito mais longe; O tempo de torção também é encontrado nos eixos da maquinaria ou no resultado dos esforços aos quais as vigas são submetidas. Portanto, suas aplicações na indústria e mecânica são muitas e variadas.

Exercícios resolvidos

Abaixo estão alguns exercícios para facilitar o entendimento dos acima explicados.

Exercício 1

Dada a figura a seguir em que as distâncias entre o ponto O e os pontos A e B são respectivamente 10 cm e 20 cm:

a) Calcule o valor do módulo de torque em relação ao ponto ou se uma força de 20 n é aplicada no ponto a.

b) Calcule qual deve ser o valor da força aplicada em B para alcançar o mesmo tempo de torção que foi obtido na seção anterior.

Pode atendê -lo: equação de continuidade

Solução

Primeiro, dados para unidades de sistema internacional devem passar.

r_PARA = 0,1 m

r_B = 0,2 m

a) Para calcular o momento de torção, usamos a seguinte fórmula:

M = r ∙ f ∙ sen α = 0,1 ∙ 20 ∙ 1 = 2 n ∙ m

b) Para determinar a força solicitada, prossiga de maneira semelhante:

M = r ∙ f ∙ sen α = 0,2 ∙ f ∙ 1 = 2 n ∙ m

Limpando F É obtido que:

F = 10 n

Exercício 2

Uma mulher realiza uma força de 20 N no final de uma chave inglesa de 30 cm de comprimento. Se o ângulo da força com a chave da chave for 30 °, qual é a hora da torção na porca?

Solução

A fórmula a seguir é aplicada e opera:

M = r ∙ f ∙ sen α = 0,3 ∙ 20 ∙ 0,5 = 3 n ∙ m