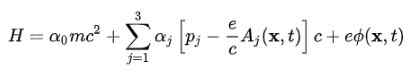Modelo Aômico de características e postulações de Dirac Jordan

Ele Modelo Atômico Dirac-Jordan É a generalização relativista do operador Hamiltoniano na equação que descreve a função de onda quântica. Ao contrário do modelo anterior, de Schrodinger, não é necessário impor a rotação pelo princípio de exclusão de Pauli, pois parece naturalmente.

Além disso, o modelo Dirac-Jordan incorpora correções relativísticas, interação com órgãos de spin e termo de Darwin, que representam a estrutura fina dos níveis eletrônicos do átomo.

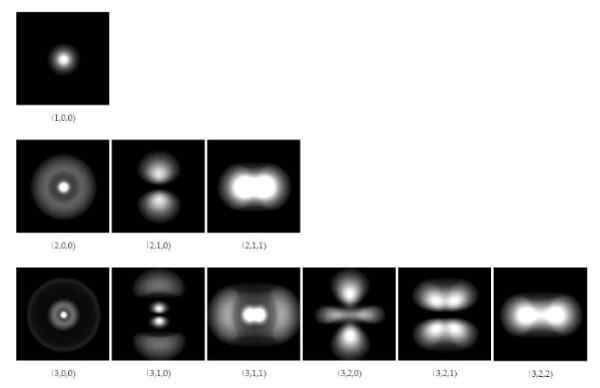
figura 1. Orbitais eletrônicos no átomo de hidrogênio para os três primeiros níveis de energia. Fonte: Wikimedia Commons.

A partir de 1928, os cientistas Paulo A. M. Dirac (1902-1984) e Pascual Jordan (1902-1980), foram propostos para generalizar a mecânica quântica desenvolvida por Schrodinger, para incluir as correções da relatividade especial de Einstein's.

Dirac parte da equação de Schrodinger, que consiste em um operador diferencial, chamado Hamiltonian, que opera em uma função conhecida como A função de onda eletrônica. No entanto, Schrodinger não levou em consideração os efeitos relativísticos.

As soluções de função de onda permitem calcular as regiões onde o elétron ao redor do núcleo será encontrado com um certo grau de probabilidade. Essas regiões ou áreas são chamadas Orbitais E eles dependem de certos números quânticos discretos, que definem a energia e o momento angular do elétron. 

[TOC]

Postulados

Em teorias mecânicas quânticas, relativísticas ou não, não há conceito de órbita, uma vez que nem a posição nem a velocidade do elétron podem ser especificadas simultaneamente. Além disso, especificar uma das variáveis ​​leva à imprecisão total no outro.

Por sua parte, Hamiltonian é um operador matemático que atua na função de onda quântica e é construída a partir da energia eletrônica. Por exemplo, um elétron livre tem energia total e isso depende de seu momento linear p desta forma:

E = (p²)/ 2m

Para construir o Hamiltoniano, ele começa a partir desta expressão e é substituído p Pelo operador quântico para o momento: 

p = -I ħ ∂ /∂r 

É importante observar que os termos p e p Eles são diferentes, já que o primeiro é o momento e o outro é o Operador diferencial associado ao momento. 

Pode atendê -lo: Modelo Atômico de Leukipo: Postula, limitações, importância

Além disso, eu sou a unidade imaginária e a constante de Planck dividida por 2π, dessa maneira o operador Hamiltoniano H do elétron livre é obtido:

H = (ħ²/2m) ∂² /∂r² 

Para encontrar o hamiltoniano do elétron no átomo, a interação eletrônica com o núcleo é adicionada: 

H = (ħ2/2m) ∂² /∂r²  - Eφ (r)

Na expressão anterior -e é a carga elétrica eletrônica e φ (r) o potencial eletrostático produzido pelo núcleo central.

Agora, o operador H atua na função de onda ψ de acordo com a equação de Schrodinger, que é escrita assim:

H ψ = (i ħ ∂ /∂t) ψ

Os quatro postulados de Dirac

Primeiro postulado: A equação da onda relativística tem a mesma estrutura que a equação de onda de Schrodinger, o que muda é H:

H ψ = (i ħ ∂ /∂t) ψ

Segundo postulado: O operador Hamiltoniano é construído com base no relacionamento de Einstein's Energy-Momentum, que é escrito assim:

E = (M² c⁴ + p² c²)^1/2

No relacionamento anterior, se a partícula tiver momento p = 0, você terá a famosa equação e = mc² que relaciona a energia de repouso de qualquer massa de massa m com a velocidade da luz C.

Terceiro postulado: Para obter o operador Hamiltoniano, é usada a mesma regra de quantização usada na equação de Schrodinger:

p = -I ħ ∂ /∂r

No começo, não estava claro como lidar com esse operador diferencial agindo dentro de uma raiz quadrada, então Dirac partiu para obter um operador hamiltoniano linear no operador do momento e a partir daí surgiu seu quarto postulado.

Postular sala: Para se livrar da raiz quadrada na fórmula de energia relativística, Dirac propôs a seguinte estrutura para e²:

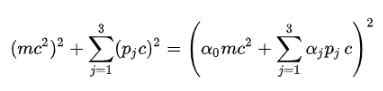
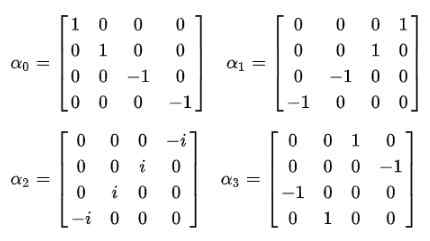
Obviamente, é necessário determinar os coeficientes alfa (α0, α1, α2, α3) para que isso seja cumprido.

A equação Dirac

A equação DIRAC foi criada pela primeira vez para o elétron livre, usando a estrutura proposta no quarto postulado. Permanece o seguinte: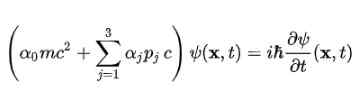

Pode atendê -lo: ouvir força: forças de superfície e massa

Em sua forma compacta, a equação Dirac é considerada uma das mais belas equações matemáticas do mundo:

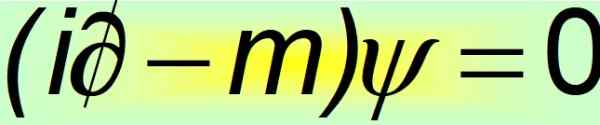Figura 2. Equação Dirac Compact. Fonte: f. Zapata.

E é quando é evidenciado que os alfas constantes não podem ser quantidades escalar. A única maneira pela qual a igualdade do quarto postulário é cumprida é que eles são matrizes constantes 4 × 4, que são conhecidas como Matrizes Dirac:

Observa -se imediatamente que a função de onda deixa de ser uma função escalar e se torna um vetor de quatro componentes Espinor:

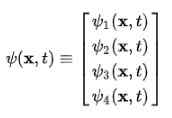
Átomo de Dirac-Jordan

Para obter o modelo atômico, é necessário passar da equação de elétrons livres para a do elétron no campo eletromagnético produzido pelo núcleo atômico. Essa interação é levada em consideração incorporando o potencial escalar φ e o vetor potencial PARA No Hamiltoniano:

A função de onda (Espinor) resulta da incorporação deste Hamiltoniano tem as seguintes características: 

- Ele cumpre a relatividade especial, pois leva em consideração a energia intrínseca do elétron (primeiro termo do hamiltoniano relativista)

- Tem quatro soluções correspondentes aos quatro componentes do Espinor

- As duas primeiras soluções correspondem a uma para girar +½ e a outra para a spin - ½ 

- Finalmente, as outras duas soluções prevêem a existência de antimateria, uma vez que correspondem à dos positrons dos opostos opostos.

A grande vantagem da equação Dirac é que as correções básicas hamiltonianas de Schrodinger H (O) podem ser divididas em vários termos que mostraremos abaixo:

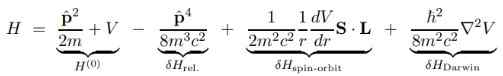
Na expressão anterior V é o escalar potencial, já que o vetor potencial PARA É nulo se for para o próton estacionário central e é por isso que não aparece.

A razão pela qual as correções de Dirac em relação às soluções de Schrodinger na função de onda são sutis. Eles surgem do fato de que os três últimos termos do Hamiltoniano corrigido são todos divididos pela velocidade C do quadrado, um número imenso, que torna esses termos numericamente pequenos.

Pode atendê -lo: Vy Canis majoris: descoberta, características, estrutura, treinamento e evolução

Correções relativísticas para o espectro de energia

Usando a equação dic-jordan, são encontradas correções no espectro de energia eletrônica no átomo de hidrogênio. Também existem correções para a energia em átomos com mais de um elétron aproximadamente através de uma metodologia conhecida como a teoria dos distúrbios.

Da mesma forma, o modelo DIRAC permite encontrar a correção da estrutura fina nos níveis de energia de hidrogênio. 

No entanto, correções ainda mais sutis, como a estrutura hiperfina e a mudança de Cordeiro, são obtidas de modelos mais avançados, como Teoria Quantum Campos, nascido precisamente devido às contribuições do modelo Dirac.

A figura a seguir mostra como as correções relativísticas da DIRAC estão nos níveis de energia:

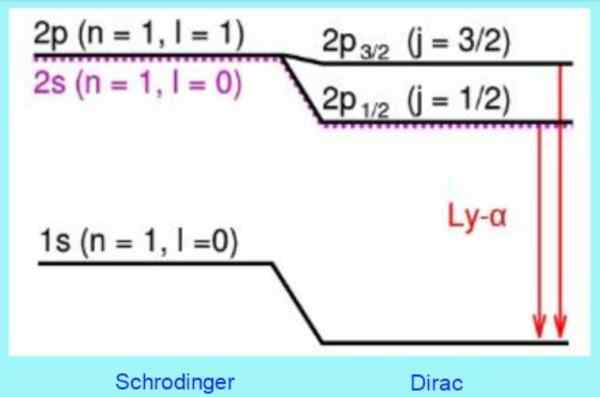Figura 3. Correções do modelo Dirac nos níveis de átomos de hidrogênio. Fonte: Wikimedia Commons.

Por exemplo, as soluções para a equação Dirac prevêem corretamente uma mudança observada no nível 2s. É a correção de estrutura fina bem conhecida na linha Lyman - alfa do espectro de hidrogênio (veja a Figura 3).

A propósito, a estrutura fina é o nome que recebe na física atômica o desdobramento das linhas do espectro de emissão dos átomos, o que é uma consequência direta do spin eletrônico.

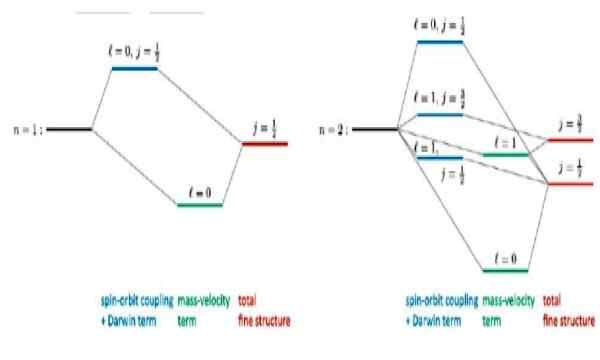Figura 4. Estrutura fina se desenrolando para o estado base n = 1 e o primeiro estado excitado n = 2 no átomo de hidrogênio. Fonte: r wirnata. Correções relativísticas para átomos semelhantes a hidrogênio. Pesquisa.líquido

Artigos de interesse

Modelo Atômico de Broglie.

Modelo Atômico de Chadwick.

Modelo Atômico de Heisenberg.

Modelo atômico de perrina.

Modelo Atômico de Thomson.

Modelo atômico de Dalton.

Modelo Atômico de Schrödinger.

Modelo Atômico do Demócrito.

Modelo Atômico de Leucipo.

Modelo atômico Bohr.

Modelo atômico atual.

Referências

1. Teoria atômica. Recuperado da Wikipedia.org.
2. Momento magnético eletrônico. Recuperado da Wikipedia.org.
3. Quanta: um manual de conceitos. (1974). imprensa da Universidade de Oxford. Recuperado da Wikipedia.org.
4. Modelo Atômico Dirac Jordan. Recuperado de Prezi.com.
5. O novo universo quântico. Cambridge University Press. Recuperado da Wikipedia.org.