Mínimos quadrados

Qual é o método de quadrados mínimos?

O método de Mínimos quadrados É uma das aplicações mais importantes na abordagem das funções. A idéia é encontrar uma curva de modo que, dado um conjunto de pares arrumados, essa função é melhor abordada para os dados. A função pode ser uma linha, uma curva quadrática, um cúbico, etc.

A idéia do método é minimizar a soma dos quadrados das diferenças nas ordenadas (componente y), entre os pontos gerados pela função escolhida e os pontos pertencentes ao conjunto de dados.

Método quadrado mínimo

Antes de dar o método, devemos primeiro ficar claros sobre o que "está se aproximando melhor". Suponha que seja procurada uma linha y = b+mx, que é melhor representar um conjunto de n pontos, a saber (x1, y1), (x2, y2)…, (xn, yn).

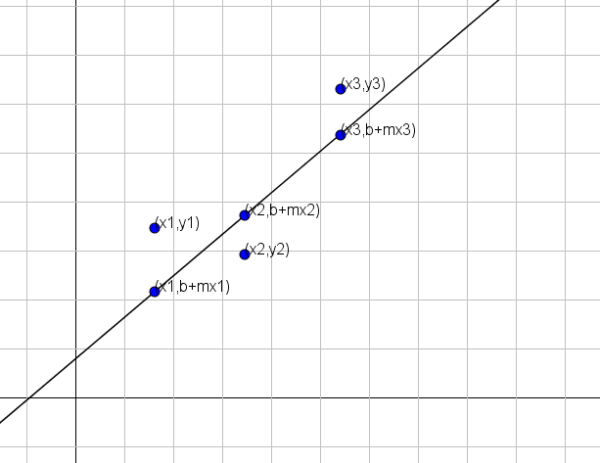
Como mostrado na figura anterior, se as variáveis ​​x e y foram relacionadas pela linha y = b+mx, então para x = x1 o valor correspondente de y seria b+mx1. No entanto, esse valor é diferente do valor verdadeiro de y, que é y = y1.

Lembre -se de que no avião, a distância entre dois pontos é dada pela seguinte fórmula:

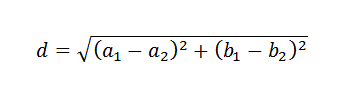
Com isso em mente, para determinar como escolher a linha y = b+mx que melhor se aproxima dos dados fornecidos, parece lógico usar como critério a seleção da linha que minimiza a soma dos quadrados das distâncias entre os pontos e a linha.

Como a distância entre os pontos (x1, y1) e (x1, b+mx1) é y1- (b+mx1), nosso problema é reduzido a encontrar números M e B, de modo que a próxima soma seja mínima:

Pode servir a você: teorema verde, demonstração, aplicações e exercícios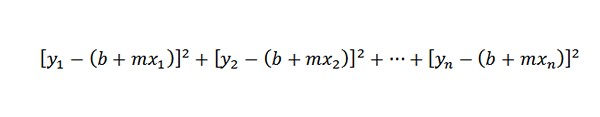

A linha que atende a essa condição é conhecida como "abordagem da linha de quadrados mínimos para os pontos (x1, y1), (x2, y2), ..., (xn, yn)".

Uma vez que o problema é obtido, resta apenas um método para encontrar a abordagem por quadrados mínimos. Se os pontos (x1, y1), (x2, y2), ..., (xn, yn) estiverem todos na linha y = mx+b, teríamos que ser colineais e:

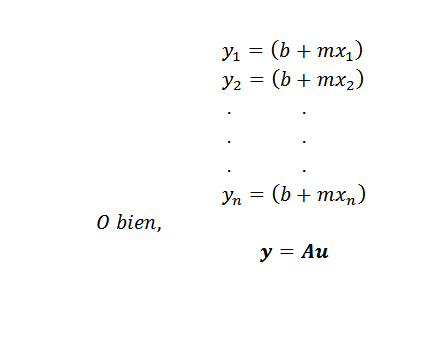
Nesta expressão:

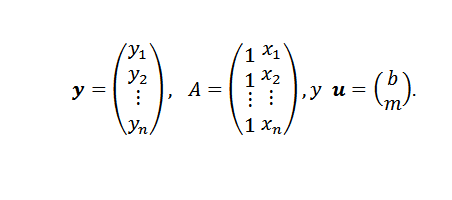
Finalmente, se os pontos não forem colineares, então y-Au = 0 e o problema pode se traduzir em encontrar um vetor ou que o padrão euclidiano seja mínimo.

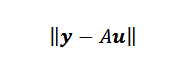
Encontrar o vetor minimizante ou não é tão difícil quanto você pode pensar. Como A é uma matriz nx2 e u é uma matriz 2 × 1, temos que o vetor AU é um vetor em rⁿ e pertence à imagem de A, que é um subespaço de Rⁿ Com uma dimensão não mais que dois.

Vamos assumir que n = 3 para mostrar qual é o procedimento que deve ser seguido. Se n = 3, a imagem de A será um avião ou uma linha que passa pela origem.

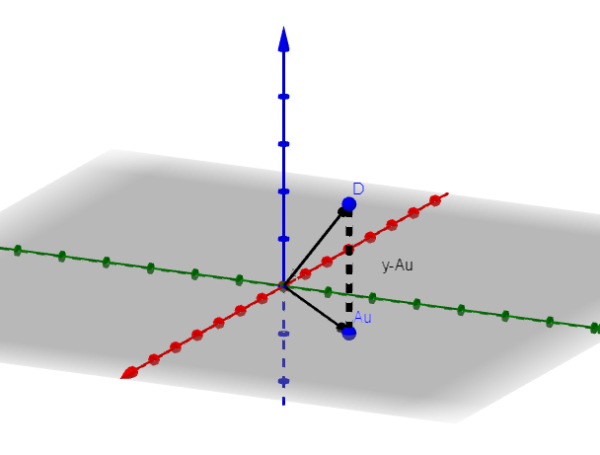
Deixe V o vetor de minimização. Na figura, observamos que Y-Au é minimizado quando é ortogonal à imagem de um. Ou seja, se V é o vetor minimizador, acontece que:

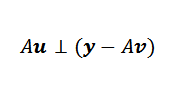
Então, podemos expressar o exposto dessa maneira:

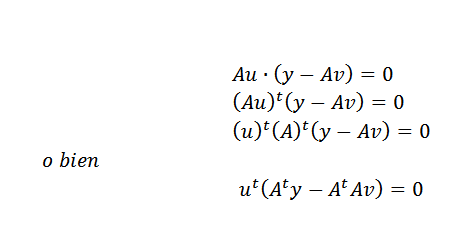
Isso só pode acontecer se:

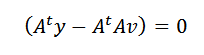
Finalmente, limpando v, temos que:

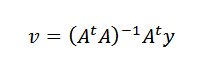
É possível fazer isso desde^tA é invertível sempre que os n pontos como dados não são colineais.

Agora, se, em vez de procurar uma linha, desejamos encontrar uma parábola (cuja expressão seria da forma y = a+bx+cx²) Que foi uma aproximação melhor aos pontos de dados, o procedimento seria descrito abaixo.

Pode atendê -lo: números inteiros

Se os pontos de dados estivessem nessa parábola, teria que::

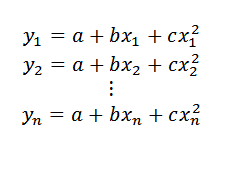
Então:

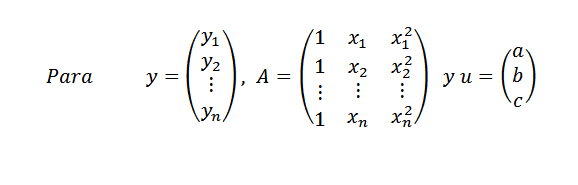
Da mesma forma, podemos escrever y = au. Se todos os pontos não estiverem na parábola, temos que Y-Au é diferente de zero para qualquer vetor u e nosso problema é novamente: encontre um vetor u em r3, de modo que seja a norma || y-ua || seja o máximo possível.

Repetindo o procedimento anterior, podemos chegar ao vetor procurado é:

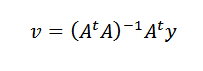
Exercícios resolvidos

Exercício 1

Encontre a linha que melhor se adequa aos pontos (1.4), (-2,5), (3, -1) e (4.1).

Solução

Temos que:

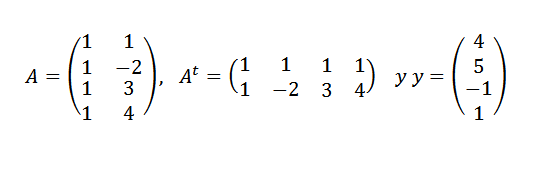
Então:

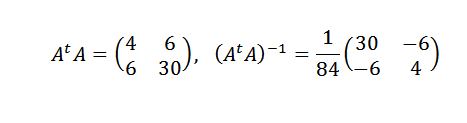
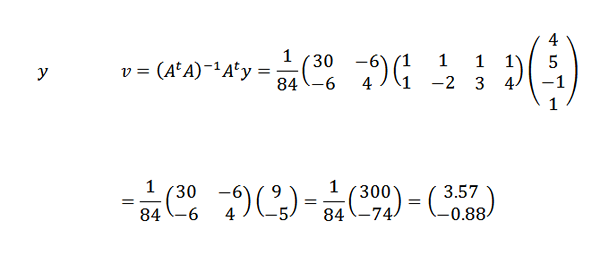
Portanto, concluímos que a linha que melhor se adequa aos pontos é dada por:

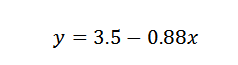
Exercício 2

Suponha que um objeto seja retirado de uma altura de 200 m. Enquanto caem, as seguintes medidas são tomadas:

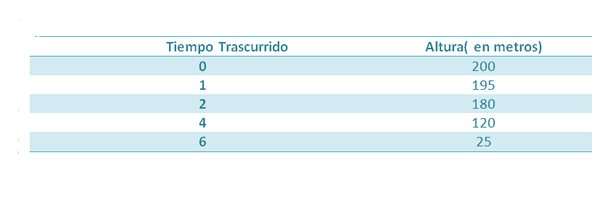
Sabemos que a altura desse objeto, após um tempo decorrida, é dada por:

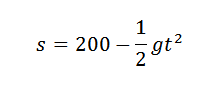
Se desejarmos obter o valor de G, podemos procurar uma parábola que seja uma abordagem melhor para os cinco pontos dados na tabela e, portanto, teríamos o coeficiente que acompanha T² Será uma abordagem razoável para (-1/2) g se as medidas forem exatas.

Temos que:

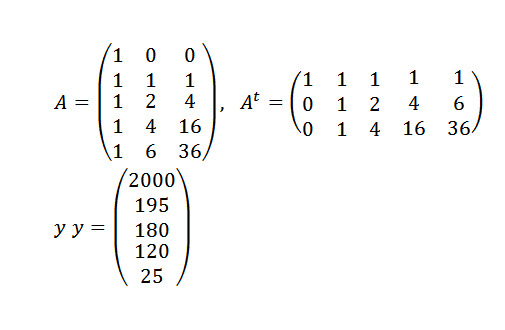
E logo:

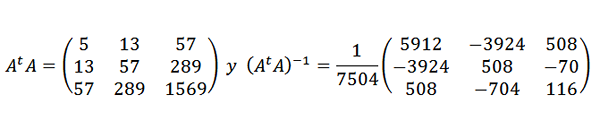
Portanto, os pontos de dados são ajustados pela seguinte expressão quadrática:

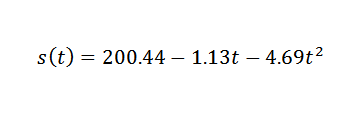
Então você tem que:

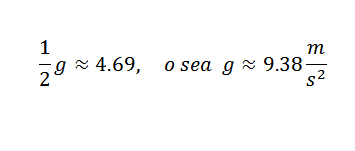
Este é um valor razoavelmente próximo do correto, que é g = 9,81 m/s². Para obter um g mais preciso de g, seria necessário começar de observações mais precisas.

Qual é o método mínimo quadrado para?

Nos problemas que ocorrem em ciências naturais ou sociais, é conveniente escrever as relações entre diferentes variáveis ​​através de alguma expressão matemática.

Pode atendê -lo: variação proporcional

Por exemplo, podemos nos relacionar na economia o custo (c), renda (i) e lucros (u) através de uma fórmula simples:

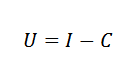
Na física, podemos relacionar a aceleração causada pela gravidade, o tempo em que um objeto está caindo e a altura do objeto por lei:

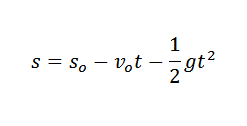
Na expressão anterior s_qualquer É a altura inicial do referido objeto e V_qualquer é sua velocidade inicial.

No entanto, encontrar fórmulas como essas não é uma tarefa simples; Geralmente corresponde ao profissional de plantão de trabalhar com muitos dados e realizar várias experiências (para verificar se os resultados obtidos são constantes) para encontrar relacionamentos entre os diferentes dados.

Uma maneira comum de conseguir isso é representar os dados obtidos em um plano como pontos e buscar uma função contínua que se aproxima de maneira ideal desses pontos.

Uma das maneiras de encontrar a função que "se aproxima" dos dados fornecidos é pelo método dos mínimos quadrados.

Além disso, como também vimos no exercício, graças a esse método, podemos obter abordagens bastante próximas às constantes físicas.