Média ponderada como é calculado, exemplos e exercícios

O média ponderada ou média aritmética ponderada, é uma medida de tendência central na qual, para cada valor x_Yo que pode levar uma variável x, um peso p é atribuído_Yo. Como resultado, denotando a média ponderada por x_p, se tem:

Com a soma da soma, a fórmula para a média ponderada é:

Onde n representa a quantidade de valores escolhidos de variável x.

O p_Yo, que também é chamado fator de ponderação, É uma medida da importância que o pesquisador atribui a cada valor. Esse fator é arbitrário e sempre positivo.

Nisso que a média ponderada difere da média aritmética simples, porque nisso, cada um dos valores x_n Tem igual significado. No entanto, em inúmeras aplicações, o pesquisador considera que alguns valores são mais importantes que outros e atribuirão um peso de acordo com seus critérios.

Aqui está o exemplo mais conhecido: suponha que um aluno apresente n avaliações em um assunto e todos tenham o mesmo peso na nota final. Nesse caso, para calcular a nota final, será suficiente para fazer uma média simples, ou seja, adicione todas as qualificações e dividir o resultado por n.

Mas se cada atividade tiver um peso diferente, porque alguns avaliam conteúdo mais importante ou mais complexo, será necessário multiplicar cada avaliação por seu respectivo peso e depois adicionar os resultados para obter a classificação final. Veremos como realizar este procedimento na seção de exercícios resolvidos.

[TOC]

Exemplos

figura 1. A média ponderada é aplicada ao calcular o índice de preços ao consumidor, um indicador de inflação. Fonte: pxhere.

O exemplo das qualificações descritas acima é uma das mais típicas em termos de aplicação da média ponderada. Outra aplicação muito importante na economia é o índice de Preços ao Consumidor qualquer Índice de preços do consumidor IPC, também chamado cesta de família e isso serve como avaliador de inflação em uma economia.

Pode atendê -lo: ângulos e triângulos

Em sua elaboração, uma série de itens é levada em consideração, como alimentos e bebidas não alcoólicas, roupas e calçados, medicamentos, transporte, comunicações, educação, lazer e outros bens e serviços.

Especialistas atribuem a cada campo um fator de ponderação, de acordo com sua importância na vida das pessoas. Os preços são coletados por um período de tempo estabelecido e, com todas as informações, o IPC desse período é calculado, que pode ser mensal, bimestral, semestral ou anual, por exemplo.

O centro de massa de um sistema de partículas

Na física, a média ponderada tem uma aplicação importante, que é calcular O centro de massa de um sistema de partículas. Esse conceito é muito útil ao trabalhar com um corpo estendido, no qual sua geometria deve ser levada em consideração.

O centro de massa é definido como o ponto em que toda a massa de um objeto estendida está concentrado. Nesse ponto, as forças podem ser aplicadas como peso, por exemplo, e assim explicar seus movimentos de tradução e rotação, através das mesmas técnicas com as quais eles trabalharam quando todos os objetos deveriam ser partículas.

Por simplicidade, começa a assumir que o corpo estendido é composto por uma quantidade N de partículas, cada uma delas com massa m e sua própria localização no espaço: o ponto de coordenada (x_Yo, e_Yo, z_Yo).

Ser x_Cm A coordenada x Do CM Downtown, então:

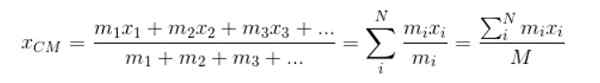
M representa a massa total do sistema. Prossegue da mesma maneira para encontrar as coordenadas e_Cm e z_Cm:

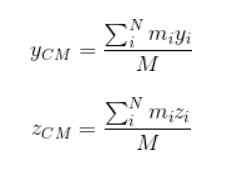
O fator de ponderação neste caso é a massa de cada uma das partículas que constituem o objeto estendido.

Pode atendê -lo: funções transcendentes: tipos, definição, propriedades, exemplos

Características importantes do centro de massa

Quando o número de partículas é muito grande, é um objeto contínuo. Nesse caso, n → ∞ e a soma é substituída por uma integral definida, cujos limites são dados pelo tamanho do objeto.

É importante destacar o fato de que não há necessariamente massa na localização do centro de massa. Por exemplo, em uma rosquinha, o centro de massa coincide mais ou menos com o centro geométrico do Rosquilla.

Figura 2. O centro de massa de uma rosquinha, um objeto bastante simétrico, está no buraco. Fonte: Pixabay.

A localização do centro de massa não depende do sistema de referência usado para estabelecer as posições das partículas, pois é uma propriedade que depende da própria configuração de objeto e não como é vista de vários quadros de referência.

Exercícios resolvidos

- Exercício 1

Em muitos casos, os professores atribuem pesos ou porcentagens diferentes a cada atividade de avaliação em sua cadeira. Assim, por exemplo, as tarefas têm uma porcentagem, os outros exames diferentes e o exame final -do ano provavelmente muito maior.

Figura 3. Em seus planos de avaliação, os professores geralmente atribuem pesos diferentes às avaliações. Fonte: Livro de Grade de David Mulder através do Flickr.

Suponha que em um determinado assunto, as atividades de avaliação e seus respectivos pesos sejam os seguintes:

-Tarefas da casa: 20 %

-Exames curtos: 25 %

-Relatórios de laboratório: 25 %

-Exame final: 30 %

a) Como o professor calcula a nota final deste assunto para cada aluno?

b) Suponha que as qualificações de um determinado aluno estejam, na escala de 1 a 5, o seguinte:

-Tarefas: 5.0 pontos

-Exames curtos: 4.7 pontos

-Relatórios de laboratório: 4.2 pontos

-Exame final: 3.5 pontos

Pode atendê -lo: Enegon: Propriedades, como fazer um Enegon, exemplos

Encontre a nota final do aluno nesta disciplina.

Solução

a) Cada avaliação tem um peso diferente, que o professor atribuiu de acordo com sua complexidade e seus próprios critérios. Dessa forma, a classificação final é calculada diretamente como:

Definitivo = (x20 % de tarefas + exames curtos x25 % + relatórios x25 % + exame final x30 %) / 100

b) Definitivo = (5.0 x 0.2) + (4.7 x 0.25) + (4.2 x 0.25) + (3.5 x 0.3) pontos = 4.275 pontos ≈ 4.3 pontos

- Exercício 2

Os proprietários de uma loja de roupas compraram jeans de três fornecedores diferentes.

O primeiro vendeu 12 unidades a um preço de € 15 cada, as segundas 20 unidades a 12.€ 80 cada e um terceiro comprado muito de 80 unidades às 11.€ 50.

Qual é o preço médio pago pelos donos da loja para cada cowboy?

Solução

x_p = (12 x 15 + 20 x 12.80 +80 x 11.50) / (12+20+80) € = 12.11 €

O valor de cada cowboy é 12.11 €, independentemente disso, alguns custam um pouco mais e outros um pouco menos. Teria sido exatamente o mesmo se os proprietários da loja tivessem comprado o 112 jeans de um único fornecedor que os teria vendido em 12.11 € a peça.

Referências

1. Arvelo, a. Medidas de tendência central. Recuperado de: Franarvelo.WordPress.com
2. Mendenhall, w. 1981. Estatística para administração e economia. 3º. edição. Grupo editorial da Iberoamerica.
3. Moore, d. 2005. Estatísticas básicas aplicadas. 2º. Edição.
4. TRIOLA, m. 2012. Estatísticas elementares. 11º. Ed. Pearson Education.
5. Wikipedia. Média ponderada. Recuperado de: em.Wikipedia.org