Limites trigonométricos como resolvê -los, exercícios resolvidos

O Limites trigonométricos São limites de funções, de modo que essas funções sejam formadas por funções trigonométricas.

Existem duas definições que devem ser conhecidas por entender como o cálculo de um limite trigonométrico é realizado. Essas definições são:

- Limite de uma função "f" quando "x" tende a "b": consiste em calcular o valor no qual f (x) se aproxima como "x" se aproxima "b", sem afirmar "b".

- Funções trigonométricas: As funções trigonométricas são as funções senoidal, cosseno e tangente, indicadas pelo pecado (x), cos (x) e bronzeado (x), respectivamente, respectivamente.

As outras funções trigonométricas são obtidas das três funções mencionadas acima.

Funções limites

Para esclarecer o conceito de um limite de função, continuaremos a mostrar alguns exemplos com funções simples.

- O limite de f (x) = 3 quando "x" tende a "8" é igual a "3", pois a função é sempre constante. Não importa quanto "x" vale, o valor de f (x) sempre será "3".

- O limite de f (x) = x-2 quando "x" tende a "6" é "4". Desde quando "X" está próximo de "6", então "X-2" se aproxima "6-2 = 4".

- O limite de g (x) = x² quando "x" tende a "3" é igual a 9, pois quando "x" está se aproximando "3" então "x²" está se aproximando "3² = 9".

Como pode ser observado nos exemplos anteriores, o cálculo de um limite consiste em avaliar o valor ao qual "x" tende na função, e o resultado será o valor do limite, embora isso seja verdade apenas para funções contínuas.

Existem limites mais complicados?

A resposta é sim. Os exemplos anteriores são os exemplos mais simples de limites. Nos livros de cálculo, os principais exercícios limitados são aqueles que geram uma indeterminação do tipo 0/0, ∞/∞, ∞ -∞, 0*∞, (1)^∞, (0)^0 e (∞)^0.

Pode servir a você: identidades pitagóricas: demonstração, exemplo, exercícios

Essas expressões são chamadas de indeterminação, pois são expressões que matematicamente fazem sentido.

Além disso, dependendo das funções envolvidas no limite original, o resultado obtido ao resolver as indeterminações pode ser diferente em cada caso.

Exemplos de limites trigonométricos simples

Para resolver limites, é sempre muito útil conhecer os gráficos das funções envolvidas. Abaixo estão os gráficos dos seios, cosseno e funções tangentes.

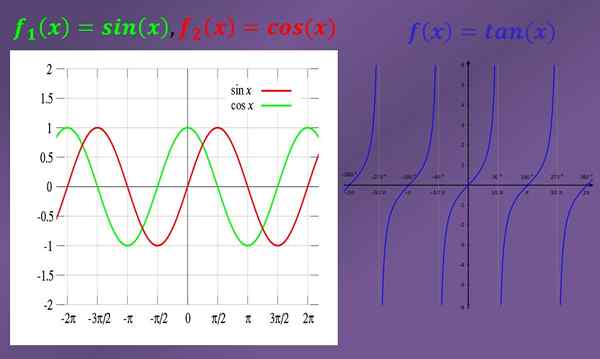
Alguns exemplos de limites trigonométricos simples são:

- Calcule o limite sem (x) quando "x" tende a "0".

Vendo o gráfico, você pode ver que se "X" estiver se aproximando "0" (tanto à esquerda quanto à direita), o gráfico do peito também está se aproximando "0". Portanto, o limite do pecado (x) quando "x" tende a "0" é "0".

- Calcule o limite de cos (x) quando "x" tende a "0".

Observando o gráfico do cosseno, pode -se observar que quando "x" está próximo de "0", o gráfico do cosseno está próximo de "1". Isso implica que o limite de cos (x) quando "x" tende a "0" é igual a "1".

Pode existir um limite (sendo um número), como é o caso nos exemplos anteriores, mas também pode acontecer que ele não existe como mostrado no exemplo a seguir.

- O limite de tan (x) quando "x" tende a "π/2" à esquerda é igual a "+∞", como pode ser visto nos gráficos. Por outro lado, o limite de tan (x) quando "x" tende a "-π/2" à direita é igual a "-∞".

Identidades de limites trigonométricos

Duas identidades muito úteis quando os limites trigonométricos estão sendo calculados são:

Pode atendê -lo: programação não linear: métodos e exercícios

- O limite de "sin (x)/x" quando "x" tende a "0" é igual a "1".

- O limite de "(1-Cos (x))/x" quando "x" tende a "0" é igual a "0".

Essas identidades são usadas com muita frequência quando você tem algum tipo de indeterminação.

Exercícios resolvidos

Resolva os seguintes limites usando as identidades descritas acima.

- Exercício 1

Calcule o limite de "f (x) = sem (3x)/x" quando "x" tende a "0".

Se a função "f" for avaliada em "0", uma indeterminação do tipo 0/0 será obtida. Portanto, devemos tentar resolver essa indeterminação usando as identidades descritas.

A única diferença entre esse limite e identidade é o número 3 que aparece na função seno. Para aplicar a identidade, a função "f (x)" deve ser reescrita da seguinte forma "3*(sem (3x)/3x)". Agora, tanto o argumento da mama quanto o denominador são iguais.

Então, quando "X" tende a "0", usando a identidade é "3*1 = 3". Portanto, o limite de f (x) quando "x" tende a "0" é igual a "3".

- Exercício 2

Calcule o limite de "g (x) = 1/x - cos (x)/x" quando "x" tende a "0".

Quando “x = 0” é substituído em g (x) uma indeterminação do tipo ∞ -∞. Para resolvê-lo, as frações são subtraídas, o que fornece como resultado "(1-Cos (x))/x".

Agora, aplicando a segunda identidade trigonométrica, o limite de g (x) é que "x" tende a "0" é igual a 0.

- Exercício 3

Calcule o limite de "h (x) = 4tan (5x)/5x" quando "x" tende a "0".

Novamente se h (x) for avaliado em "0", uma indeterminação do tipo 0/0 será obtida.

Reescrevendo como (5x) como sem (5x)/cos (5x) Acontece que h (x) = (sem (5x)/5x)*(4/cos (x))).

Pode servir a você: ângulo inscrito de um círculo: definição, teoremas, exemplos

Usando que o limite de 4/cos (x) quando "x" tende a "0" é igual a "4/1 = 4" e a primeira identidade trigonométrica é obtida que o limite de H (x) quando "x" tende "0" é igual a "1*4 = 4".

Observação

Os limites trigonométricos nem sempre são fáceis de resolver. Neste artigo, apenas exemplos básicos foram mostrados.

Referências

1. Fleming, w., & Varberg, D. E. (1989). Matemática do Pré -Eleno. Prentice Hall Ptr.
2. Fleming, w., & Varberg, D. E. (1989). Matemática pré-calculus: uma abordagem de solução de problemas (2, ilustrado Ed.). Michigan: Prentice Hall.
3. Fleming, w., & Varberg, D. (1991). Álgebra e trigonometria com geometria analítica. Pearson Education.
4. Larson, r. (2010). Pré -clulus (8 ed.). Cengage Learning.
5. Leal, j. M., & Viloria, n. G. (2005). Geometria analítica plana. Mérida - Venezuela: editorial venezuelano C. PARA.
6. Pérez, c. D. (2006). Pré -qualculus. Pearson Education.
7. Purcell, e. J., Varberg, d., & Rigdon, S. E. (2007). Cálculo (Nono ed.). Prentice Hall.
8. Saenz, J. (2005). Cálculo diferencial com funções transcendentes precoces para ciência e engenharia (Segunda edição Ed.). Hipotenusa.
9. Scott, c. PARA. (2009). Geometria plana cartesiana, Parte: Analytical Conics (1907) (Reimpressão Ed.). Fonte de raios.
10. Sullivan, m. (1997). Pré -qualculus. Pearson Education.