Leis de Morgan

Nós explicamos o que são as leis de Morgan, demonstramos e colocamos exemplos

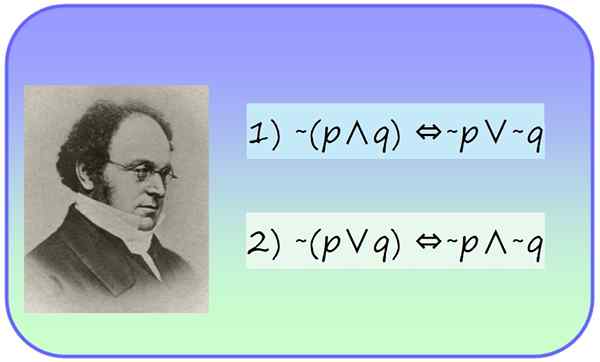figura 1.- O matemático Augustus de Morgan (1806-1871) e suas leis da lógica proposicional. Fonte: f. Zapata.

Quais são as leis de De Morgan?

As leis de De Morgan são duas leis lógicas pertencentes à lógica proposicional que foram formuladas pelo matemático inglês Augustus de Morgan (1806-1871). Eles estabelecem o seguinte, com relação a uma proposta lógica composta:

1. O oposto de uma conjunção é equivalente à disjunção que é formada com os opostos ou negações das propostas que compõem a conjunção.
2. A negação da disjunção pode ser expressa como uma conjunção composta pelos opostos ou negações das proposições envolvidas na disjunção.

Na notação de lógica proposicional, as leis de De Morgan são expressas de uma maneira compacta e mais formal como esta:

1. ∼ (p ∧ q) ⇔ ∼p ∨q
2. ∼ (p ∨ q) ⇔ ∼p ∧q

O que essas leis expressam é que, na negação de conjunção ou disjunção, o resultado é equivalente a negar a cada uma das proposições participantes separadamente e investir o conector que as vincula.

Para uma melhor compreensão das leis de De Morgan, é necessário revisar o significado das proposições e símbolos usados ​​na lógica proposicional, para ver como essas leis se aplicam convenientemente.

Notação lógica

A ferramenta básica da lógica proposicional é as proposições. Uma proposta lógica é uma declaração que admite um valor real, Se é verdadeiro ou falso, mas não ambos ao mesmo tempo. Neste não é permitido ambiguidade, ou seja, não há dúvida.

Uma proposição é indicada com uma minúscula, como nos seguintes exemplos:

• P: Cidade do México é a capital do México (verdadeiro).
• P: Ao adicionar 2 e 3, 4 (falso) é obtido.
• A: Todos os mamíferos são animais terrestres (falsos).

Pode servir você: heptagon

Também existem proposições mais complexas, estruturadas através do uso de proposições simples, como estas:

• P: Carlos irá ao cinema se não chover.
• P: ANA é um químico ou biólogo marítimo.
• R: Juan vai jantar ou Pedro verá o jogo na televisão.

Conectores lógicos

Os conectores lógicos são símbolos usados ​​para vincular proposições simples e, assim, criar proposições mais complexas. Na lógica proposicional, cada um deles tem um significado particular.

Os conectores mais utilizados são conjunção, disjunção, disjunção exclusiva, negação, condicionalidade e bi-condicionalidade.

Conjunção

A conjunção é indicada com uma carta "V" invertida. Uma proposta composta através de uma conjunção é simbolizada P ∧ q, como segue:

• P ∧ Q: Cidade do México é a capital do México e está na América do Norte.

É fácil identificar aqui que P é "Cidade do México é a capital do México" e Q is "está na América do Norte".

Disjunção

Dois tipos de disjunção são distinguidos: o fraco e o exclusivo. A Disjunção fraca É simbolizado por ∨ e na notação lógica, seria p ∨ q. Exemplo desse tipo de disjunção é:

• P ∨ P: Juan é jogador de futebol ou Juan é um tenista.

Em vez disso, o Disjunção exclusiva É simbolizado pelo sinal ⊻ e implica que uma das proposições deve ser descartada, por exemplo:

P ⊻ Q: Alicia tem 20 anos ou Alicia tem 22 anos.

A diferença entre os dois tipos é clara, em disjunção exclusiva, uma das proposições é descartada, pois se Alicia tiver 20 anos, ele não pode ter 22 anos e vice -versa. Por outro lado, na fraca disjunção, Juan pode ser jogador de futebol e tenista ao mesmo tempo.

Negação

Ao colocar o símbolo ∼ uma proposição, isso é negado, como em:

• P: ∼ (Veracruz é a capital do México).

Que é lido como "Veracruz não é a capital do México". Outras maneiras de expressar uma negação, além de "não", são através de frases como "é falso", "é uma mentira que" e "não é verdade que".

Pode atendê -lo: interpolação linear

Condicionalmente

São proposições compostas que geralmente usam as palavras "sim" e "então ..." para vincular duas proposições nas quais há condicionalidade ou implicação. A parte da proposição que é escrita imediatamente após o "sim" é o antecedente aceno hipótese da proposição e o que é depois do termo "então" é o conclusão qualquer conseqüente.

O símbolo usado para condicionalidade é a seta da esquerda para a direita "→", portanto, uma condicionalidade entre duas proposições é representada como p → q, que pode ser lida como "se p, então q". Por exemplo:

P → Q: Se chover durante a tarde, então não vou jogar tênis.

Bi-condicionalidade

Nesse tipo de proposição, a frase “sim, e somente se” para conectar duas proposições, chamado primeiro e segundo membro da Bicondicional é usado. O símbolo usado é a seta bidirecional "↔".

As duas proposições conectadas através de "sim, e somente se" são chamadas respectivamente primeiro e segundo membro e a bi-condicionalidade de duas proposições P e Q permanece como P ↔ q. Por exemplo:

P ↔ P: Maria gosta de andar de bicicleta se e somente se o dia estiver ensolarado.

Demonstração das leis de De Morgan

As leis de De Morgan fazem parte de equivalências lógicas e podem ser demonstradas através das tabelas da verdade, que são usadas para saber a verdade (verdadeira ou falsa) valor de uma proposição.

Como a conjunção é verdadeira quando P e Q são verdadeiros, sua tabela de verdade é:

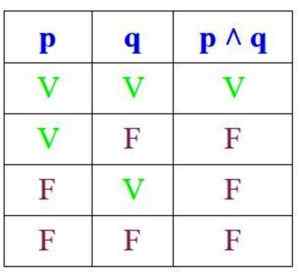
Por outro lado, em disjunção, a proposição é verdadeira se P e Q forem verdadeiros ou se pelo menos um deles for, mas é falso se ambos forem:

Pode atendê -lo: Permutações sem repetição: fórmulas, demonstração, exercícios, exemplos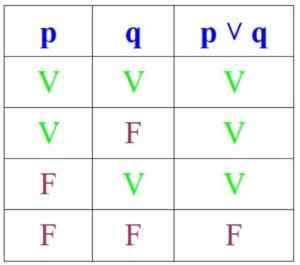

Agora, a negação transforma a verdade em falso e vice -versa. Nesse caso, os valores da verdade de ∼ (p ∧ q) e ∼ (p ∨ q) são o oposto dos valores da verdade (p ∧ q) e (p ∨ q):

E deve -se verificar se esses resultados são obtidos ao realizar as respectivas tabelas de verdade de (∼ P ˅ ∼ q) e (∼ P ˄ ∼ Q):

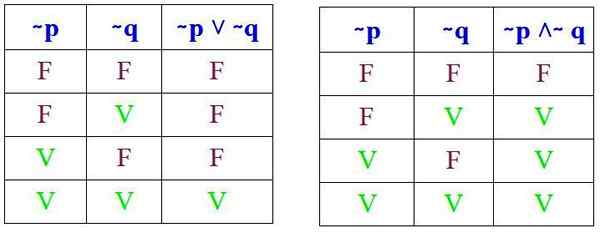
E, de fato, ao comparar as respectivas tabelas da verdade, observa -se que as leis de De Morgan são cumpridas. Agora dois exemplos de sua aplicação serão vistos.

Exemplo 1 resolvido 1

Aplique as leis de Morgan para encontrar a expressão equivalente de: ∼ (∼P ˅ ∼Q)

• Solução

A expressão dada é comparada ∼ (∼P ˅ ∼Q) com a lei de Morgan:

∼ (p ∨ q) ⇔ ∼p ∧q

E observa -se que a negação já está fora dos parênteses em ambos os casos; portanto, as instruções da lei são seguidas: ela se recusa ∼P, nega ∼q e o conector é alterado:

∼ (∼P ˅ ∼Q) ⇔ ∼ (∼P) ∧ ∼ (∼Q) ⇔ p ∧ q q

Exemplo 2 resolvido 2

Determine a expressão equivalente de ∼ [∼P ˄ ∼ (∼q)] ≡

• Solução

Primeiro, a negação ∼Q é simplificada:

∼ [∼P ˄ ∼ (∼Q)] ⇔ ∼ [∼P ˄ q]

Como já existe uma negação fora do suporte, a expressão resultante é comparada à lei de Morgan: ∼ (P ∧ q) ⇔ ∼P ∨q

Para resolver ∼ [∼P ˄ q], você deve negar ∼P, negar Q e alterar o conector:

∼ [∼P ˄ q] ⇔ ± (∼P) ∨ ∼Q ⇔ p ˅ ∼Q

Referências

1. Becerra, J.M.  Notas lógicas da UNAM.
2. Brilhante. Das leis de Morgan. Recuperado de: brilhante.org.
3. Tutoriais de eletrônicos. Pelo teorema de Morgan. Recuperado de: eletrônicos-tormales.Ws.
4. López, f. Introdução à lógica matemática. Recuperado de: youtube.com
5. Muñoz, c. Introdução à lógica. Recuperado de: sites.Ucm.é.