Fórmulas de Lei Hooke, Exemplos, Aplicações, Exercícios

O Lei de Hooke ressalta que a deformação experimentada por um objeto elástico é diretamente proporcional à força aplicada nele. A constante de proporcionalidade depende da natureza do objeto, de sua geometria e do material com o qual é fabricado.

Todos os materiais têm propriedades elásticas em maior ou menor grau, então cumprem a lei de Hooke sempre que retornam às suas dimensões originais, uma vez que a força cessa. Elastic Springs and Gumms são bons exemplos de objetos que cumprem a lei de Hooke, mas também os cabillas de aço que fazem parte de uma ponte.

figura 1. Lei de Hooke na primavera

Tomando como exemplo uma mola ou doca, para mantê -la esticada ou compactada, é necessário aplicar uma força cuja magnitude é f. De acordo com a lei de Hooke, a primavera experimentará uma deformação x:

F ∝ x

A constante de proporcionalidade, que, sendo uma primavera, é chamada rigidez da mola, É indicado como k, portanto:

F = k⋅x

Nas unidades do sistema internacional, a força vem em Newton (n) e a deformação em metros (m). Portanto, a constante de mola tem unidades N/m. A constante da mola representa a força que deve ser aplicada para deformá -la em 1 m de comprimento.

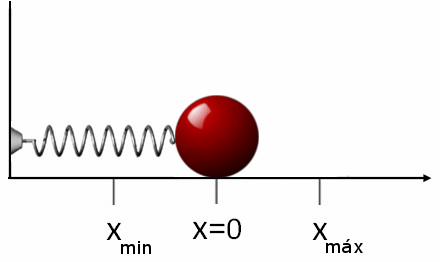Figura 2. Quando a mola é esticada, a força exercida no objeto é contrária. O mesmo acontece se a primavera encolher, neste caso, ele impulsiona o objeto no sentido oposto. Fonte: Wikimedia Commons.

Se depois de esticar ou comprimir a mola, ela será lançada, ela se moverá na direção oposta à força aplicada. Isso significa que, se o esticarmos, é comprimido e vice -versa. É por isso que forçar_R que Os exercícios da primavera é:

F_R = -k⋅x

O sinal negativo indica o que é dito: que a força se opõe ao deslocamento, então essa força é conhecida como Força restaurativa.

[TOC]

Fórmula e equações

A relação entre força e deslocamento em uma primavera foi descoberta por Robert Hooke (1635-1703), um físico inglês notável e conhecido por sua rivalidade com Isaac Newton. Hooke era um cientista versátil que se envolveu com sucesso em diferentes campos da ciência: mecânica, biologia, astronomia e arquitetura.

Figura 3. O físico inglês Robert Hooke, que não conhece retratos da época. Esta é uma reconstrução feita pela artista Rita Gerer em 2004 através de descrições deixadas por aqueles que conheceram o cientista. Fonte: Wikimedia Commons. Rita Greer / Fal.

Hooke percebeu que, se a força aplicada a um píer não é muito grande, a doca é proporcionalmente se deforma para forçar e, uma vez que a força desaparece, a primavera tem seu comprimento natural novamente.

Pode servir a você: magnetosfera da Terra: características, estrutura, gases

Dessa forma, a lei de Hooke graficamente tem a forma de uma linha reta, cuja inclinação é a constante de mola. A imagem a seguir mostra a força exercida na mola para esticá -la - ou comprimindo -a - dependendo da posição X. Observe que a força não depende da duração natural da primavera, mas em seu deslocamento.

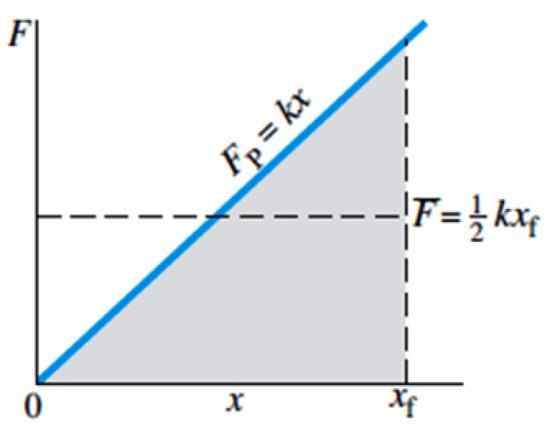Figura 4. Magnitude f da força necessária para esticar ou comprimir uma mola, dependendo da deformação x. Fonte: Giancoli, D. Física com aplicações.

A força média é indicada no gráfico por f com barra e é equivalente a ½ kx_F, onde x_F é a posição final da primavera.

Ambos a força exercida na primavera, e a força que ele exerce em um objeto amarrado a ele, são forças variáveis. Quanto mais você deseja esticar ou compactar até a primavera, mais força você deve se candidatar para poder alcançá -la.

Trabalho feito para esticar ou comprimir uma mola

Quando uma força é aplicada que deforma a mola, um trabalho que é armazenado na primavera é feito e que pode ser usado posteriormente.

O trabalho mecânico é definido como a área sob o gráfico da força f, dependendo da posição x. Para calcular o trabalho com que uma força variável f (x) faz ao mover um objeto da posição x₁ para posicionar x₂ A integral definida deve ser calculada:

No caso do trabalho necessário para trazer uma mola de sua posição de equilíbrio para a posição x_F É muito simples, já que a área a ser calculada é a do triângulo cinza sombreado da Figura 4, cuja fórmula é conhecida:

Área do triângulo = ½ base. altura

Portanto, o trabalho necessário é:

W = ½ x_F . (KX_F) = ½ K (x_F)²

E se você deseja calcular o trabalho necessário para trazer para a mola da posição x para a posição x_F, Seria equivalente a calcular a área do trapézio arranhado na Figura 5:

W = ½ K (x_F)² - ½ k x²

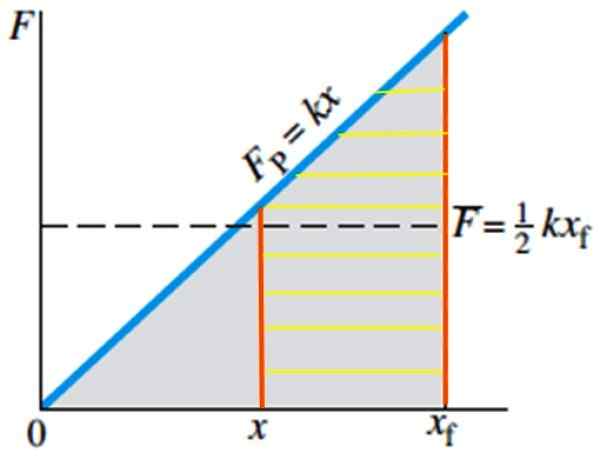Figura 5. O trabalho realizado para esticar a mola da posição X à posição XF equivalente à área de Rayada. Fonte: Giancoli, D. Física com aplicações.

Exemplos de molas

De acordo com a aplicação a que se destinam, as molas podem ser cilíndricas, cônicas, em espiral, com uma seção transversal circular (a mais comum), de seção quadrada ou retangular.

Pode atendê -lo: condutores elétricos

Uma classificação amplamente usada está de acordo com o tipo de esforço ao qual eles serão submetidos: há torção, flexão, compressão e molas de extensão. Estes últimos são usados ​​extensivamente e também há trabalho para tensão e compressão.

Mola de compressão

Um exemplo de primavera de compressão é o que é usado no brinquedo chamado POGO qualquer Saltoín Palo. Essas fontes armazenam uma energia bastante potencial quando compactadas e liberadas gradualmente ao retornar à posição de equilíbrio. Dessa maneira, os rebotes não são muito abruptos.

Figura 6. Pogo ou Saltoín Stick é baseado em uma mola de compressão. Fonte: Wikimedia Commons.

Extensão e molas de torção

A mola para spramps é o tipo de molas de extensão e é fabricada com curvas bem roladas, com dois ganchos nas extremidades. Eles são capazes de reter energia potencial suficiente, que mais tarde liberam quando alguém se levanta e começa a pular na tela, que também tem sua própria resposta elástica, como todos os materiais.

As molas de torção são muito comuns, porque servem para fazer grampos de roupas. Em vez de ganchos nas extremidades, eles se dobram em ângulo, para resistir às forças que tendem a exercer torção.

Figura 7. As fontes fazem parte de inúmeros mecanismos, como essas pinças de roupa. Fonte: Pxfuel.

Materiais para molas de fabricação

Os materiais mais adequados para fazer molas são aqueles com um Resistência final (Resistência final), ou seja, eles apoiam um grande esforço antes de quebrar. Também é conveniente que o material tenha um ponto de fluência alto, para que não perca suas qualidades elásticas com pequenos esforços.

As molas de uso industrial são fabricadas com ligas que incluem aço com alto teor de carbono, cobre, níquel e bronze.

Aplicações da lei de Hooke

Como as fontes têm a virtude de armazenar energia em potencial quando se estendem ou se compactam, elas são capazes de trabalhar movendo coisas como mecanismos.

Dessa maneira. As nascentes servem para:

-Vibrações de choque.

-Fabricar mecanismos retráteis: caneta, pinça pendurada, ganchos de cabelo.

-Faça primavera ou dinamômetros

E eles também fazem parte do mecanismo de:

Pode atendê -lo: circuito elétrico fechado

-Relógios.

-Trampolins.

-Bloqueios.

-Brinquedos.

-Armas.

-Medidores de agulha, por exemplo, o galvanômetro, usado para medir correntes, tensões e resistências.

Exercícios resolvidos

- Exercício 1

Uma força de magnitude 5 é aplicada.0 n em uma primavera, fazendo um comprimento de 3 alongamento.5 cm de seu comprimento natural.

a) Quanto é esticado quando a força aplicada é 7 n?

b) Encontre o trabalho realizado pela força aplicada para se estender até a primavera 3.5 cm de seu comprimento natural.

Solução para

Sabendo que a primavera é alongada 3.5 cm através da aplicação de 5.0 N podemos calcular sua constante:

k = f / x = 5.0 N / 3.5 cm = 1.43 N / cm.

Quando uma força de 7 n é aplicada, é obtido o seguinte trecho:

x = f / k = 7.0 N / 1.43 N/M = 4.9 cm

Solução b

O trabalho necessário para deformar uma mola é dado por:

W = ½ kx² = 0.5 x 1.43 N / cm x (3.5 cm)² = 8.76 n . cm = 8.76 n . 1 x10 ^-2 M = 0.0876 J.

- Exercício 2

Uma mola de massa desprezível e 10 cm de comprimento penduram de um suporte. Se uma massa de 2 kg estiver enforcada, a mola será esticada até atingir 15 cm. Calcular:

a) a constante de mola

b) o tamanho da mola quando uma massa de 3 kg é suspensa.

Solução para

Alongamento da primavera é x = 15 - 10 cm = 5 cm

Como o sistema está em equilíbrio estático, a força exercida pela mola quando o alongamento é direcionado verticalmente para cima, para compensar o peso, que é direcionado para baixo, então:

F_R = W → kx = mg

K = 2 x 9.8 n / 5 x10 ^-2 M = 392 N/m

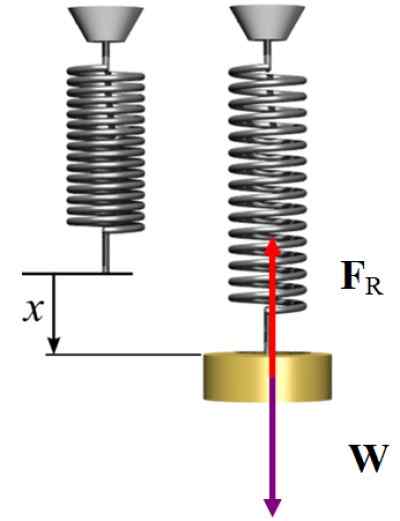Diagrama do corpo livre para o exercício resolvido 2. Fonte: Wikimedia Commons/F. Zapata.

Solução b

Quando um peso de 3 kg é suspenso, a nova força é w = 3 x 9.8 n = 29.4 n

Nesse caso, o trecho é:

x = mg /k = 29. 4 N / 392 N / M = 0.075 m = 7.5 cm

Referências

1. Bauer, w. 2011. Física para engenharia e ciências. Volume 1. Mc Graw Hill.
2. Blog de mecanismos criativos. Quatro tipos diferentes de molas. Recuperado de: CreativeMecanisms.com.
3. Figueroa, d. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dinâmico. Editado por Douglas Figueroa (USB).
4. Giancoli, d.  2006. Física: Princípios com aplicações. 6º. Ed. Prentice Hall.
5. Cavaleiro, r.  2017. Física para cientistas e engenharia: uma abordagem de estratégia.  Pearson.